初学深度学习——详解BP神经网络与反向传播算法推导过程

一.梯度下降优化算法

首先我们先来介绍一下什么是梯度，BP神经网络反向传播的过程就是对权值$w_{ij}$进行更新的的过程，而更新权值则离不开梯度的计算。
大学时我们学过怎样求函数 $y=f(x)$的极值。函数的极值点，就是它的导数$f^{\prime }(x)=0$的那个点。因此我们可以通过解方程$f^{\prime }(x)=0$，求得函数的极值点$（x_0,y_0）$。
不过对于计算机来说，它可不会解方程。但是它可以凭借强大的计算能力，一步一步的去把函数的极值点『试』出来。如下图所示：

首先，我们随便选择一个点开始，比如上图的$x_0$点。接下来，每次迭代修改的$x$为$x_1,x_2,x_3,$…，经过数次迭代后最终达到函数最小值点。
你可能要问了，为啥每次修改$x$的值，都能往函数最小值那个方向前进呢？这里的奥秘在于，我们每次都是向函数$y=f(x)$的梯度的相反方向来修改。
什么是梯度呢？翻开大学高数课的课本，我们会发现梯度是一个向量，它指向函数值上升最快的方向。显然，梯度的反方向当然就是函数值下降最快的方向了。我们每次沿着梯度相反方向去修改$x$的值，当然就能走到函数的最小值附近。之所以是最小值附近而不是最小值那个点，是因为我们每次移动的步长不会那么恰到好处，有可能最后一次迭代走远了越过了最小值那个点。步长的选择是门手艺，如果选择小了，那么就会迭代很多轮才能走到最小值附近；如果选择大了，那可能就会越过最小值很远，收敛不到一个好的点上。

按照上面的讨论，我们就可以写出梯度下降算法的公式:
$$X_{new}=X_{old}-\eta \nabla f(x)$$其中，$\nabla$是梯度算子，$\nabla f(x)$就是指$f(x)$的梯度。$\eta$是步长，也称作学习速率。
对于BP神经网络来说，每个结点之间的权值更新公式为：
$$w_{ji}\leftarrow w_{ji}+\eta {\delta }_j{x}_{ji}$$其中，是$w_{ji}$节点到节点的权重，$\eta$是一个成为学习速率的常数，${\delta }_j$是节点j的误差项，$x_{ji}$是节点i传递给节点的输入。
也就是说，如果要求出梯度，就要求出每个结点的误差项${\delta }_j$

二.反向传播算法与推导

反向传播算法（Back Propagation）

我们假设每个训练样本为$(x,t)$，其中向量$x$是训练样本的特征，$t$而是样本的目标值。如下图所示：

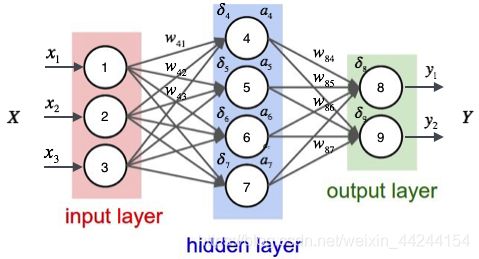
其中，$input$ $layer$表示样本的输入，有三个节点，我们将其依次编号为1、2、3，在上图中有三个样本的输入$x_1,x_2,x_3$，$hidden$ $layer$表示隐藏层，在上图中隐藏层有四个结点，编号依次为4、5、6、7，$output$ $layer$表示样本的输出，在上图中有两个样本的输出$y_1,y_2$。
那么，每个结点的误差项${\delta }_i$为：

·对于输出层结点$i$

$${\delta }_i=y_i(1-y_i)(t_i-y_i)$$其中，${\delta }_i$是节点$i$的误差项，$y_i$是节点$i$的输出值，$t_i$是样本对应于节点$i$的目标值。
举个例子，根据上图，对于输出层节点8来说，它的输出值是$y_1$，而样本的目标值是$t_1$，带入上面的公式得到节点8的误差项${\delta }_8$应该是：
$${\delta }_8=y_1(1-y_1)(t_1-y_1)$$

·对于隐藏层结点

$${\delta }_i=a_i(1-a_i)\sum _{k\in outputs}{w}_{ki}{\delta }_k$$其中，$a_i$是节点$i$的输出值，$w_{ki}$是节点$i$到它的下一层节点$k$的连接的权重，${\delta }_k$是节点$i$的下一层节点$k$的误差项。
例如，对于隐藏层节点4来说，计算方法如下：
$${\delta }_4=a_4(1-a_4)(w_{8}4{\delta }_8+w_{9}4{\delta }_9)$$最后，更新每个连接上的权值：
$$w_{ji}\leftarrow w_{ji}+\eta {\delta }_j{x}_{ji}$$其中，$w_{ji}$是节点$i$到节点$j$的权重，$\eta$是一个成为学习速率的常数，${\delta }_j$是节点$j$的误差项，$x_{ji}$是节点$i$传递给节点$j$的输入。
例如，权重$w_{84}$的更新方法如下：
$$w_{84}\leftarrow w_{84}+\eta {\delta }_8{a}_4$$类似的，权重$w_{41}$的更新方法如下：
$$w_{41}\leftarrow w_{41}+\eta {\delta }_4{x}_1$$而偏置项的输入值永远为1。
以上神经网络每个节点误差项的计算和权重更新方法。
显然，计算一个节点的误差项，需要先计算每个与其相连的下一层节点的误差项。这就要求误差项的计算顺序必须是从输出层开始，然后反向依次计算每个隐藏层的误差项，直到与输入层相连的那个隐藏层。这就是反向传播算法的名字的含义。
当所有节点的误差项计算完毕后，我们就可以根据$w_{ji}\leftarrow w_{ji}+\eta {\delta }_j{x}_{ji}$来更新所有的权重。

反向传播算法的推导

由于博客编写公式太过麻烦，下面我用图片手写公式来推导BP反向传播算法

1.观察上图，先进行正向前馈过程：

2.接下来是训练过程：

随机梯度下降法(Stochastic Gradient Descent, SGD)：

如果我们根据总误差批量处理来训练模型，那么我们每次更新的迭代，要遍历训练数据中所有的样本进行计算，我们称这种算法叫做批梯度下降(Batch Gradient Descent)。如果我们的样本非常大，比如数百万到数亿，那么计算量异常巨大。
因此，实用的算法是SGD算法。在SGD算法中，每次更新的迭代，只计算一个样本。也就是采用随机处理来处理单个样本。这样对于一个具有数百万样本的训练数据，完成一次遍历就会对更新数百万次，效率大大提升。由于样本的噪音和随机性，每次更新并不一定按照减少的方向。然而，虽然存在一定随机性，大量的更新总体上沿着减少的方向前进的，因此最后也能收敛到最小值附近。

3.求E对于各个参数的梯度

①对于输出层结点来说，$E$是$y_k$的函数，而$y_k$是$ne{t}_k$的函数，$ne{t}_k$是$w_{jk}$和$b_k$的函数，根据链式求导法则得：

这样，我们便推导出了输出层结点得误差项啦

②对于隐藏层结点来说，由链式求导法则对其进行拆分，转而求得隐藏层结点得误差项

参考资料：零基础入门深度学习(3) - 神经网络和反向传播算法