2D基本图形的Sign Distance Function (SDF)详解(下)
符号距离函数(sign distancefunction),简称SDF,又可以称为定向距离函数(oriented distance function),在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义:点在区域边界内部为正,外部为负,位于边界上时为0。
您可以在 2D基本图形的Sign Distance Function (SDF)详解(上)这篇文章里找到前1~9个基础2D几何图形的SDF~
10. 正五边形
代码:
/**
* 正五边形 1. 原点在中心点, 中心点到某一个顶点的向量沿y轴负半轴
* 2. r表示中心点到边的距离(不是到顶点的距离)
*/
float sdPentagon( in vec2 p, in float r )
{
// pi/5: cos, sin, tan, !!!注意,k仅作为一个数据的集合!
const vec3 k = vec3(0.809016994,0.587785252,0.726542528);
p.x = abs(p.x); // 左右对称
// 1. 先映射:同样是分为三部分,上部+右上+右下,都要映射到上部
// 将op在(-k.x, k.y)上投影,得到一个系数,若系数是正数说明p点在上部不用处理,被min(0.0, )滤去
// 若为负数说明在目标范围内,p加上1倍的系数*单位垂直向量就可以到达对称轴处
// 再加一倍就到达对称点处,因此下面要乘2,-=其实和上面说到的垂直向量的方向有关
p -= 2.0*min(dot(vec2(-k.x,k.y),p),0.0)*vec2(-k.x,k.y);
// 原先在右下部的区域,还得再映射一次,这里的min再滤去上部的部分
p -= 2.0*min(dot(vec2( k.x,k.y),p),0.0)*vec2( k.x,k.y);
// 2. 计算方便计算距离的区域
// 这里就是简单的考虑上部就好,因为右上映射上去后取值范围是(-,+),因此正负都要考虑,
// r*k.z是得到半边长,得到的最后的p是处于上部的点做一条垂线到五边形的上部水平边
p -= vec2(clamp(p.x,-r*k.z,r*k.z),r);
return length(p)*sign(p.y);
}
直接上图,这里真的忍不住安利一下 geogebra 这个几何绘图网站,超好用看下面这张动图就能一目了然算法的逻辑了。其中绿色的向量表示最终用来计算距离和内外的向量。首先是左右对称,然后我们就要开始经典的先找映射关系,再找到最好计算SDF的区域来计算。那么对于这样一个五边形最好计算的区域是哪里呢?肯定是下图处于上方的偏红色的部分,只需要比较P点的y坐标和参数r即可。那么其他两个区域呢?也就是下图中的蓝色和绿色区域,肯定是投影啦。蓝色区域内的点可以通过以动图中蓝色的直线为对称轴映射到红色区域,那绿色的部分呢?其实有不止一中办法,例如可以先映射到蓝色,再按之前的办法以蓝线为对称轴映射到红色,但是这样的话代码就会有判断语句,我们的iq大神使用了一种代码量更少的办法,那就是绿色区域一开始也随着蓝色区域对称过去,然后再根据图中绿色的直线再对称映射一次,这个第二次对称蓝色区域是不参加的,为什么它能够不参加呢?奥秘就是代码里面的min(xxx, 0.0),它能把超过该区域的部分给过滤掉。
虽然在之前正三角形的介绍里面也有用到对称操作,但那是直接给出了映射的结果,可以说就是按照以前高中数学的方式,先设对称后的点为(x', y'),然后用两个条件:对称前后两点连线的中点在对称轴上;两点连线和对称轴垂直。列出两条二元一次方程求解即可。但是在这里我们看到了一种更有几何风格的解法:P点沿着垂直对称轴的方向走,到达对称轴后,再继续前进一段相同的距离就到达了对称点了。所以代码里面的vec2(-k.x, k.y)其实是垂直于下图蓝色对称轴的单位向量,vec2(k.x, k.y)是垂直于红色对称轴的单位向量。前面乘2.0就是走两倍距离的意思。
11. 正六边形
代码:
/**
* 正六边形 1. 原点在中心点,有两条边与x轴平行
* 2. r表示中心点到边的距离(不是到顶点的距离)
*/
float sdHexagon( in vec2 p, in float r )
{
// -cos30, sin30, tan30, !!! 注意,k仅作为一个数据的集合
const vec3 k = vec3(-0.866025404, 0.5, 0.577350269);
p = abs(p); // xy轴对称,因此全部只看第一象限即可
// 观察图像可以看出我们选择的对称轴应该是(cos60, sin60)==(sin30, cos30)
// (-cos30, sin30)也就是k.xy,是与选择的对称轴垂直的单位向量
p -= 2.0*min(dot(k.xy,p),0.0)*k.xy;
// 下面同理
p -= vec2(clamp(p.x, -k.z*r, k.z*r), r);
return length(p)*sign(p.y);
}
理解了正五边形的对称映射之后。我相信再理解正六边形肯定不是难事。有一点需要注意的是,代码中的k是一个集合,前往别老看着k.x和k.y老觉得k是一个向量。当然它确实可以表示一个向量,但我觉得始终强调它是数据集合更好。(换我来写肯定是写成三个float啦)后面还有正的八边形也是相同的套路,我就不列出来了,确定好对称轴和它的垂直方向就可以解决这些正的n边形。
12. 六角星
代码:
/**
* 六角星 1. 原点在中心点,中心点到某个角的连线于y轴平行
* 2. r表示中心点顶点的距离的1/2
*/
float sdHexagram( in vec2 p, in float r )
{
// -cos60, sin60, tan30, tan60
const vec4 k = vec4(-0.5,0.8660254038,0.5773502692,1.7320508076);
p = abs(p);
// 大体如上,需要注意的是这次的两次对称实际上互不干扰,我们最终要映射到是一条水平边
// 在六角星中,每个象限内由三条边,而水平边刚好在中间,因此两次对称不干扰(min()都会过滤掉对方)
// k.xy表示下图红线的垂直单位向量, k.yx表示下图蓝线的垂直单位向量
p -= 2.0*min(dot(k.xy,p),0.0)*k.xy;
p -= 2.0*min(dot(k.yx,p),0.0)*k.yx;
p -= vec2(clamp(p.x,r*k.z,r*k.w),r); // 注意水平边的起止范围
return length(p)*sign(p.y);
}
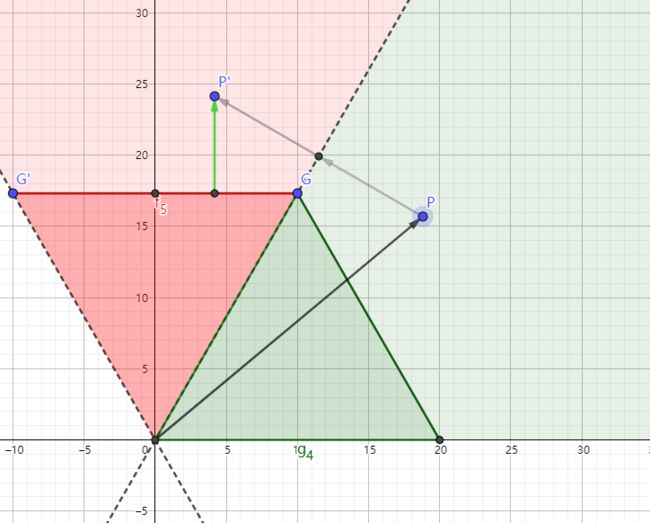
这个其实是后面那一个函数前的开胃小菜,它虽然也是n角星,但用的方法和前面的正多边形是一样的,在第一象限我们找到的比较容易计算SDF的区域是下图的红色区域,所以蓝色区域和黄色区域都分别按照各自的对称轴对称即可。

13. n角星
代码:
/**
* N角星 1. 原点在中心点,中心点和凸角的连线在x轴上
* 2. r表示中心点到某个凸角的距离
* 3. n表示几个凸角,m表示角的尖锐程度,具体是pi/m = 凹角(向内)的一半,
* 例如 m=2,凹角的一半是九十度也就是凹角是一百八,就是不凹,是正多边形
* 1
float sdStar(in vec2 p, in float r, in int n, in float m)
{
// 先计算所需的角度正余弦数据
float an = 3.141593/float(n); // 某两个相邻角与原中心点连线形成的角度的一半
float en = 3.141593/m; // 凹角的一半
// 分别计算正余弦
vec2 acs = vec2(cos(an),sin(an));
vec2 ecs = vec2(cos(en),sin(en)); // 特殊地,当ecs=(0, 1)时,表示的是正多边形
// 1. 映射:
// (这里对iq大神的原代码进行了小修改,只是最终方向有所改变而已)
// 原句: float bn = mod(atan(p.x,p.y), 2.0*an) - an;
float bn = mod(atan(p.y,p.x)+an, 2.0*an) - an;
// 原op的长度保持不变,方向调整到bn方向
p = length(p)*vec2(cos(bn),abs(sin(bn)));
// 2. 计算最短距离和符号
p -= r*acs;
p += ecs*clamp(dot(p, -ecs), 0.0, r*acs.y/ecs.y);
return length(p)*sign(p.x);
}
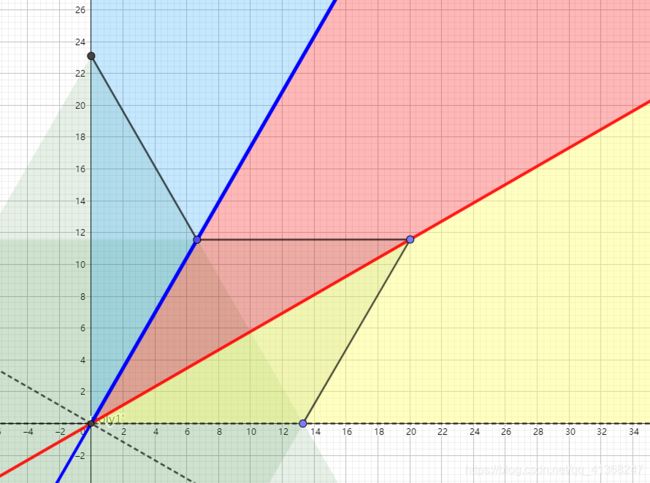
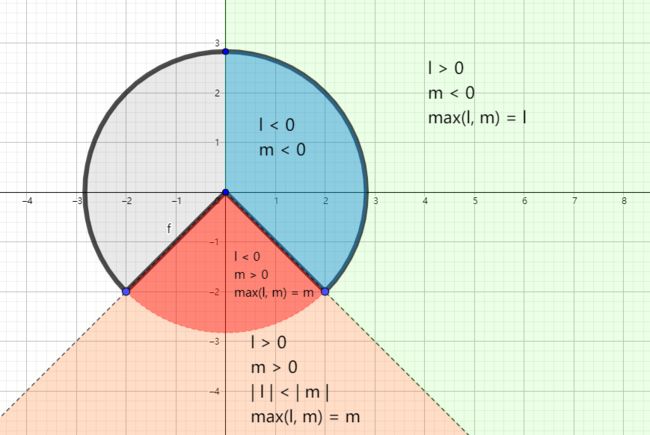
解决问题时如果找准了角度那么经常可以迎刃而解。例如n角星,我们知道它是一个很规则的图形,不论n取几(肯定大于2),它都可以被平分为n份,平分的方法如下图所示(PS:当然还有另一种平分的方法,那就是每个角占一份,那样也是可以的,这里先不讨论那种情况了)。我们认为其中最容易计算SDF的是平行于x轴的那一部分,其他部分都可以通过投射到这个区域来进行计算。但是由于我们的n可能取一个很大的值,现在就不能做各种对称了,得找一个更加通用的方法。没错其实就是旋转,float bn = mod(atan(p.y, p.x)+an, 2.0*an) - an;这句看似复杂,其实做就是计算出一个新的OP’和x轴的夹角,这一步取模很巧妙,先加an度再取模,相当于把每个部分角度都限制在了[0, 2*an]里面,这里说的“每一部分”,就是上文和下图中的n等份个小块。由于这些小块也是轴对称的,那我们可以把角度再减去一个an,相当于顺时针旋转,就可以得到下图这样的位置,也就是用x轴平分了一个小块。这样的好处是我们只需要考虑x轴上方的情况就可以了。p = length(p)*vec2(cos(bn), abs(sin(bn)));注意这个abs就是沿x轴翻转了上去,这句话相当于把每个P点都映射到了一个x轴上方的三角区域内。观察下图的 P’ 点。
映射做好了,接下来就是计算SDF了,在图中,按照EP’在向量ecs上投影的取值,我们将区域划分为红色、黄色和蓝色三块。在红色区域里,图形上里P’点最近的是凹角顶点,黄色区域内则是P’到边的距离最短,而蓝色区域内是凸角点到P’的距离最短。同样的投影→限制在范围内→相加,即可求得最终的SDF。如果理解有困难,下面列出了代码和动图上的点的对应关系:
- P:
P - P’:
p = length(p)*vec2(cos(bn), abs(sin(bn))); - Q:
ecs*clamp(dot(p, -ecs), 0.0, r*acs.y/ecs.y); - N:
p + ecs*clamp(dot(p, -ecs), 0.0, r*acs.y/ecs.y); - 绿色向量[区间1/2/3]:
示意最短向量,实际上是将N平移后得到

PS: 写博客的过程中利用 geogebra 进行图形绘制,惊讶地发现居然能进行一些简单的编程,例如上图的P’点我就是将iq大神的代码翻译为数学语言然后在这个网站里面能进行精彩的演示,也太棒了吧o( ̄▽ ̄)ブ 不仅能很方便地做垂线、平行、画多边形,还能动态计算和显示,爱了爱了~
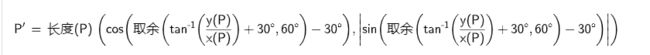
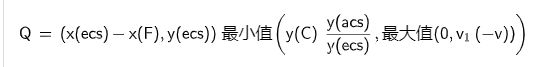
14. 梯形
代码:
/**
* y轴对称的梯形 1. 原点在中心点(x=底的一半,y=高的一半处)
* 2. r1:下底的一半,r2:上底的一半, h:高的一半
*/
float sdTrapezoidY( in vec2 p, in float r1, float r2, float he )
{
// 原点指向右上角顶点的向量
vec2 k1 = vec2(r2,he);
// 右腰
vec2 k2 = vec2(r2-r1,2.0*he);
// 左右对称图形,只看右边
p.x = abs(p.x);
// 同样是三块区域,根据距离最短点的位置,划分为:上底部分+下底部分+腰部分
// 上底下底可以统一处理,即ca,比较容易判断,在y负半轴的点x减去下底长度
// y上半轴的点x减上底,小于0说明x轴投影在内部,此时最小距离就是p.y-h
// 似乎这样可以直接返回了,其实不然,在梯形外部的点确实可以直接返回p.y-h但是在梯形内部的点
// 我们不清楚它是距离底近还是距腰近(梯形外部的点可以很快判断),所以不能就此返回,最后面要比较
// 1. 计算与(上/下)底的距离
vec2 ca = vec2(max(0.0,p.x-((p.y<0.0)?r1:r2)), abs(p.y)-he);
// 当然,确定的在梯形外部的上底部分和下底部分,可以直接返回
// if(ca.x<=0.0 && ca.y>0.0) return ca.y;
// 2. 计算和腰的距离
vec2 cb = p - k1 + k2*clamp( dot(k1-p,k2)/dot2(k2), 0.0, 1.0 );
// 内外判断
float s = (cb.x < 0.0 && ca.y < 0.0) ? -1.0 : 1.0;
// 取最小的
return s*sqrt( min(dot2(ca),dot2(cb)) );
}
前面确实说得有点太啰嗦了,那后面的几个图形就只讲重点吧。细心的读者可能也发现了,目前为止我们将的图形都是直线段和圆弧的组合体,大多数时候使用的都是找对称关系然后映射,映射完投影到某一条直线。如果直观上无法判断投影到哪一条直线是最短距离的话,最多就都分别计算出来,然后在后面比较一下即可。就像我们现在在说的梯形。梯形左右对称,计算P点到腰和到某一条底的距离,再取较小的那个值即可。其实这一小节需要解释的问题是,如果你看过iq大神再shadertoy上关于梯形SDF的演示,你就会看到另外一个更加一般的梯形的SDF,也就是不关于Y轴对称的。说实话他写的比较绕,直观上并非我我们前面提到的先对P点进行平移旋转操作,再直接调用Y轴对称的版本,而是直接将各种量进行一个等价的替换,相当于重新构建了一个坐标系,然后再重写一遍Y轴版本的函数。实际上也等价于先平移旋转再计算Y对称,只不过写得很有迷惑性,我将解释写在注释里(如果嫌太绕其实不看也可以)
代码:
/**
* 任意方向的梯形 1. 原点并不指定
* 2. a表示下底中心点,b上底中心点,ra是下底的一半长度
*/
float sdTrapezoid( in vec2 p, in vec2 a, in vec2 b, in float ra, float rb )
{
// 首先还是先计算
float rba = rb-ra; // 两半底长度的差
float baba = dot(b-a,b-a); // 高的长度的平方,重要
// ap需要注意,对照Y轴版本,其实这个就是op
float papa = dot(p-a,p-a);
// 此处是理解的关键,paba表示的 pa在高ba上的投影的长度占ba长度的比例,范围[0,1]
// 这个量在下面会经常和0.5比较,因为我们上面的Y轴对称版本里面的h其实是高的一半
// paba在下面出现时,我们可以认为它就是上面Y对称版本的p.y
// 当然 paba*sqrt(baba)才是ap在ab上的投影的实际长度,最后一步的时候才会乘此baba
float paba = dot(p-a,b-a)/baba;
// 同样分为两段,先计算和底的距离再计算和腰的距离,仔细观察会发现和Y版本一模一样,只是原来的p.y, p.x被替换了
// 上面我们说 paba可以看作Y版本的p.y,那么这一步就是计算Y版本的p.x
// 就是勾股定理,斜边是pa,一条直角边是pa在ba(也就是高)上的投影,那么画图我们就能发现,得到的其实是p点距离ba的垂线的长度,
// 至此其实我们已经相当于构建了一个新的坐标系,新坐标系里面的y轴是梯形的高,也就是ba
// x轴是垂直与y轴的,下面得到的x其实是p点在新x轴上投影的长度,我们视为新x,地位相当于Y版本的p.x
float x = sqrt( papa - paba*paba*baba );
// 与Y版本相似,当然我们说将paba视为前面的p.y其实不那么准确,paba-0.5才是视为前面的p.y
// 原因是两个坐标系选择的不同,新坐标系的原点在下底的中点,而Y版本中原点在梯形的中心点,
// 因此两个坐标系的y轴相对于梯形图像可以视为差了半个高的长度,所以paba-0.5才是视为前面的p.y
float cax = max(0.0,x-((paba<0.5)?ra:rb));
float cay = abs(paba-0.5)-0.5;
// k是腰长的平方
float k = rba*rba + baba;
// 也和Y版本一样,k就相当于dot2(k2)
// 原来的(k1-p)现在是:(x-ra, paba*sqrt(baba)), 原来的右腰k2现在是(rba, sqrt(baba))
// 点乘即右下底顶点指向P点的向量在腰上投影的长度所占腰长比例
float f = clamp( (rba*(x-ra)+paba*baba)/k, 0.0, 1.0 );
// 例如f==1时,cbx = x-ra-rba = x-rb, cby = paba - 1.0(这种情况paba肯定>1),这两个分量就表示p点到腰的垂线(反向)
float cbx = x-ra - f*rba;
// 这里的cby和上面的cay一样只是一个比例,需要乘baba才是真的距离
float cby = paba - f;
float s = (cbx < 0.0 && cay < 0.0) ? -1.0 : 1.0;
return s*sqrt( min(cax*cax + cay*cay*baba, // 注意乘baba,即高的长度
cbx*cbx + cby*cby*baba) );
}
15. 扇形
代码:
/**
* 扇形 1. 原点在圆心处,图形以y轴为对称轴
* 2. r半径, c是单位向量,扇形右半边界方向
*/
float sdPie( in vec2 p, in vec2 c, in float r )
{
// 对称
p.x = abs(p.x);
// 1.计算与弧的部分的距离
float l = length(p) - r;
// 2.与直线段边界的距离
float m = sign(c.y*p.x-c.x*p.y) * length(p-c*clamp(dot(p,c),0.0,r));
// 3. 比较
return max(l,m);
}
这个很好理解,唯一可能有问题的就是最后一句为何是max(),不是最短距离吗?其实应该结合图形来说。蓝色区域内由于两个值都小于零,那么max其实就是选绝对值最小的。绿色区域固定是l, 红色区域固定是m,因此max是没问题的。只怪程序过于追求简短,可读性不佳…( _ _)ノ|否则这里多些几个判断语句会更容易理解一点。

16. 圆弧
代码:
/**
* 弧 1. 原点在圆心处
* 2. sca表示弧的中心点和原点连线的单位向量,主要用于旋转
* 3. scb表示原点和右端点的圆心的连线的单位向量
* 4. ra表示原点到一个端点圆心的距离,rb表示端点圆的半径,也就是弧的宽度的一半
*/
float sdArc( in vec2 p, in vec2 sca, in vec2 scb, in float ra, float rb )
{
// 先旋转到可以左右对称的角度
// 注意,默认是sca表示pi/2,因此旋转矩阵的角度是:sca角度-pi/2(若sca传入pi/2,那实际上旋转0°)
// cos(x - pi/2) = sinx sin(x - pi/2) = -cosx
// 右乘的旋转矩阵 [cosθ, sinθ ] [sin, -cos]
// [-sinθ, cosθ] = [cos, sin]
p *= mat2(sca.y,-sca.x,sca.x,sca.y);
p.x = abs(p.x);
// k = p*cosθ
float k = (scb.y*p.x>scb.x*p.y) ? dot(p.xy,scb) : length(p.xy);
return sqrt( dot(p,p) + ra*ra - 2.0*ra*k ) - rb;
}
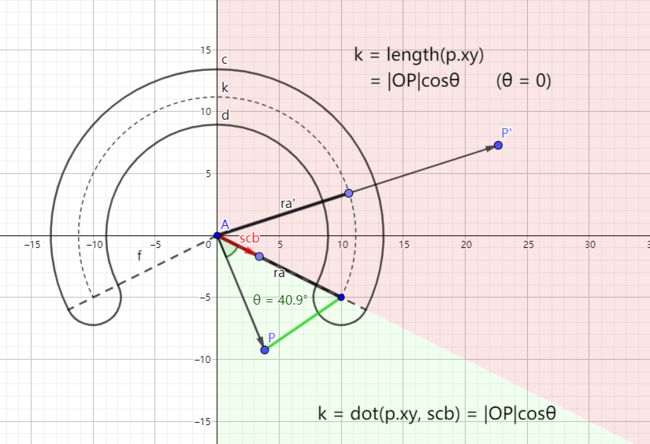
由于默认的图形没要求Y轴对称,所以一开始要先旋转,这里原代码用的是右乘的旋转矩阵,留心一下。然后分两个区域,得到k,最后使用余弦定理再减去圆弧宽度的一半即可。红色区域内虽然OP和ra重合不能组成三角形,但是不影响余弦定理的发挥。

17. Vesica (该咋翻译呢……)
代码:
/**
* Vesica: 1. 实际上是一个圆心在x轴正半轴上的圆,求其关于y轴的镜像,两部分之和
* 2. r表示圆的半径,d表示圆心与y轴的距离
* 为使图形看起来正常(联通),d的取值范围应该是(-r, r)
*/
float sdVesica(vec2 p, float r, float d)
{
p = abs(p); // 对称
// (0, b)是两圆的上交点
float b = sqrt(r*r-d*d);
// 分为两个部分,一个是最短距离点在圆弧上,一个是该最短距离点在(0, b)处,
// 判断方法是看op在向量(-d, b)的左边还是右边,左边(逆时针)则取(0,b)点,否则取弧
return ((p.y-b)*-d>p.x*b) ? length(p-vec2(0.0,b))*sign(-d) // 与(0, b)点(两圆交点)距离
: length(p-vec2(d,0.0))-r; // 与圆心距离
}
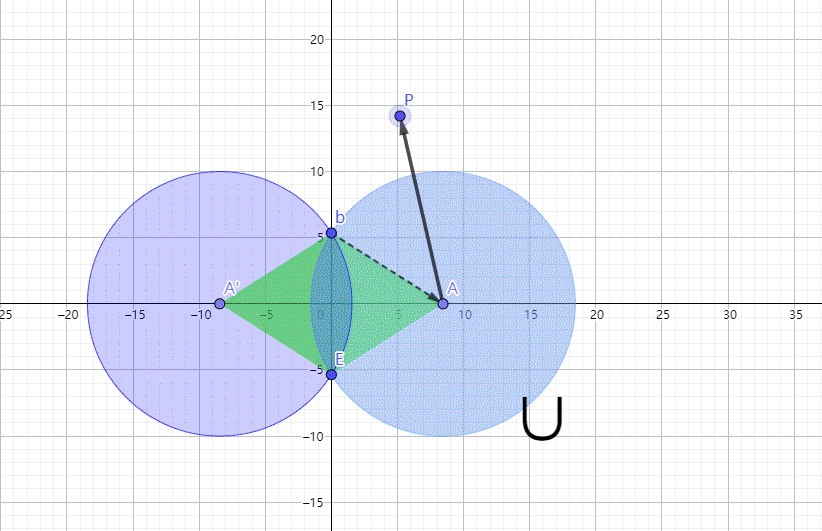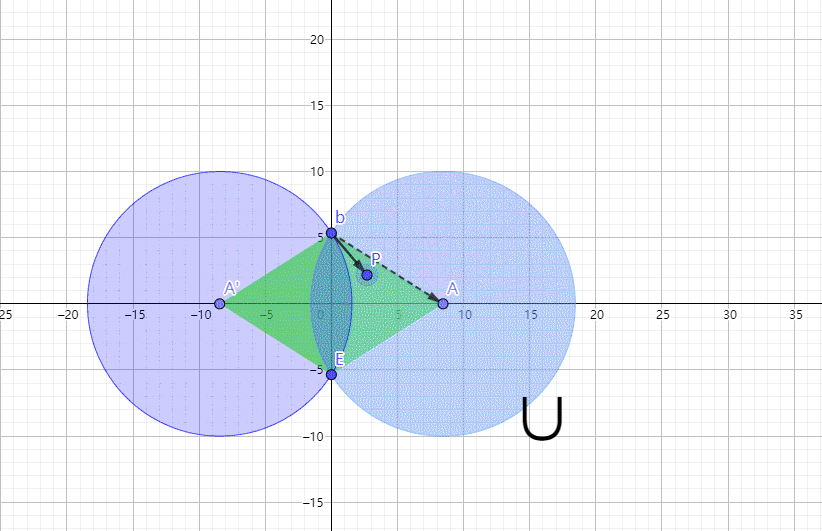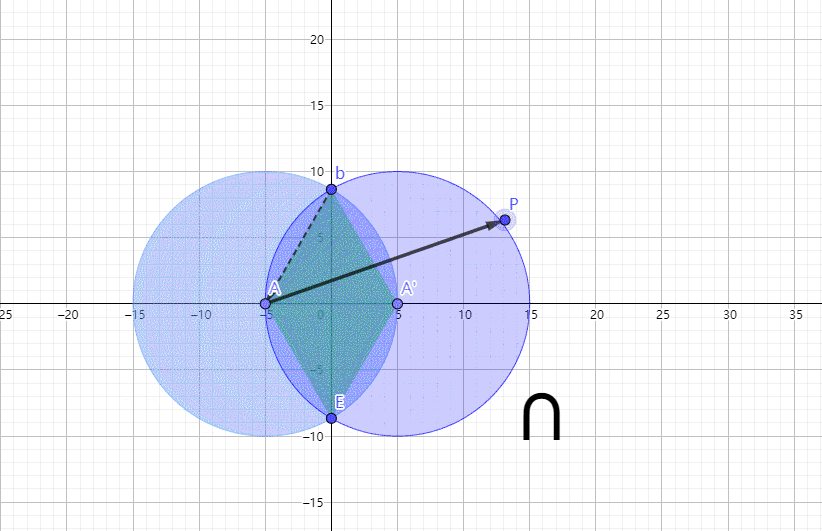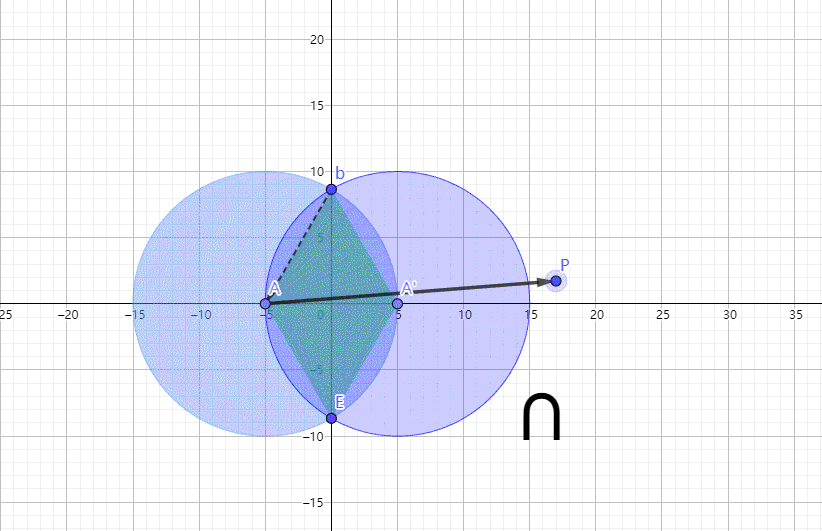
说白了就是俩圆互相融合,d表示圆心与y轴的距离,可以为负数。由于绘图软件还不是那么熟练,只能用右下角的符号提示下是取两个圆的并还是交。d>0是并,就是下图点A的坐标。随着d正负的改变,图形上与P点最短距离的点的判断方式也在改变。


18. 十字形
代码:
/**
* 十字 1. 原点在十字中心
* 2. 十字型由两个相同的长方形垂直组成
* b.x表示长方形长的一半,b.y表示宽的一半,若b.x==b.y则最终是一个正方形图形
* 3. r是最终距离的偏移量,不影响整体计算(可以通过调节r得到更漂亮的图形)
*/
float sdCross( in vec2 p, in vec2 b, float r )
{
// 四象限对称
p = abs(p);
// 关于直线y=x对称
p = (p.y>p.x) ? p.yx : p.xy;
// 假设十字横着的长方形右上角点a, 那么oa就是向量b
// q是从点a指向点p的向量
vec2 q = p - b;
// 三句话实现了五个区域的计算
float k = max(q.y,q.x);
vec2 w = (k>0.0) ? q : vec2(b.y-p.x,-k);
return sign(k)*length(max(w,0.0)) + r; // r调节最终结果
}
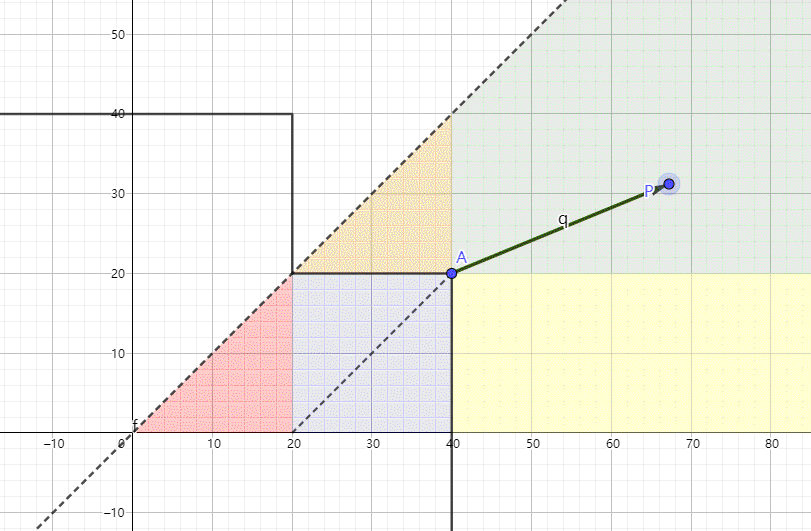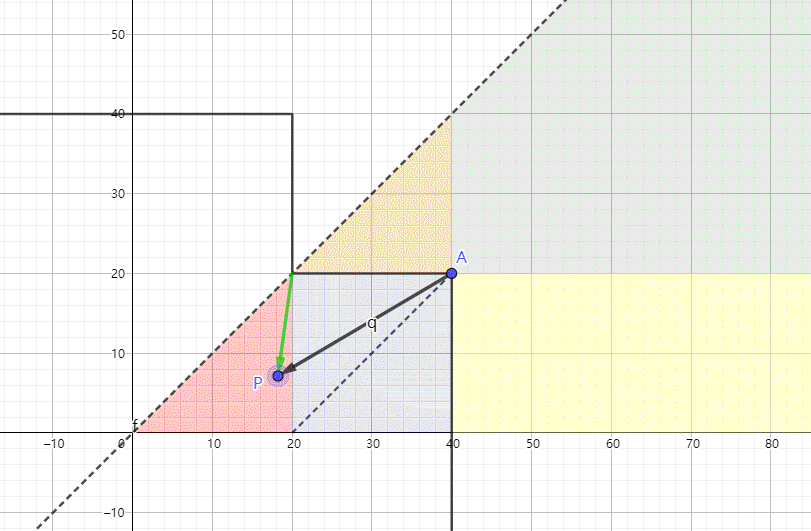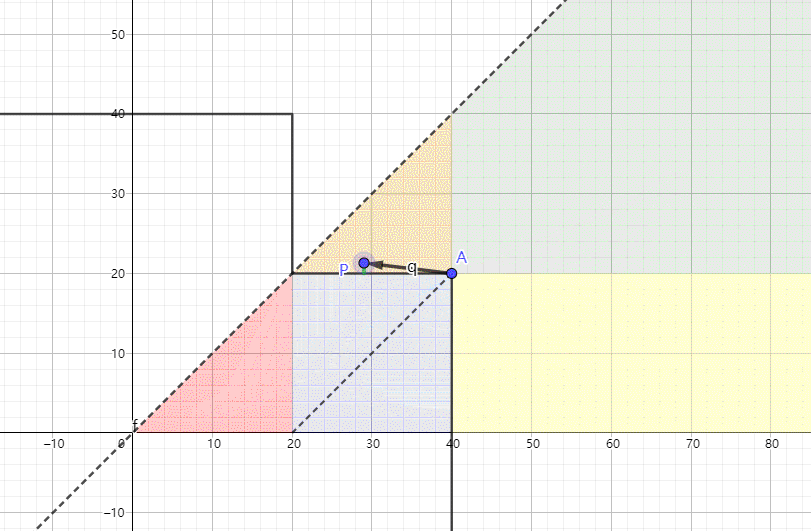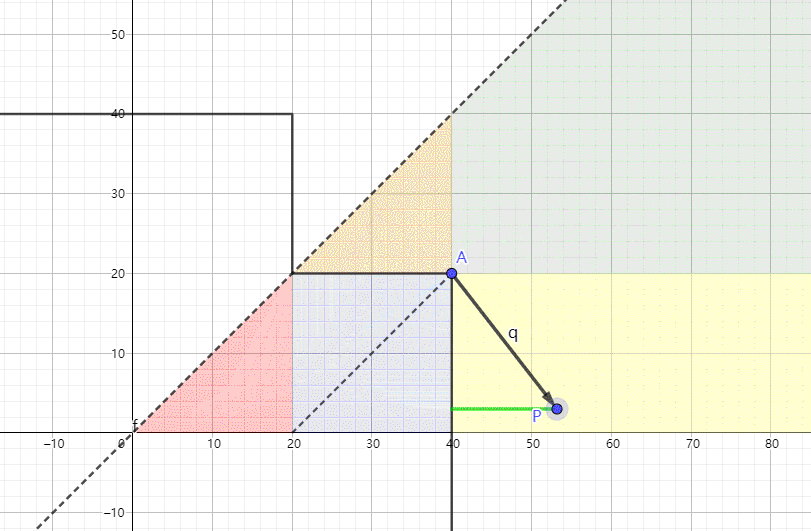
我觉得理解十字的SDF并不难,就五个区域嘛,如下图所示。右边的四个区域与长方形的SDF计算方法一致,只是多了一个左边的三角形区域而已。但是iq大神能将代码写得如此简短确实是厉害的(换做我早就五个if语句安排上了)

19. 叉
代码:
/**
* 叉 1. 原点在叉的中心,是两条与x轴角度分别为45°和-45°的椭圆/线条组合而成
* 2. w是叉的长度,r是宽度,r只需要最后调节即可
*/
float sdRoundedX( in vec2 p, in float w, in float r )
{
// 四个象限对称
p = abs(p);
// 投影到(1, 1)
return length(p-min(p.x+p.y, w)*0.5) - r;
}
这个比较简单,就是计算第一象限内一条与x轴夹角为45°的线段的SDF,然后分别根据x轴、y轴对称就好啦。可能比较有迷惑性的是这个0.5(不怕丢人,我当时瞧这个0.5瞧了好久也未解其妙)。其实,假设我们选取的向量是oa = (a, a), 投影占oa长度的比例:k = dot(op, oa)/(|oa|*|oa|) => dot(op, oa)/2a^2, op - k*(a, a)就表示点p到直线y=x的距离,所以这个*0.5其实就是除以2,归根结底就是因为1/(tan45°)^2 = 0.5。代码里面的式子相当于:
return length(p- vec2(1.0, 1.0)*clamp(dot(p, vec2(1.0/2.0, 1.0/2.0)), 0.0, w)) - r;
是为了方便选取的oa是(1, 1)而已,如果选择的是单位向量,则应该写成下面这样,化简结果是完全一样的。
const float sqrt2_2 = sqrt(2.0)/2.0;
return length(p- vec2(sqrt2_2, sqrt2_2)*clamp(dot(p, vec2(sqrt2, sqrt2)), 0.0, w/sqrt2_2)) - r;
20. 多边形
代码:
/**
* 多边形, N是确定的,GLSL里面不支持动态数组,v是各顶点的坐标的数组
*/
float sdPoly( in vec2[N] v, in vec2 p )
{
const int num = v.length();
float d = dot(p-v[0],p-v[0]);
float s = 1.0;
for( int i=0, j=num-1; i<num; j=i, i++ )
{
// 计算p点和每条边的最短距离
vec2 e = v[j] - v[i];
vec2 w = p - v[i];
vec2 b = w - e*clamp( dot(w,e)/dot(e,e), 0.0, 1.0 );
d = min( d, dot(b,b) );
// 通过缠绕数的奇偶规则来判断内外
bvec3 cond = bvec3( p.y>=v[i].y, p.y<v[j].y, e.x*w.y>e.y*w.x );
if( all(cond) || all(not(cond)) ) s*=-1.0;
}
return s*sqrt(d);
}
不规则的多边形计算距离只有比较暴力的方法,那就是计算点P与每条边的最短距离然后求最小值。但是重点是判断内外,这里用到的是缠绕数的奇偶-规则(参考博文):
“ 从任意位置p作一条射线,若与该射线相交的多边形边的数目为奇数,则p是多边形内部点,否则是外部点。”
程序里选择的射线是从p点出发,方向指向x轴负方向。这里有三个判定条件,有两个作用:前两个判定是否经过此射线,后一个判断是否在p点沿x轴负方向。 当一条边穿过此射线所在直线时,它方向可以向上或向下,向上的话前两个判定条件取负,若该边在p点的右边(x正方向)那么第三个条件此时取正,则该边不会影响结果,这条向上的边是在p点左边时,条件三才取负,此时才能算作射线穿过的边。当然这里面很多方向都不是固定的,比如选择射线方向是x轴正方向,那么第三个判定条件直接改为e.x*w.y < e.y*w.x;即可,不影响结果。可能有点违反直觉,居然取反也可以,其实最终影响结果的不是条件三的正负,而是条件三和前两个条件符号相同的次数,只要次数相同就不会影响结果了。前两个判定条件当然也可以改,只要它们两个的大于小于符号同时取相反就可以。 因为下面if里面的判定条件包含了全负和全正的情况。

21. 椭圆
代码:
// ab.x 表示长轴长度,ab.y表示短轴长度
float sdEllipse( in vec2 p, in vec2 ab )
{
p = abs(p); if( p.x > p.y ) {p=p.yx;ab=ab.yx;}
float l = ab.y*ab.y - ab.x*ab.x;
float m = ab.x*p.x/l; float m2 = m*m;
float n = ab.y*p.y/l; float n2 = n*n;
float c = (m2+n2-1.0)/3.0; float c3 = c*c*c;
float q = c3 + m2*n2*2.0;
float d = c3 + m2*n2;
float g = m + m*n2;
float co;
if( d<0.0 )
{
float h = acos(q/c3)/3.0;
float s = cos(h);
float t = sin(h)*sqrt(3.0);
float rx = sqrt( -c*(s + t + 2.0) + m2 );
float ry = sqrt( -c*(s - t + 2.0) + m2 );
co = (ry+sign(l)*rx+abs(g)/(rx*ry)- m)/2.0;
}
else
{
float h = 2.0*m*n*sqrt( d );
float s = sign(q+h)*pow(abs(q+h), 1.0/3.0);
float u = sign(q-h)*pow(abs(q-h), 1.0/3.0);
float rx = -s - u - c*4.0 + 2.0*m2;
float ry = (s - u)*sqrt(3.0);
float rm = sqrt( rx*rx + ry*ry );
co = (ry/sqrt(rm-rx)+2.0*g/rm-m)/2.0;
}
vec2 r = ab * vec2(co, sqrt(1.0-co*co));
return length(r-p) * sign(p.y-r.y);
}
其实从这里开始包括后面的Parabola和Quadratic Bezier都因为时间原因(其实还有能力原因)这里暂时没有做解析,以后有机会再补上吧。不过椭圆的部分其实还是有去了解过,计算平面内任意一点到给定椭圆的最短/最长距离,一直有这方面的研究。一开始还以为这是高中数学问题,后来发现常规思路做法需要解四次方程,超了高中的纲。有兴趣的同学可以读一下这篇论文: DistancePointEllipseEllipsoid,有提到怎样通过编程解决这个问题,2维3维都有。那在这里,iq大神给出了2维椭圆的SDF方程,还标记为 “exact” 看来应该也是没啥大问题。除此之外内,还给出了两个近似的计算方法,适用于2D和3D。其实就是简单地将一个椭圆视为一个圆在x方向和y方向上压缩后得到的图形(但是我们知道它并不是)。两种近似算法的讨论可以参考:iq大神自己的文章,这里我也稍微谈一下,第一种近似方法何其改进型开头的做法都是一样的,那就是将坐标系进行压缩,相当于将原来的坐标系的x轴单位变成r.x,即长轴的一半, y轴单位变成r.y,即短轴的一半。那么在新坐标系下椭圆就相当于一个单位圆了,直接求圆的sdf即可。问题是应该怎么样变回去,其实我们知道我们刚才的缩放是是各向异性的,圆是各向同性,我们从一个各向异性的椭圆用各向异性的比例缩小到各向同性的单位圆,放大回去的时候当然也应该是各向异性的操作。具体缩放的逆操作应该乘多少,和p点坐标有关,若p点在x轴上,则应该乘r.x,若在y轴上则应该乘r.y。当然这是理论上的,第一种近似方法比较粗暴,使用了一个固定的缩放系数min(r.x, r.y),这当然是不太精确的。于是在其改进型了,作者将这个系数变成了k1/k2,iq大神解释为:
A simple way to improve the previous bound is to divide by the length of its gradient. After some math on paper and nice rearrangement, one gets to this.
很遗憾我没能猜出作者纸上写的是什么内容,不过可以从其他的角度分析一下,改进的方向就是让系数可以随着p点位置的改边而变化。那其实我们也可以写一个系数:r.y+(r.x-r.y)*cos(r.y/r.x)这个系数可以说是会比第一个版本好一点,但是仍然不够精确吧。但是我们得到的启发是可以用点(r.x, 0)和(0, r.y)来判断系数选择得如何,从这个角度来看k1/k2就是一个不错的系数。总之,如果您有什么想法,或者知道iq大神为什么使用这个系数k1/k2作为改进型的参数,欢迎不吝赐教~
float sdbEllipsoidV1( in vec2 p, in vec2 r )
{
float k1 = length(p/r);
return (k1-1.0)*min(r.x,r.y);
}
// 改进型
float sdbEllipsoidV2( in vec2 p, in vec2 r )
{
float k1 = length(p/r);
float k2 = length(p/(r*r));
return (k1-1.0)*k1/k2;
}
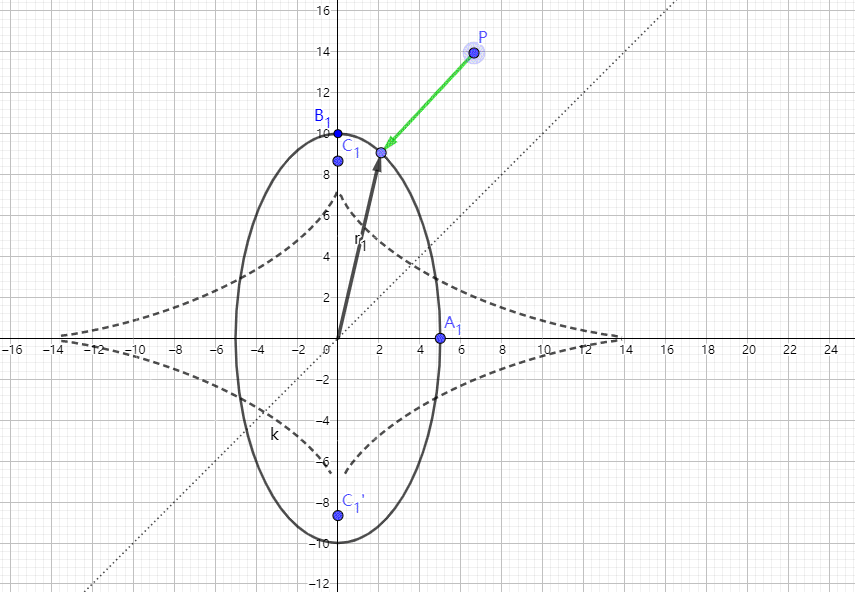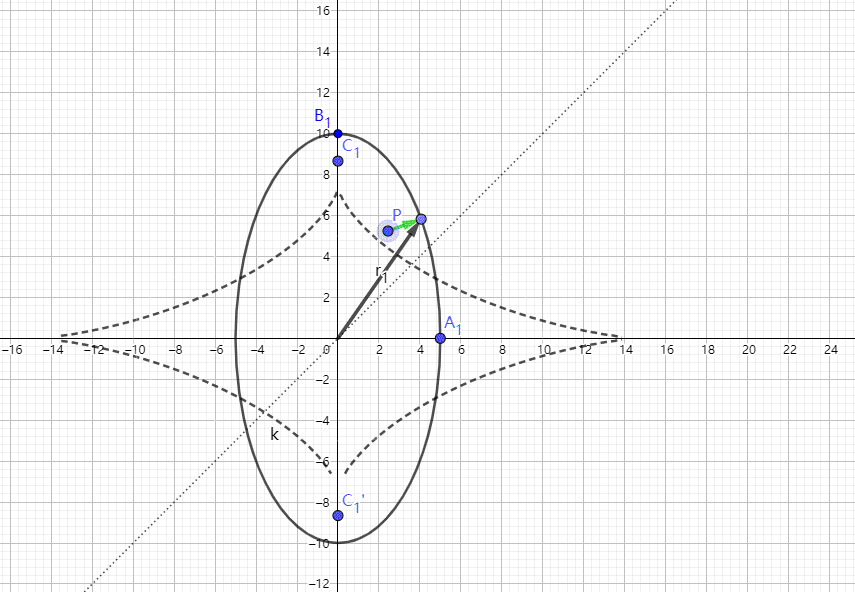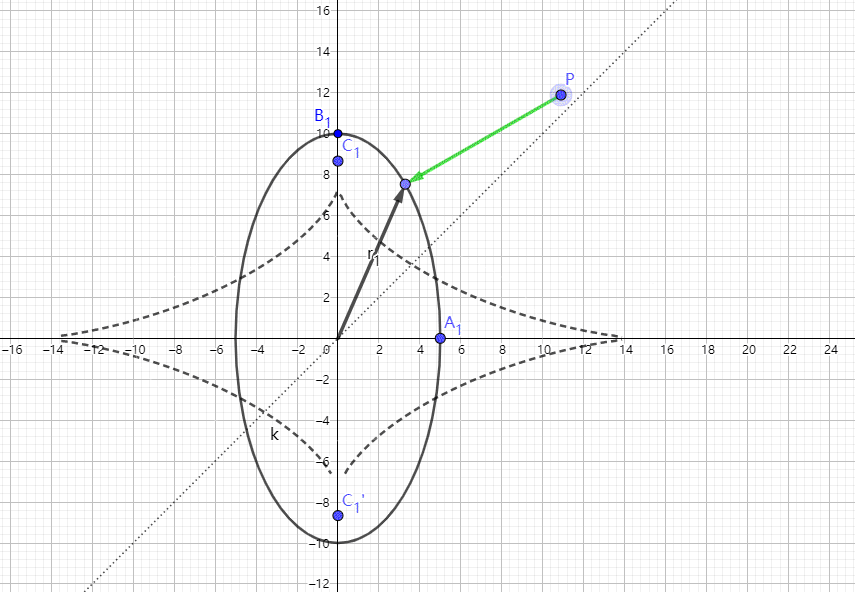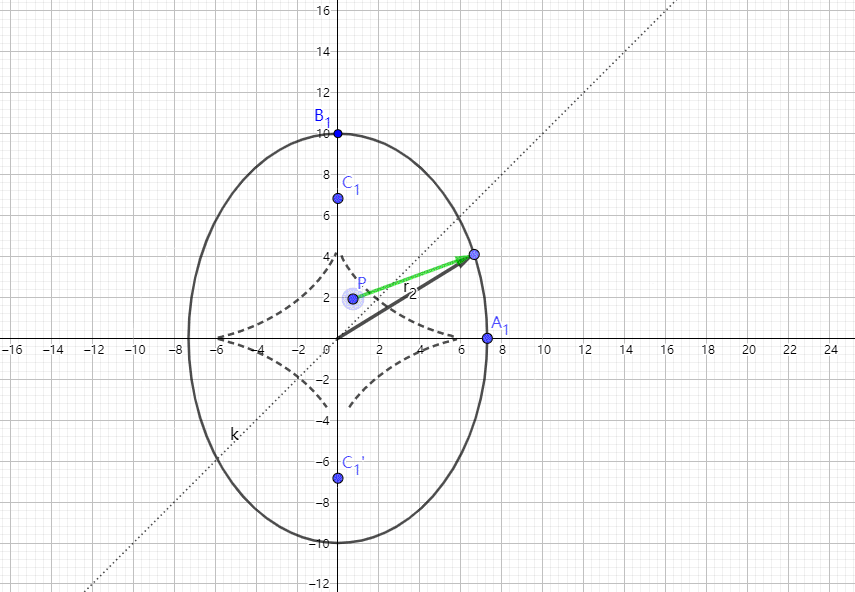
另外,对于2D的准确的椭圆的SDF计算方法,我也根据代码里面的公式绘制了一下动图,希望可以给有兴趣的读者带来一些帮助。里面的虚线代表的是:代码中的d这个变量等于0时p点分布在这条线上。若p点在线的上方,d>0。否则相反。
总结
其实读者也都看出来了,这两篇博客介绍的确实都是一些基础的2D图形的SDF,通常是由直线段以及圆弧构成的。当你确实摸清楚了它们的套路,就会发现其实也并不难。但是对于诸如椭圆、抛物线这样的图形的SDF,以后有机会我可能会继续回来填这个坑,包括3D基本图形的SDF。(谁知道呢)最后再次贴上iq大神文章的地址:https://www.iquilezles.org/www/articles/distfunctions2d/distfunctions2d.htm 。原文的最后介绍了我们最开始提到的这些图形的SDF最终结果减去一个系数能得到带圆角的图形,或者是先取绝对值再减去一个系数能得到一个框,这些也就不在此赘述了,大家应该也很容易理解的。那就先到这里,谢谢阅读~~


