网络流(4)——带有容量的顶点和二部匹配

缓解拥堵的高速公路

　　又是一个晴朗的假日，居住在A城市的上班族打算到附近的B城市看看自然风光。当大家将车开到高速上时，又一次遇到了毫无悬念的拥堵，两个城市间的收费站成了拥堵的重灾区。下图展示了两个城市间高速公路的网络模型。

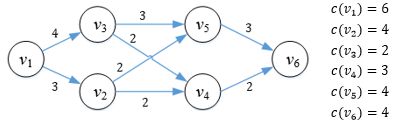
　　图1

　　每个顶点代表一个收费站，v1是A城市的出口，v6是B城市的入口，边的权重代表高速公路的运力c(v1)~c(v6) 代表每个收费站的容量，该容量和高速公路的运力单位相同。为了缓解拥堵，两个城市向每个收费站加派了交警，以便引导司机走相对快速的路线。交警该以怎样的方案调度车辆呢？

带有容量的顶点

　　交通流正好可以规约成网络流模型，但由于加入了顶点的容量，问题似乎也变得更加复杂。回顾流网络的定义，G=(V,E,s,t,C)并没有包括顶点的容量，想要将图1规约成网络流模型，需要先想办法去掉顶点的容量。

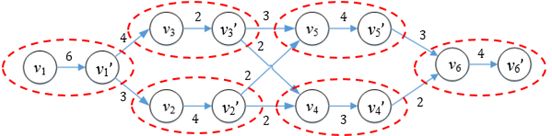
　　我们的解决方案是用边代替顶点，具体做法是对每个有容量顶点v，都添加一个新的顶点v’，连接vv’，使c(v→v’)=c(v)，并将v的流出边转移到v’上：

　　图2

交警的指挥方案

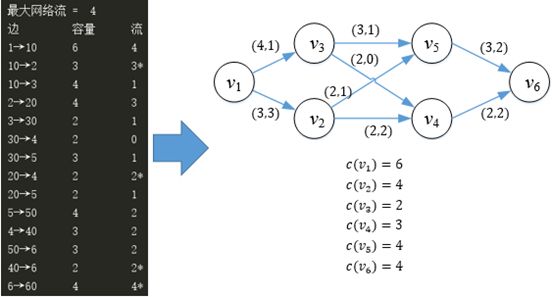
　　图2已经将带有容量的顶点转换成了一个普通的st-网，只要更改一下输入，就可以使用最大流的相关算法找出车辆调度方案。程序中将顶点v的值乘以10作为v’。

 1 import network_flow as nf
 2
 3 V = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
 4 E = [nf.Edge(0, 1, 18), nf.Edge(0, 2, 18), nf.Edge(0, 3, 18), nf.Edge(1, 4, 9), nf.Edge(1, 5, 9),
 5      nf.Edge(2, 5, 9), nf.Edge(2, 6, 9), nf.Edge(3, 6, 9), nf.Edge(3, 7, 9), nf.Edge(4, 8, 3),
 6      nf.Edge(4, 9, 12), nf.Edge(5, 9, 6), nf.Edge(5, 10, 14), nf.Edge(6, 10, 7), nf.Edge(6, 11, 5),
 7      nf.Edge(7, 11, 10), nf.Edge(7, 12, 12), nf.Edge(8, 13, 8), nf.Edge(9, 13, 8), nf.Edge(10, 13, 8),
 8      nf.Edge(11, 13, 8), nf.Edge(12, 13, 8)]
 9 s, t = 0, 13
10 G = nf.Network(V, E, s, t)
11 ford_fullkerson = nf.FordFulkerson(G)
12 ford_fullkerson.start()
13 ford_fullkerson.display()

　　可以看到，最大流除了受边的容量影响外，还受到节点容量的影响。

匹配飞行员

　　第二次世界大战期间，英国皇家空军从沦陷国征募了大量外籍飞行员。在执行飞行任务时，由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的两名飞行员，其中一名是英国飞行员，另一名是外籍飞行员，每一名英国飞行员都可以与若干名外籍飞行员很好地配合。在一次大规模战略任务中，如何匹配飞行员才能使皇家空军一次能派出最多的飞机？

不加思索的答案

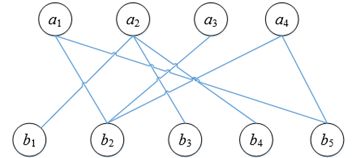
　　假设有m个英国飞行员和n个外籍飞行员，一个不加思索的答案是可以派出min(m, n)架飞机。事实并非如此，可以用图3轻易地反驳。

　　图3

　　a1~a4和b1~b5表示有4名英国飞行员和5名外籍飞行员，其中能够匹配a1、a3、a4的只有b2和b5，因此无法派出4架飞机。

二部匹配

　　图3的模型称为二部图，也叫二分图。二部图的顶点分属于两个集合A和B，对于图中的每无向条边vw来说，都有v属于A且w属于B。基于二部图模型的匹配方案称为二部匹配。

　　一种找到匹配的方案是使用穷举搜索，但是这种方案太过低效，找出最佳匹配可能要搜索所有的匹配方案。假设A集合中有m个顶点，每个顶点都能够发出k条边，那么穷举法在极端情况下需要执行km次才能得出结果，这种指数爆炸级的效率显然是不可接受的。

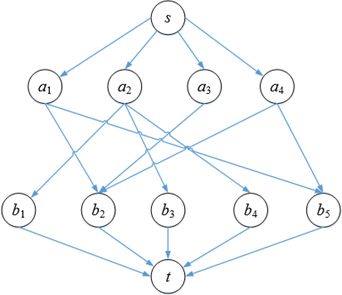
　　网络流可以有效地处理二部匹配，再此基础上加上超级源点和超级汇点，并令每条边的容量为1，这就把一个二部图变成了一个流网络：

　　由于每条边的容量都是1，因此网络流总是能够提供一个合法的匹配，使每个内部顶点至多只有一个单位的流，这相当于A中的顶点至多只能和B中的一个顶点相匹配。现在可以很容易地找到飞行员的匹配方案了。

 1 import network_flow as nf
 2
 3 V_EN = ['a1', 'a2', 'a3', 'a4']
 4 V_FN = ['b1', 'b2', 'b3', 'b4', 'b5']
 5 s, t = 's', 't'
 6 V = [s] + V_EN + V_FN +  [t]
 7 E = [nf.Edge(s, pilot, 1) for pilot in V_EN] + [nf.Edge(pilot,t, 1) for pilot in V_FN]
 8 E += [nf.Edge('a1', 'b2', 1), nf.Edge('a1', 'b5', 1), nf.Edge('a2', 'b1', 1), nf.Edge('a2', 'b3', 1),
 9       nf.Edge('a2', 'b5', 1), nf.Edge('a3', 'b2', 1), nf.Edge('a4', 'b2', 1), nf.Edge('a4', 'b5', 1)]
10
11 class FordFulkerson_Pilot(nf.FordFulkerson):
12     def display(self):
13         print('最大网络流 = ', self.max_flow)
14         print('%-10s%-8s%-8s' % ('边', '容量', '流'))
15         for e in self.G.E:
16             if e.flow == 1:
17                 print('%-10s%-10d%-8s' % (e, e.cap, str(e.flow) + '*'))
18
19 G = nf.Network(V, E, s, t)
20 ford_fullkerson = FordFulkerson_Pilot(G)
21 ford_fullkerson.start()
22 ford_fullkerson.display()

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”