哈希表与区块链的简单介绍
什么是哈希?
简单来说,哈希就是输入任意长度的字符串都可以产生固定大小的输出。在比特币这种加密货币中,交易就是输入,然后经过哈希算法(比特币采用的是 SHA - 256),产生固定长度的输出。
下面就是使用 SHA-256 算法的例子:
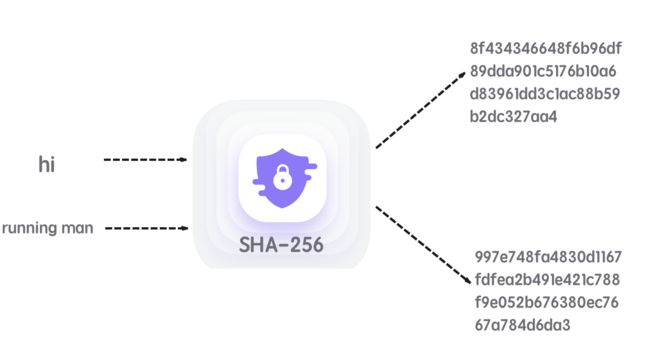 通过上面的例子可以看出,无论输入大或者小,输出都是固定256比特的长度。这一特性在处理大量数据和交易时是至关重要的。基于哈希这一特性,我们不用记输入数据是多么大,只需要记住hash值即可。在我们进一步讨论之前,我们首先需要看看哈希函数的各种属性以及它们在区块链中的实现方式。
通过上面的例子可以看出,无论输入大或者小,输出都是固定256比特的长度。这一特性在处理大量数据和交易时是至关重要的。基于哈希这一特性,我们不用记输入数据是多么大,只需要记住hash值即可。在我们进一步讨论之前,我们首先需要看看哈希函数的各种属性以及它们在区块链中的实现方式。
加密哈希函数
加密哈希函数是一类特殊的哈希函数。为了让哈希函数达到密码安全,需要有以下几个特性:
确定性(Deterministic)
对于同一个输入,无论用哈希函数计算多少次,都会得到相同的结果。
快速计算
对于输入的字符串,能在合理的时间内算出哈希函数的输出,否则会影响系统的性能。
隐秘性
如果我们已知字符串 A 的哈希值是 H(A),那么我们没有可行的办法算出 A 是什么。注意,这里说的是 “不可行” 而不是 “不可能”。 比如下面的例子中,知道输出哈希值是可以算出输入的。
假如我们掷骰子,输出就是骰子上数字的哈希值。那么在知道输出的哈希值情况下,我们能否知道骰子上的数字呢?因为哈希函数是具有确定性的,相同输入的哈希值一定相同,所以我们只需计算 1-6 的哈希值是什么,然后对比就能知道骰子上的数字是什么了。
当然,我们能够根据哈希值猜出骰子的数字,是因为输入值只有 6 种可能性。如果我们的输入值来自一个分散的集合,那么想要通过输出推导出输入的唯一方法可能就是“暴力破解法”了。暴力破解就是,任意选择一个输入,计算其哈希值,与现有哈希值对比是否一致,不断重复这一过程,直到找到一个输入的哈希值与现有哈希值一致。
那么暴力破解法是否可行呢?假设我们现在处理的是128位的哈希值。
最好的情况:第一次尝试就找到了答案,但这种情况可以说是几乎不可能的,比中大乐透还难。
最坏的情况:在尝试 2^128 -1 次后得到了答案,也就是试过了所有可能的输入才找到。
平均的情况: 在平均情况下,我们要尝试 2^128 / 2 = 2^127 次之后才能找到答案。2^127 = 1.7 X 10^38 , 也可以说是个天文数字了。
所以,在已知哈希值的情况下, 尽管可以通过暴力破解的方法找到输入的字符串是什么,但这会花费很长长长长长的时间,所以不用担心。
抗篡改能力
对于任意一个输入,哪怕是很小的改动,其哈希改变也会非常大。比如 “This is a test” 对应的哈希值是C7BE1ED902FB8DD4D48897C6452F5D7E509FBCDBE2808B16BCF4EDCE4C07D14E, 而 “this is a test” 对应的哈希值是 2E99758548972A8E8822AD47FA1017FF72F06F3FF6A016851F45C398732BC50C。
看上面的例子,即便只改变了输入字符串第一个字母的大小写,输出hash值也是完全不同的。用前段时间比较流行的区块链撸猫游戏类比一下,“This is a test” 的哈希值对应猫可能是这样的:
而只改了个大小写,“this is a test” 的哈希值对应猫可能就变成下面这样了: 喵喵~
喵喵~
这一特性对于区块链来说十分重要,因为它决定了区块链是 immutable 的(不变的)。
抗碰撞能力
碰撞是指,对于相同的输入,经过哈希计算后产生了不同的输出。具有抗碰撞能力就是对于大部分的输入都有独一无二的输入。 这里说的是”大部分”,因为找不到碰撞,并不意味不存在碰撞。概率学中的生日悖论可以证明这一点。
生日悖论: 指如果一个房间里有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。
没有哪个哈希函数是完全具有防碰撞特性,但对于 SHA -256 之类的哈希函数,需要花费很长的时间来找到碰撞。所以我们完全可以认为 if H(A) = H(B) 那么 A=B.
谜题友好
这一特性对加密货币来说至关重要(特别是在挖矿过程中)。先定义下什么是谜题友好。
谜题友好: 如果对于任意 n 位输出值 y, 假定 k 选自高阶最小熵分布,如果无法找到一个可行的办法,在比 2^n 小很多的时间内找到 x , 保证 H(k|x) = y 成立,那么我们称哈希函数 H 具有谜题友好的特性。
什么是高阶最小熵?
高阶最小熵描述了分布的分散程度。在这样的分布中,任意数值被选定的概率的小到可以忽略不计的。举个例子,如果要从 1-5 中选择一个数,就是低阶最小熵的分布。如果从 1-无穷大中选择一个数,就是高阶最小熵的分布。
’k|x’代表了什么?
‘|’ 是连接符的意思,将两个字符串连接起来。举个例子’cute|giraffe’ = ‘cutegiraffe’。
再来回顾下谜题友好的定义。假设有一个 n 位输出值 y, 从高阶分布中选取一个任意值 k, 那么没有一个可行的办法,比 2^n 小很多的时间内找到 x ,使得 H(k| x) = y。
这里说的还是 “不可行”,而不是 “不可能”。整个的比特币采矿的过程就基于解谜。
下面是几个典型的加密哈希函数:
- MD5:产生 128 位哈希。
- SHA-1:产生 160 位哈希。
- SHA-256:产生 256 位哈希。也是比特币中使用的哈希函数。
- Keccak-256:产生 256 位哈希,在 Ethereum 中使用。
哈希与数据结构
如果想要理解区块链是怎样工作的,就必须要理解其中 3 种重要的数据结构 哈希指针 , 区块链 和 梅克尔树。
哈希指针
与不同指针不同的是,哈希指针的值是通过数据计算出来的且指向数据所在位置,所以哈希指针可以告诉我们数据存储位置及数据的哈希值。通过哈希指针,我们可以很容易判断出数据是否有被篡改。
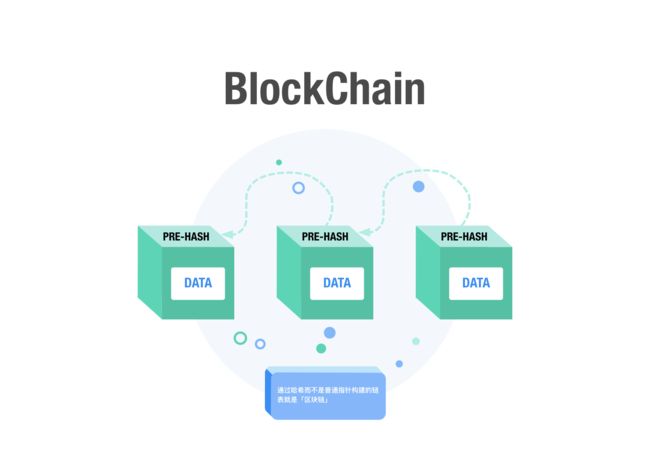
哈希指针在区块链中极为重要。区块链的结构就是由创世区块开始,之后的每个区块通过哈希指针进行连接。每一个区块中都包含了前一个区块的哈希指针,这样后面区块不仅可以查找到前面所有区块,也可以验证前面区块数据有没有被更改,从而保证了区块链不易篡改的特性。
哈希指针在区块链中第二个用处就是构建Merkle Tree(梅克尔树),下文会详细讲。
区块链
区块链是一个基于哈希指针构建的一个有序的,反向链接的交易块链表,也就是说在区块链中每个区块都通过哈希指针连接到前一个区块上。大致结构如下图:
区块链也常被看做一个垂直的堆栈,区块在栈顶一次追加,第一个区块也就是整个堆栈的基础。所以也常常用“高度”(height) 这个词来描述某个区块到第一个区块的距离。
区块链中的每一个区块都有一个对区块头部进行 SHA256 加密哈希函数计算得出的哈希值作为标识。由于每个区块需要连接到前一个区块,所以每个区块头部专门有一个字段用来存储前一个区块(也叫父区块)的哈希值。这样每个区块都连接到了他们的父区块,从而创建了区块链。
尽管每一个区块只能由一个父区块,但却可能短时间内拥有多个子区块。也就是说可能存在多个区块头部中存储的父区块的哈希值是一样的。这种情况一般发生在不同的区块在同一时间被不同的矿工找到。这样就会造成区块链的分叉,如下图: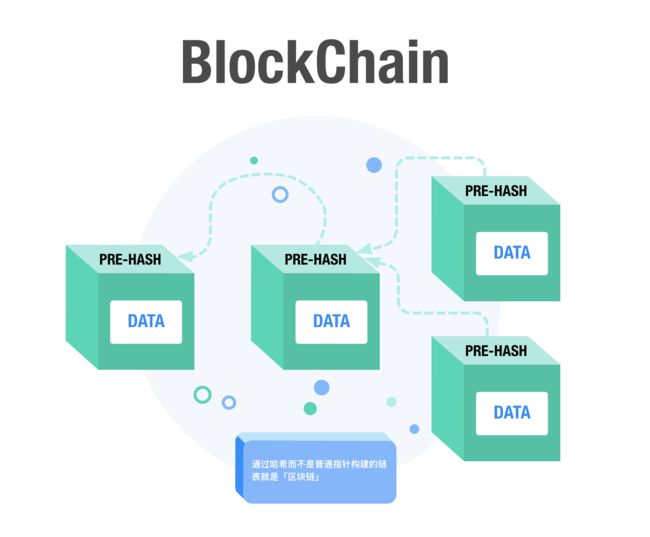 区块链分叉
区块链分叉
不过区块链的分叉只是暂时,会根据“最长链原则”来解决分叉。不是本文重点不再赘述。
刚刚第二节提到哈希指针可以保证区块链不易被篡改,下面来分析下原因。
假设有一个黑客想要篡改上图中 区块 2 的数据。由于哈希函数具有抗篡改能力,很小的改动,输出的哈希值会大不一样。所以如果改动区块2上的数据,那么 区块3 自身的哈希会发生变化。 而 区块3 的头部中存储了 区块2 的哈希值,所以 对区块2 的改动必然会影响到 区块3,以此类推,区块3后面的区块也会受到影响。所以一个区块的修改会级联影响到它之后的所有区块,而要修改之后的所有区块需要强大的算力,可以说是不可能的,这也就保证了区块链的不变性。
仔细看下区块链中每个区块的结构。
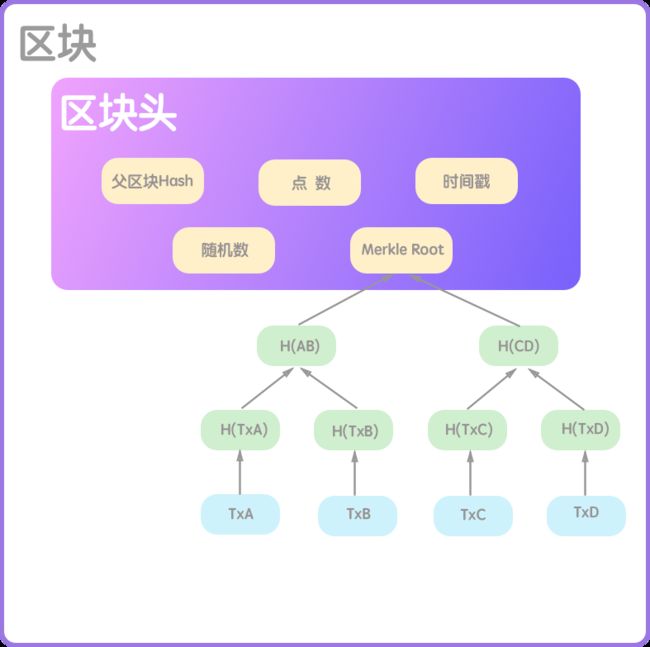
区块的结构
区块的内部结构分为 头部, 元数据,和一系列的交易记录。头部大小是 80个字节,而一个交易记录至少要50个字节,平均每个区块包含超过500个交易记录。所以,一个完整的区块的大小一般是它头部大小的1000倍。 下图是一个区块的大致结构。
区块的头部
如上图,区块的头部的组成分为3大块。第一块是前面区块的哈希值,用于连接到父区块。第二块包含了一个随机数,一个点数(用来表示找到这个区块的难度),和一个时间戳,这三个字段都与挖矿的过程息息相关。第三块是梅克尔树(merkle tree )的树根,merkle tree 用来将区块内的所有交易以一种非常高效的形式组织起来。
merkle tree 相关内容下文会有涉及,随机数、点数和时间戳都是与挖矿相关的。
区块的标识:区块头部哈希值和区块高度
一个区块最主要的标识就是区块自身头部进行二次哈希计算产生的加密哈希值。区块链中第一个区块的哈希值就是 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f 。
区块的另一个标识是它在区块链当中的位置。需要注意的是一个区块只能有一个高度,但在区块链存在分叉的情况下,可能存在多个区块具有一样的高度。这时,区块的高度就不能作为唯一标识了。
第一个区块 : 创世区块
区块链中的第一个区块是2009年创建的,叫做“创世区块”。它是区块链中所有区块的祖先,从任何一个区块向前追溯,最终都会到达创世区块。
通过 blockchain.info 之类的网站查看创世区块的内容 https://blockchain.info/block/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
{
"hash" : "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
"confirmations" : 308321,
"size" : 285,
"height" : 0,
"version" : 1,
"merkleroot" : "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
"tx" : [
"4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b"
],
"time" : 1231006505,
"nonce" : 2083236893,
"bits" : "1d00ffff",
"difficulty" : 1.00000000,
"nextblockhash" : "00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048"
}比特币的创始人中本聪还在创世区块里留下一句永不可修改的话“The Times 03/Jan/2009 Chancellor on brink of second bailout for banks” (2009年1月3日,财政大臣正处于实施第二轮银行紧急援助的边缘), 这句话是泰晤士报当天的头版文章标题。
连接区块到区块链
比特币中每一个节点都存储了从创世区块开始的区块链的本地副本,本地区块链的副本会在新的区块被发现并且添加到区块链后更新。当一个节点从网络接收到一个区块时,会验证该区块,验证通过后将其添加到已有区块链上。
为了建立连接,每个节点都会检验接收到的区块的头部,找到头部中存储的父区块的哈希值。举个例子,一个节点的区块链中有 277314 个区块,最后一个区块头部的哈希值计算出是00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249。
这时节点接收到一个新的区块,内容如下:
{
"size" : 43560,
"version" : 2,
"previousblockhash" :
"00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249",
"merkleroot" :
"5e049f4030e0ab2debb92378f53c0a6e09548aea083f3ab25e1d94ea1155e29d",
"time" : 1388185038,
"difficulty" : 1180923195.25802612,
"nonce" : 4215469401,
"tx" : [
"257e7497fb8bc68421eb2c7b699dbab234831600e7352f0d9e6522c7cf3f6c77",
#[... many more transactions omitted ...]
"05cfd38f6ae6aa83674cc99e4d75a1458c165b7ab84725eda41d018a09176634"
]
}
在验证完成之后,节点会先找到新区块头部中存储的 父区块 的哈希值,比较与最后一个区块的哈希值是否一致。是一致的就把新区块连接到区块链上,这时区块链的高度就变为了277315。
什么是梅克尔树?
在区块的头部中,有存储一个梅克尔树根的 hash 值。所以先来了解下什么是梅克尔树。
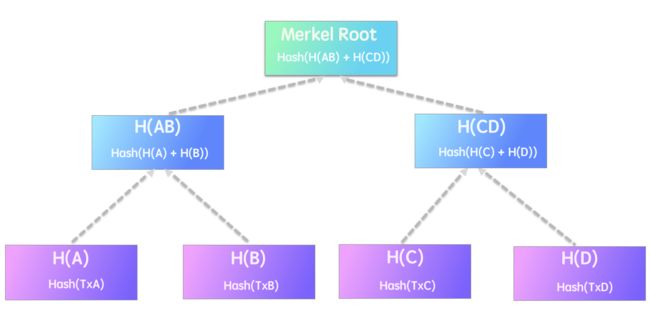
上图就是梅克尔树的样子。
梅克尔树在区块链中用于组织和记录存储在区块中的交易,以便高效的验证某个交易是否存在在区块中。梅克尔树是通过不断的递归计算节点的哈希值直到只有一个hash值来构建的。
当梅克尔树中有N个数据时,最多只需要2*log2(N)计算就可以验证某个特定数据是否存在,所以梅克尔树是相当高效的。
梅克尔树是自底向上构建的。举个例子,假设我们现在有 A, B, C,D四笔交易需要存储记录在区块中,来看下是如何构建梅克尔树的。 首先要用 A,B,C,D 来构建树的叶子节点,将他们二次哈希后的哈希值存储在是叶子节点,就是上图中的 HA,HB,HC,HD。
H(A) = SHA256(SHA256(A))接着再用相邻两个结点的hash值连接在一起经过二次哈希计算来构建它们的父节点
H(AB) = SHA256(SHA256(H(A) + H(B)))这一过程一直重复到只剩下顶层的一个节点,也就是存储在区块头部的树的根节点。
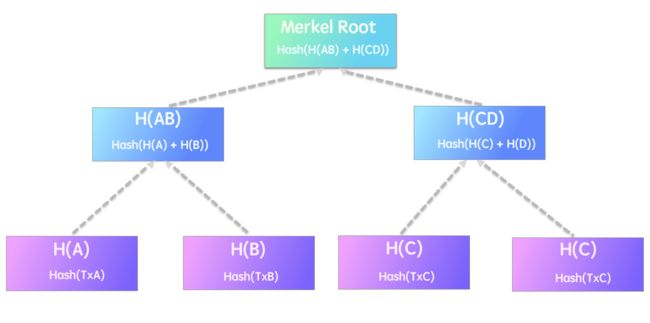
因为梅克尔树是一棵二叉树,它需要偶数个叶子节点。如果恰好是奇数个交易,那么最后一笔交易会被复制一遍,来创造偶数个叶子节点,以便达到平衡。下图中的交易 C 就被复制了一遍。
根据上面的方式我们可以为任意个数的交易构建梅克尔树,一个区块通常要记录几百到上千的交易。
为了验证一笔交易是否包含在区块中,节点只需要 计算 log2(N) 个哈希值,组成该交易到merkle树根的认证路径即可。正因为梅克尔树,区块链中的节点可以快速的产生一条包含10或12个哈希值的认证路径,来证明在区块中上千笔交易中某笔交易的存在。
哈希与挖矿
我们说的“挖矿”,就是指找到可以加入区块链的新的区块。矿工们要不断的工作在确保区块链的增长的同时获到新区块的奖励。早些时候,人们往往使用笔记本电脑挖矿,但随着时间的推移,大家开始组成矿池以便集中算力更高效的挖矿。
这里存在一个问题,每种加密货币都有一个上限,比如,比特币一共有2100万个。如果找到新区块的速度过快,那么很快所有的比特币就被挖完了。所以,需要控制找到新区块的速度。对于比特币,新区块创建的时间间隔被控制在10分钟左右。
为了控制区块的创建速度,设置了一个目标值。一个有效区块的头部哈希值必须要小于目标值。目标值是一个以一串0开头的64位的字符串,开头的0越多难度越大,每新产生2016个区块之后目标值会调整一次。区块的头部有个随机数的字段,其实挖矿的过程也就是找到一个可以使区块头部哈希值小于目标值的随机数的过程,也叫做解迷。
总结
哈希在区块链技术中是最基础的。如果想要了解区块链是什么,就必须要了解什么是哈希,它有什么特性,在区块链中起着什么作用。