HNUCM2020年春季ACM集训队热身赛-第1场题解

问题 A: 狮子座的失眠

题目描述

狮子座自从上次几乎素数问题没有解决后，开始了失眠之夜，于是他开始了念数字游戏，不过他念的方式很奇妙，他念的是每个数字的拼音，例如：-600 他念的是“fu liu ling ling”。

输入

输入一个整数，保证最多只有4位数，输出每个数字对应的拼音。当整数为负数时，先输出fu字。

输出

在一行中输出这个整数对应的拼音，每个数字的拼音之间用空格分开，行末没有最后的空格。如 yi er san si。

样例输入

-600

样例输出

fu liu ling ling

思路

用数组存0-9每一个数字对应的拼音
将输入的数字用while循环拆分每一位的数字存到数组中（这样得到是逆序的），逆序输出每一位对应的拼音（逆逆得正…）

#include
using namespace std;
char s[10][6]={"ling","yi","er","san","si","wu","liu","qi","ba","jiu"};
int w[5],lw;
int main()
{
    int n;
    while(~scanf("%d",&n)){
        if(n<0){
            printf("fu ");
            n=-n;
        }
        lw=0;
        while(n){
            w[++lw]=n%10;
            n/=10;
        }
        for(int i=lw;i>=1;--i){
            printf("%s%c",s[w[i]],i==1?'\n':' ');//三目运算符
        }
    }
    return 0;
}

---

问题 B: 狮子座的简单统计题

题目描述

编写程序统计每种不同的个位数字出现的次数。例如：给定 N=100311，则有 2 个 0，3 个 1，和 1 个 3。

输入

每个输入包含 1 个测试用例，即一个不超过 1000 位的正整数 N。

输出

对 N 中每一种不同的个位数字，以 D:M 的格式在一行中输出该位数字 D 及其在 N 中出现的次数 M。要求按 D 的升序输出。

样例输入

100311

样例输出

0:2
1:3
3:1

思路

用数组统计每个数字出现次数，最后遍历一遍将非0的输出

#include
using namespace std;
const int maxn=2e5+5;
int num[15];
char s[maxn];
int main()
{
    while(~scanf("%s",s+1)){
        int ls=strlen(s+1);
        for(int i=1;i<=ls;++i){
            ++num[s[i]-'0'];
        }
        for(int i=0;i<=9;++i){
            if(num[i]){
                printf("%d:%d\n",i,num[i]);
            }
        }
    }
    return 0;
}

---

问题 C: 狮子座的复杂统计题

题目描述

狮子座很快就把简单统计题ac了，现在他遇到了一个复杂的统计题。
有一组数据，你需要编程来求出次数出现最多的数字，保证输入是从小到大排序好了的。
如果有两个元素值出现的次数相同，即并列第一，那么只打印比较小的那个值。

输入

第一行输入一个整数 N ，N<=20 ，接下来有N个数字，保证从小到大排序，保证都在 int 范围内。

输出

输出只有一行，即出现次数最多的那个元素值。如果次数相同，输出较小的那个值。

样例输入

5
100
150
150
200
250

样例输出

150

思路

输入是排好序的，相同的数字肯定相邻，正序遍历维护每个数字出现的次数

#include
using namespace std;
const int maxn=2e5+5;
const int inf=0x3f3f3f3f;
int w[maxn];
int main()
{
    int n,x;
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i){
            scanf("%d",&w[i]);
        }
        int num=-inf,ma,now=1;
        for(int i=2;i<=n;++i){
            if(w[i]==w[i-1]){
                ++now;
            }else{
                if(now>num){
                    ma=w[i-1];
                    num=now;
                }
                now=1;
            }
        }
        printf("%d\n",ma);
    }
    return 0;
}

---

问题 D: 狮子座的水题

题目描述

狮子座最近在OJ做了一道最小公倍数的题，ac之后特别有成就感，还发现了gcd函数，于是他觉得最小公倍数问题都是水题了。突然，一个叫“欧几里得”的dalao重新排了一道关于最小公倍数的题，题目如下：求出n个数的最小公倍数。 于是，狮子座顿时方了，他只会求两个数的最小公倍数。此时向你求助，请帮助他完成这道题。

输入

输入包含多个测试实例，每个测试实例的开始是一个正整数n，然后是n个正整数。保证都处于int范围内。

输出

为每组测试数据输出它们的最小公倍数，每个测试实例的输出占一行。

样例输入

2 4 6

样例输出

12

思路

因为
x×y=(x和y的最大公因数)×(x和y的最小公倍数)
所以
x和y的最小公倍数=x×y/x和y的最大公因数
但这样只能求两个数的最小公倍数
多个数的最小公倍数可以第一个数和第二个数求最小公倍数，得到的数和第三个数求最小公倍数…直到最后一个

#include
#define ll long long
using namespace std;
ll gcd(ll a,ll b){
    return b==0?a:gcd(b,a%b);
}
int main()
{
    int n;
    while(~scanf("%d",&n)){
        ll ans,a;
        scanf("%lld",&ans);
        for(int i=2;i<=n;++i){
            scanf("%lld",&a);
            ll x=gcd(ans,a);
            ans=(ans*a)/x;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

---

问题 E: 幸运数

题目描述

众所周知，不管是人还是熊都需要人品。于是乎，为了给自己找一个幸运数字，Mavis 学习了人类的阿拉伯数字，并不知从哪儿弄来了一串序列和一个 S，Mavis 说：“长度最短且和大于等于 S 的连续子段的长度， 就是俺的幸运数字”！

但是 Mavis 只会喊口号，不会解决问题，所以这个问题就交给你了。

输入

输入文件共三行。

第一行输入仅一个正整数 n，意义如题所述。（ n ≤ 4000000, ai ≤ 10^9)

第二行输入 n 个正整数 ai，表示序列中的元素。

第三行输入仅一个正整数 S，意义如题所述。

每两个输入的数之间都用一个空格隔开。

输出

输出文件仅一行一个整数，表示幸运数。

样例输入

8
4 12 10 18 17 10 17 17
40

样例输出

3

思路

二分法
区间答案满足单调性
可以二分区间，既然题目没有说没有答案的情况，那我们就默认一定有答案，可能的答案长度为1~S的长度，循环判断长度是否可行

#include
#define ll long long
using namespace std;
const int maxn=4e6+5;
ll a[maxn],m;
int n;
bool ju(int mid){
    ll now=0;
    for(int i=1;i<=mid;++i)
        now+=a[i];
    if(now>=m)
        return true;
    for(int i=mid+1;i<=n;++i){
        now=now+a[i]-a[i-mid];
        if(now>=m)
            return true;
    }
    return false;
}
int main()
{
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i){
            scanf("%lld",&a[i]);
        }
        scanf("%lld",&m);
        int l=1,r=n,mid,ans;
        while(l<=r){
            mid=(l+r)>>1;
            if(ju(mid)){
                ans=mid;
                r=mid-1;
            }else{
                l=mid+1;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

---

尺取法
相当于我们有一个虚拟的尺子，尺子的左右端点分别为l和r，当这个区间和小于S时我们将r向右移动，直到大于等于S，取最小值，然后如果区间和足够，将l向右移动一格…
尺取法入门

#include
#define ll long long
using namespace std;
const int maxn=4e6+5;
ll a[maxn];
int main()
{
    int n,m;
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i){
            scanf("%lld",&a[i]);
        }
        scanf("%d",&m);
        int l=1,r=1,ans=n;
        ll now=0;
        while(r<=n){
            while(now<m&&r<=n){
                now+=a[r++];
            }
            if(now<m)
                break;
            ans=min(ans,r-l);
            now-=a[l++];
        }
        printf("%d\n",ans);
    }
    return 0;
}

---

问题 F: 跳跃版图

题目描述

有一个 n×n 的格子，每个格子中有一个非负整数。你的目标是从左上角跳到右下角，每步只能向右或向下跳。格子中的数代表从该格开始跳跃的前进步数，如果某次跳跃会跃出格子 界限则该跳跃是禁止的。注意 0 是一个绝对终点，因为从这里无法再移动。

你的任务是统计有多少种合法路径。上图 1 中共有 3 种路径，分别表示在图 2 中。

输入

第一行，一个整数 n（3 ≤ n ≤ 100）。

接下来 n 行 n 列，表示格子中的数，所有数的范围在[0,9]中，两个数之间用一个空格隔开。

输出

第一行，从左上角到右下角的合法路径数目。

样例输入

4
2 3 3 1
1 2 1 3
1 2 3 1
3 1 1 0

样例输出

3

思路

动态规划+大数
step[i][j]表示从左上角走到点（i，j）的路径数，转移的时候判断是否出界
状态转移方程

step[i][x+j]=step[i][x+j]+step[i][j];
step[x+i][j]=step[x+i][j]+step[i][j];

因为n的极限范围是100，当版图中所有的数都是1的极限状况时，肯定会超出整形和长整型的存储范围
所以还要用大数加法
大数入门

#include
#define ll long long
using namespace std;
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
struct node{
    int s[205],ls;
    void cl(){
        memset(s,0,sizeof(s));
        ls=1;
    }
    node operator+(const node &a)const{
        node ans;
        ans.cl(),ans.ls=max(ls,a.ls);
        for(int i=1;i<=ans.ls;++i){
            ans.s[i]=ans.s[i]+s[i]+a.s[i];
            if(ans.s[i]>9){
                ans.s[i+1]+=ans.s[i]/10;
                ans.s[i]%=10;
            }
        }
        if(ans.s[ans.ls+1]>0){
            ++ans.ls;
        }
        return ans;
    }
};
node step[105][105];
int main()
{
    int n,x;
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                step[i][j].cl();
            }
        }
        step[1][1].s[1]=1;
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                scanf("%d",&x);
                if(x==0)
                    continue;
                if(x+j<=n)//向右
                    step[i][x+j]=step[i][x+j]+step[i][j];
                if(x+i<=n)//向下
                    step[x+i][j]=step[x+i][j]+step[i][j];
            }
        }
        for(int i=step[n][n].ls;i>=1;--i){
            printf("%d",step[n][n].s[i]);
        }
        putchar('\n');
    }
    return 0;
}

---

问题 G: 耶路撒冷战役

题目描述

第二次十字军东征末期，由阿拉伯领袖萨拉丁率领的阿拉伯联军兵临圣城耶路撒冷。在城内驻扎的圣殿骑士团被歼灭之后，阿拉伯大军兵临城下。

来到山岗上，萨拉丁极目远眺，见两小儿辩日， 发现自己的军队排成了一个 NM 大小的方阵。作为一个的军事家，这种阵型是他非常抵触的。于是他打算将他的军队分割成1*1大小的小队。

然而拆分整编的军队是很费时间的一件事，对于行与行之间的每一条横线，列与列之间的每一条竖线，都有一个耗费时间的值（可以相同）。更加麻烦的是，拆分后的军队都是独立的，两个独立的部分不能拼接在一起拆分（比如一个显示器被拆成了两半，想把它拆成四份则需要对于已有的两份分别再拆一次） 。

现在萨拉丁知道每一条横线和每一条竖线耗费时间的值，但是他很忙，所以不能处理出将NM的方阵拆成1*1的小队的总消耗时间的最小值，于是他转向你帮忙。

输入

第一行包含两个数N与M，分别表示行和列的数量。

接下来N-1行，表示每一条横线的耗费时间值。

接下来M-1行，表示每一条竖线的耗费时间值。
1 <= N , M <= 2000

输出

一个数表示总耗费时间的最小值。

样例输入

2 2
3
3

样例输出

9

思路

贪心思想
如果两条线同为行或者同为列，它俩拆的顺序是没有影响的，比如a和b同为行，那么先拆a后拆b和先拆b后拆a耗费的时间相等。
但行列之间是会互相影响，每拆一个行，后续列拆除的时候要多拆一次，也就是多消耗一次的时间。
比如有三行（2，2，2）一列（5）
如果直接拆列，拆列的时候需要耗费5
如果先拆一个行，再拆列，拆列的时候需要耗费10
如果先拆两个行，再拆列，拆列的时候需要耗费15
…
列同理
也就是每拆一个行后续的列拆除的时候都要多拆一次。每拆一个列后续的行拆除的时候都要多拆一次
所以要将耗费时间多的先拆
…
将行列分别排序
每次取行列中的最大值，如果是行那耗费的时间即为前面拆除的列的数量+1，如果是列那耗费的时间即为前面拆除的行的数量+1

#include
#define ll long long
using namespace std;
const int maxn=1e5+5;
int a[maxn],b[maxn];
bool cmp(int a,int b){
    return a>b;
}
int main()
{
    int n,m;
    while(~scanf("%d %d",&n,&m)){
        for(int i=1;i<n;++i)
            scanf("%d",&a[i]);
        for(int i=1;i<m;++i)
            scanf("%d",&b[i]);
        sort(a+1,a+n,cmp);
        sort(b+1,b+m,cmp);
        int x=1,y=1;
        ll num_x=1,num_y=1,ans=0;
        while(x<n&&y<m){
            if(a[x]>b[y]){
                ans+=num_y*a[x];
                ++num_x,++x;
            }else{
                ans+=num_x*b[y];
                ++num_y,++y;
            }
        }
        while(x<n){
            ans+=num_y*a[x];
            ++num_x,++x;
        }
        while(y<m){
            ans+=num_x*b[y];
            ++num_y,++y;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

---

问题 H: Fy’s dota2

题目描述

Fy 觉得自己玩 cf，lol这种高端游戏已经够厉害了，于是他决定去玩dota2。结果 fy 的鼠标右键坏了，所以他就等到 2500 买了把闪烁匕首，用跳刀前进，准备去送泉水。但是 fy 一次最多前进 k 的距离，泉水离 fy 现在的距离是 n。

Fy 想知道他到泉水的方案数。

输入

第一行 2 个整数：k，n
1<=n<=2^31-1,1<=k<=10

输出

一行 1 个整数：代表答案对 7777777 取膜的结果

样例输入

2 4

样例输出

5

思路

很容易找出递推式

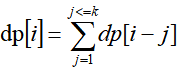
但n的范围太大了，暴力递推肯定会超时
而递推式的优化可以用矩阵快速幂
而且k的范围比较小(暗示矩阵快速幂)
矩阵快速幂入门

构建矩阵

如果k<=n那答案就是2^(n-1)次方，如果k>n那就构造矩阵，计算指数为n-k的矩阵快速幂

#include
#define ll long long
using namespace std;
const int mod=7777777;
int k,n;
struct node{
    ll a[12][12];
    node(){
        memset(a,0,sizeof(a));
    }
    node operator*(const node x)const{
        node ans;
        for(int i=1;i<=k;++i){
            for(int j=1;j<=k;++j){
                for(int p=1;p<=k;++p){
                    ans.a[i][j]+=a[i][p]*x.a[p][j];
                    ans.a[i][j]%=mod;
                }
            }
        }
        return ans;
    }
};
ll pow_(int b){
    node st,mul;
    for(int i=1;i<=k;++i){
        st.a[1][i]=pow(2,k-i);
        mul.a[i][1]=1;
        mul.a[i][i+1]=1;
    }
    while(b){
        if(b&1){
            st=st*mul;
        }
        mul=mul*mul;
        b>>=1;
    }
    return st.a[1][1];
}
int main()
{
    while(~scanf("%d %d",&k,&n)){
        if(k>=n){
            printf("%d\n",(int)pow(2,n-1));
            continue;
        }
        printf("%lld\n",pow_(n-k));
    }
    return 0;
}