Codeforces Round #654 (Div. 2) A-E1 --我的题解

A:

给定从1~n的长度的棒子，要求两两拼接，最多能拼多少根长度一样的棒子

一看就知道，第一个和最后一个拼接，第二个和倒数第二个拼…当然n为偶数时刚刚好，为奇数时最后一个棒子要事先拿出来，前面的如上策略拼，长度刚刚好为最后一个棒子

1.	#include <iostream>
2.	#include <stdio.h>
3.	#include<cstring>
4.	#define F(i,a,b) for(int i=a;i<=b;i++)
5.	#define FD(i,b,a) for (int i=b;i>=a;i--)
6.	#define ll long long
7.	using namespace std;
8.	const ll pm = 1e9 + 7;
9.	 
10.	 
11.	int main()
12.	{
13.	 
14.		int T;
15.		cin >> T;
16.		while (T--) {
17.			int n;
18.			cin >> n;
19.			if (n % 2 == 0) {
20.				cout << n / 2 << endl;
21.			}
22.			else {
23.				cout << (n - 1) / 2 + 1 << endl;
24.			}
25.		}
26.	 
27.		return 0;
28.	}
29.	 

B:

给定一个天数n，你要在一个矩形日历上为连续n天涂上颜色，而且在日历上必须是连续的区域(一个方块至少与另一个方块共边)，这个日历的宽度由你自己定，问能画出多少种不同的图案（在日历上通过平移无法重叠算作不同）

乍一看阅读理解很长，而且比赛组织者还发了俩tips，但其实用一些日常知识确实不难理解，毕竟才第二题。
解法在以前遇到过，当要从第一行末尾涂色到第二行开始时，这种图案整体其实仅仅由第一行的状态决定。所以当宽度确定为x时，整体只有x种不同图案。
但是日历上的色块必须连续，所以对于上述换行的涂色方法日历宽度小于天数n
宽度大于等于n时，只有一种图案——一横排（此时换行涂色法会使区域不连续）

1.	#include <iostream>
2.	#include <stdio.h>
3.	#include<cstring>
4.	#define F(i,a,b) for(int i=a;i<=b;i++)
5.	#define FD(i,b,a) for (int i=b;i>=a;i--)
6.	#define ll long long
7.	using namespace std;
8.	const ll pm = 1e9 + 7;
9.	 
10.	ll calc(ll a, ll b) {
11.		return ((1 + b) * b) / 2;
12.	}
13.	 
14.	int main()
15.	{
16.	 
17.		int T;
18.		cin >> T;
19.		while (T--) {
20.			ll a, b; ll ans = 0;
21.			cin >> a >> b;
22.			if (b >= a) {
23.				ans = calc(a, a - 1) + 1;
24.			}
25.			else
26.			ans = calc(a, b);
27.			cout << ans << endl;
28.		}
29.	 
30.		return 0;
31.	}
32.	 

C:

你有2种饼干，各v、c个，有n个好人，m个坏人来吃你的饼干，一个好人会吃一块当前储量多的饼干，（储量一样时吃c饼干），一个坏人会吃一块当前储量少的饼干，（储量一样时吃v饼干），问有没有一种好人坏人的吃饼干顺序使所有人吃到饼干

其实我翻译过来已经暗示了解法了，如果无法满足坏人，那么肯定无解。
（因为他总是要吃少的，把我家都吃光了！）所以不用多想什么好人会让当前多的饼干吃到和少的饼干数量一样，然后坏人来一吃，和坏人直接吃少的饼干效果一样的！所以直接认定先来的都是坏人

1.	ll min(ll a, ll b) {
2.		if (a > b)return b; else return a;
3.	}
4.	int main()
5.	{
6.	 
7.		int T;
8.		cin >> T;
9.		while (T--) {
10.			ll a, b, n, m; int f = 0;//f=1时表示无解
11.			cin >> a >> b >> n >> m;
12.			if (n + m > a + b) {
13.				f = 1;
14.			}
15.			if (!f) {
16.				if (min(a , b) < m) {
17.					f = 1;
18.				}
19.			}
20.			if (!f)cout << "YES" << endl; else cout << "NO" << endl;
21.		}
22.	 
23.		return 0;
24.	}

D:

给你一个n*n一开始全0的矩阵，你要在上面写k个1，使得（maxR-minR）^ 2 +（maxC-minC）^2最小。其中maxR，minR表示按行数1的个数最多的一行和最少的一行，maxC,minC类似含义。输出最小值和此时的矩阵

显然是一个构造题，我们考虑一个5*5的矩阵 前5个肯定可以是这样

使得每行每列1数都为1，那么接下来我们要让每行每列1数为2（这样至少使得max-min<=1）

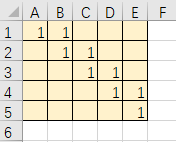
先画4个，显然这样是可行的！那么接下来一个，我们手动数一下，第一列和第5行1数是1，所以下一个：

这里我在矩阵外面多花了一个1，大家一看就懂了，这5个其实和前5个是一样的，只不过对n取模而已
然后类推其实都很清楚了

这样填都是可行的，那么可以类推出只要对角线填法+取模每n个为一组，怎么填都可以
我代码是用的刚刚分析的从正对角线开始填。每一组的初始位置设置比较麻烦但是可以过：

int mp[500][500] = {};
2.	int main()
3.	{
4.	 
5.		int T;
6.		cin >> T;
7.		while (T--) {
8.			int n, m; 
9.			cin >> n >> m;
10.			int px = 0, py = 0; int sx = 0, sy = 0;
11.			memset(mp, 0 ,sizeof(mp));
12.	 
13.			while (1) {
14.				if (!m)break;
15.				F(i, 1, n) {
16.					mp[px % n][py % n] = 1;
17.					px++, py++;
18.					m--;
19.					if (!m) break;
20.				}
21.				if (!m) break;
22.	 
23.				if (sx == 0 && sy == 0) {
24.					sx = 0, sy = 1;
25.					px = 0, py = 1;
26.				}
27.				else {
28.					if (sx == 0) {
29.						sx = sy; sy = 0;
30.						px = sx, py = sy;
31.					}
32.					else {
33.						 sy = sx + 1; sx = 0;
34.						px = sx, py = sy;
35.					}
36.				}
37.				
38.			}
39.			int R[500] = {}, C[500] = {};
40.			F(i, 0, n - 1) {
41.				F(j, 0, n - 1) {
42.					R[i] += mp[i][j];
43.					C[j] += mp[j][i];
44.				}
45.			}
46.			int maxR = 0, minR = 9999, maxC = 0, minC = 9999;
47.			F(i, 0, n - 1) {
48.				if (maxR < R[i]) maxR = R[i];
49.				if (minR > R[i])minR = R[i];
50.				if (maxC < C[i])maxC = C[i];
51.				if (minC > C[i])minC = C[i];
52.			}
53.	 
54.			cout << ((maxR-minR) * (maxR - minR)) + ((maxC-minC) * (maxC - minC)) << endl;
55.			F(i, 0, n-1) {
56.				F(j, 0, n-1) {
57.					printf("%d", mp[i][j]);
58.				}printf("\n");
59.			}
60.	 
61.	 
62.		}
63.	 
64.		return 0;
65.	}

E1:

（比赛时只想到了简单版的解法，所以介绍一下我的简单版做法，后文记录标算）
给你一个长度为n的序列a，你决定一个初始值sta，从序列首位开始一一比较，sta>=a[i] 则sta++，比较下一个，否则退出循环。问能比完整个序列的不同的排序方式有多少，记为ans；
显然这样的ans对于不同的初始值sta是不同的，那么问不能被一个给定质数p（p

首先把这个序列递增排列，这样是最有可能比完整个序列的，简单版a[i]<=2000，所以我直接暴力对sta取值，F(sta,a[1],a[n])
下面对于一个sta，如何得到ans呢。O(1)地算出来我觉得不太科学，所以直接考虑能不能O(n)
简单思考能发现，对于a[i]<=sta的，假设有x个，他们不管怎么排列那么sta在任何情况下都可以比得过他们，这里就有x！种不同排法。
那么对于a[i]>sta的怎么办，他们肯定不能排前面的若干位置，他们最多也就是往前面挪几位，能往前挪的这个位数是看sta的值和i的，如果能往前挪动一位，那么在那些小于等于sta的、进行全排列a[i]的基础上，就多一倍的情况，挪两位就多两倍。
最后ans就等于x！*(每个大于sta的数能往前挪动的数目+1)
因为考虑能不能被p整除 则只要判断p是不是上面这个式子的某一个乘数就行了不用算出ans

注意这里我们只看向前挪形成“相对位置”不同的序列，如果同时又考虑向后挪，那么与后面的一些a[i]向前挪的状态会有重复

#define F(i,a,b) for(int i=a;i<=b;i++)
#define FD(i,b,a) for (int i=b;i>=a;i--)
#define ll long long
using namespace std;
const ll pm = 1e9 + 7;

int queAns[3000] = {};
int a[3000] = {};
void qs(int L, int R) {
	int i = L, j = R;
	int k = a[L + (R - L) / 2];
	while (i < j) {
		while (a[i] < k) i++;
		while (a[j] > k) j--;
		if (i <= j) {
			int t = a[i]; a[i] = a[j]; a[j] = t;
			i++, j--;
		}

	}
	if (L < j)qs(L, j);
	if (i < R) qs(i, R);

}
queue<int>ans;
int main()
{
	int n, p;
	cin >> n >> p;
	F(i, 1, n) {
		scanf("%d", a + i);
	}

	qs(1, n);
	int sta; int ansNum = 0;
	F(i, a[1], a[n]) {
		sta = i; int f = 0;
		F(j, 1, n) {
			if (sta + j - 1 < a[j]) {
				f = 1;
			}
		}
		if (f) continue;
		else {
			int base = 0;
			F(j, 1, n) {
				if (a[j] <= sta)base++;
				else {
					ans.push(sta + (j - 1) - a[j] + 1);
				}
			}

			if (base >= p) f = 1;
			if (!f) {
				while (!ans.empty()) {
					if (p == ans.front()) {
						f = 1;
					}
					ans.pop();
				}
			}
		}
		if (!f) {
			ansNum++;
			queAns[ansNum] = i;
		}
	}
	cout << ansNum << endl;
	F(i, 1, ansNum) {
		cout << queAns[i] << ' ';
	}cout << endl;

	return 0;
}