说明:如果发现错误或者有任何问题,任何不理解的地方请评论提出,或私信me,^ _ ^
ACM—图论 最小环问题(Floyd算法应用)
最小环问题是Floyd算法的应用,并不难,和Floyd算法一样难度。但是如果要输出最小环路径就要稍微麻烦一点,也不难。
1.计算最小环值(HDU 1599)
有向图最小环:
有向图最小环最少要有2个点组成环,这个的写法就是用Floyd()求最短距离,最后所有点中的最短距离的最小值就是答案。
无向图最小环:
肯定和有向环做法有区别,无向图构成环最少要有3个点,所以求最小环可以枚举最大环中的连接点,更新答案。(这里的最大环指的是环中的节点尽可能的多,同时在枚举增加环中点的同时也要使环上边权值最小) ,这里如果不懂可能是我描述问题,实际上不难,请继续看下面的部分会明白的。
(1)和Floyd()关系:
的你肯定好奇这和Floyd()有什么关系?其实仔细想想Folyd()中要遍历所有点作为k点,而我们给最小环中加点是也是遍历所有点去考虑要不要添加这个点,同时我们更新ans时要用到两点间的最短距离dis[i] [j](这个下面会说),所以我们完全可以将更新ans的步骤放在Folyd()的经典的3次循环中。
(2) 如何更新ans:
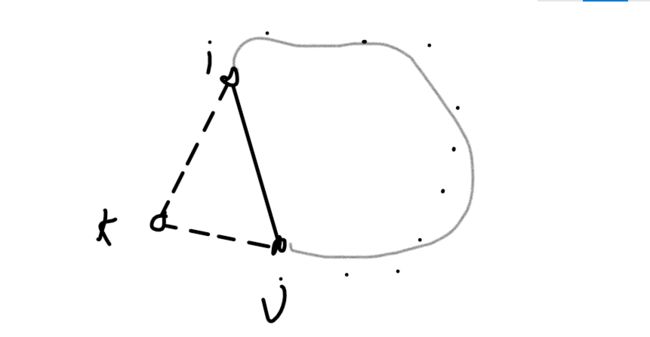
这里直接从开始讲不太容易说明,所以我们先假设已经处理到第k个点了,这意味着1 ~ k-1 的点它们之间的最小值在只有k-1个点的情况下已经确定。这时我们枚举前k-1个点中的两个点 i , j 组合,这里我们可以先认为只有前k-1个点时的最小环已经得出了,就是i , j 与一些点所连的环。
所以很容易想到我们现在的任务是求有前k个点时的最小环值,也就是在前k-1个点中的最小环中添加k,看满不满足加入k点后环上权值和减小,求出这里面的最小值更新ans(未更新前ans是前k-1个点最小环值),由于不保存环,所以每次要枚举前k-1个点中的i,j组合作为插入k的位置。(这里提前说一下:要想将k加入到i,j所在的环里面,k点一定与i,j都相连,注意前面的条件我们就是要从i,j这里加入k,所以一定相连)如何判断环上权值和减少呢?就是ans>dis[i] [j]+e[i] [k]+e[k] [j] (如果k与i,j任意一个不相连这里右边都是INF,不会更新答案)。这也就是前面说要用到dis[] []的原因。
看这幅图,灰色的部分时前k-1个点的最小环,ans就是灰色部分加i,j之间的距离,更新比较的就是灰色部分加k,i边的权值和k,j边的权值。(具体实现见代码讲解)
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MA=1e3+5;
const int INF= 0xfffffff;
int e[MA][MA];//存图
int dis[MA][MA];//两点间的最小距离
int n,m;
int init()//初始化
{
for(int i=1;i<=n;++i){
for(int j=0;j<=n;++j){
if(i==j)e[i][j]=dis[i][j]=0;
else e[i][j]=dis[i][j]=INF;
}
}
}
void Floyd()
{
int ans=INF;//初始化ans
for(int k=1;k<=n;++k){
//注意要先更新ans,再更新dis[][].因为更新ans用的是只有前k-1个点的dis[][]
for(int i=1;ie[a][b])continue;
e[a][b]=e[b][a]=dis[a][b]=dis[b][a]=c;
}
Folyd();
}
return 0;
}
2. 输出最小环路径 ( poj 1734 )
方法1 数组记录前驱:
用一个数组R[i] [j]维护 i 到 j 的最小路径上j上一个点是谁
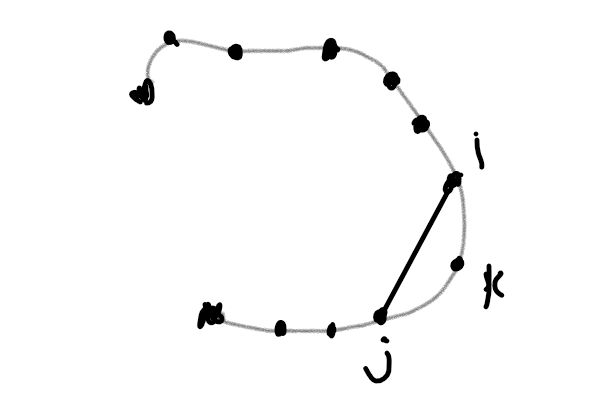
见上图(1) 我们假设从j到i的逆时针的环中的小黑点分别代表这个环里面最小环上的点,分别标为$k_{1},k_{2},k_{3} ···k_{n} $。 (注意离 i 最近的是K~n~ )我们用path[] 记录最小环上的路径。
下面这个图(2)是关于更新最短路的图(3重循环):
步骤:
(1) 初始化R[] [],遍历所有i,j 让R[i] [j]=i,见 图(1) 也就是R[i] [\(k_{n}\)] = R[i] [\(k_{n-1}\)]= · · · R[i][\(k_{1}\)] = R[i] [j] = i 。
(2) 这种做法主要理解R[] []的更新过程,在第二次3重循环松弛最短路过程中(见代码)。首先右边灰色的环就是dis[i] [j] ,(接下来的i,j见图2)而在更新的过程中这条线一旦被哪个 k 点更新,我们就让R[i] [j]=R[k] [j] (也就是R[i] [j]=k)。也就是说最后R[a] [b]保存a,b两点之间最短路径上b前面的点。在图(1)中就是 R[i] [j]=\(k_{1}\), R[i] [\(k_{1}\)]=\(k_{2}\),· · · R[i] [\(k_{n}\)] =i。
(3)你会惊讶的发现当我们有一个j 时 ,我们就可以由R[i] [j]得到\(k_{1}\) (也就是i,j最小路径上j上一个点), 就可以由R[i] [\(k_{1}\)]得到\(k_{2}\),一直得到 i 。
//下面代码实现由j得到路径所有点。
int tedge=j;
while(tedge!=i){
path[++cnt]=tedge;
tedge=R[i][tedge];
}
path[++cnt]=i;
path[++cnt]=k;
//由与用i作为结束最后还要加上i,见图(1)不能只保存灰色线上的点,还要把k点加上。(4) 那么所有问题就变成确定这个j,如果你把第1个问题(求最小环)理解了那么这里你应该已经很清楚了。就是看每次 ans>dis[i] [j]+e[i] [k]+e[k] [j] 时更新了新的 j。这时你要让cnt=0(cnt是path[]指向下一个添加位置的变量,可以理解未当前存的点个数)这步就相当于删除了path[]里存的之前得路径,然后按(3)步骤重新存路径上的点。最后输出path[]中的点就是路径
//代码注释需要的话私信我补上
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MA=1e3+5;
const int INF=0xfffffff;
int edge[MA][MA];
int dis[MA][MA];
int R[MA][MA];
int path[MA];
int ans;
int cnt;
int n,m;
void init()
{
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
edge[i][j]=dis[i][j]=INF;
R[i][j]=i;
}
}
}
void Floyd()
{
ans=INF;
cnt=0;
for(int k=1;k<=n;++k){
for(int i=1;i<=k;++i){
for(int j=i+1;j<=k;++j){
if(ans>dis[i][j]+edge[i][k]+edge[k][j]){
cnt=0;
ans=dis[i][j]+edge[i][k]+edge[k][j];
int tedge=j;
while(tedge!=i){
path[++cnt]=tedge;
tedge=R[i][tedge];
}
path[++cnt]=i;
path[++cnt]=k;
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]){
dis[i][j]=dis[i][k]+dis[k][j];
R[i][j]=R[k][j];
}
}
}
}
if(ans==INF)printf("No solution.\n");
else{
for(int i=1;i<=cnt;++i)printf("%d%s",path[i],i==cnt?"\n":" ");
}
}
int main()
{
while(~scanf("%d%d",&n,&m)){
init();
for(int i=1;i<=m;++i){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(c>edge[a][b])continue;
edge[a][b]=edge[b][a]=dis[a][b]=dis[b][a]=c;
}
Floyd();
}
return 0;
}
这篇自己感觉说的很细了,应该好理解一些。^ _ ^
学习博客:
https://www.cnblogs.com/DF-yimeng/p/8858184.html(博客园)
https://wenku.baidu.com/view/d1031265657d27284b73f242336c1eb91a373384.html(百度文库)
https://blog.csdn.net/qq_34798152/article/details/77688814(最小环+路径题,代码学习)(poj1734)
最重要的事: 如果发现错误或者有任何问题,任何不理解的地方请评论提出,或私信me,^ _ ^