数据结构专题之链表
介绍
与数组相似,链表也是一种线性数据结构
链表中的每个元素其实为一个单独的对象,而所有对象都通过每个元素中的引用字段链接在一起
单链表
定义
单链表中的每个结点不仅包含值,还包含链接到下一个结点的引用字段。通过这种方式,链表将所有结点按顺序组织起来。

结点结构
// java
// Definition for singly-linked list.
public class SinglyListNode {
int val;
SinglyListNode next;
SinglyListNode(int x) { val = x; }
}
// c++
// Definition for singly-linked list.
struct SinglyListNode {
int val;
SinglyListNode *next;
SinglyListNode(int x) : val(x), next(NULL) {}
};
与数组不一样,无法在常量时间内访问单链表中的随机元素,如果想要获取第 i i i 个元素,只能从头结点开始逐个遍历,按照索引来访问元素平均要花费 O ( N ) O(N) O(N) 的时间,其中 N 是链表长度。
添加
在给定结点之后插入新值
在开头添加结点
头结点代表整个链表,因此在链表开头添加新结点时要注意更新头结点 head
与数组不同,不需要将所有元素移动到插入元素之后。
因此,可以在 O(1) 时间复杂度中将新结点插入到链表中,这非常高效
删除
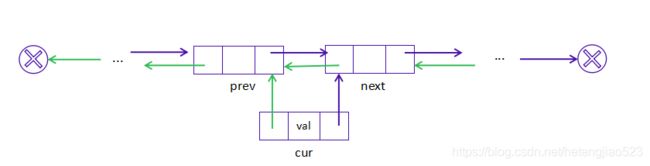
从单链表删除现有结点 cur
- 找到 cur 的上一个结点 prev 和下一个结点 next

- 将 cur 的下一个结点 next 链接到 prev

在第一步中,需要找出 prev 和 next,使用 cur 的参考字段可以很快找出 next,但是必须要从头结点遍历链表,以找出 prev,它的平均时间是 O(N),其中 N 是链表长度。
删除结点的时间复杂度为 O(N), 空间复杂度为 O(1),因为只需用常量空间来存储指针。
删除第一个结点
设计链表
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前结点的值,next 是指向下一个结点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个结点。假设链表中的所有结点都是 0-index 的。
在链表类中实现这些功能:
- get(index):获取链表中第 index 个结点的值。如果索引无效,则返回-1。
- addAtHead(val):在链表的第一个元素之前添加一个值为 val 的结点。插入后,新结点将成为链表的第一个结点。
- addAtTail(val):将值为 val 的结点追加到链表的最后一个元素。
- addAtIndex(index,val):在链表中的第 index 个结点之前添加值为 val 的结点。如果 index 等于链表的长度,则该结点将附加到链表的末尾。如果 index 大于链表长度,则不会插入结点。如果index小于0,则在头部插入结点。
- deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个结点。
示例:
MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3
提示:
- 所有val值都在 [1, 1000] 之内。
- 操作次数将在 [1, 1000] 之内。
- 请不要使用内置的 LinkedList 库。
/* class ListNode {
* int val;
* ListNode next;
* ListNode (int val) {this.val = val;}
*}
*/
class MyLinkedList {
/** Initialize your data structure here. */
ListNode head = null;
public MyLinkedList() {
head = new ListNode(0);
}
/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
public int get(int index) {
ListNode cur = head.next;
int num = -1;
while(cur != null) {
num++;
if(num == index) {
return cur.val;
}
cur = cur.next;
}
return -1;
}
/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
public void addAtHead(int val) {
ListNode node = new ListNode(val);
node.next = head.next;
head.next = node;
}
/** Append a node of value val to the last element of the linked list. */
public void addAtTail(int val) {
ListNode cur = head;
while(cur.next != null) {
cur = cur.next;
}
cur.next = new ListNode(val);
}
/** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
public void addAtIndex(int index, int val) {
ListNode cur = head;
int num = -1;
while(cur != null) {
num++;
if(num == index) {
ListNode node = new ListNode(val);
node.next = cur.next;
cur.next = node;
}
cur = cur.next;
}
}
/** Delete the index-th node in the linked list, if the index is valid. */
public void deleteAtIndex(int index) {
ListNode cur = head;
int num = -1;
while(cur.next != null) {
num++;
if(num == index) {
cur.next = cur.next.next;
break;
}
cur = cur.next;
}
}
}
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList obj = new MyLinkedList();
* int param_1 = obj.get(index);
* obj.addAtHead(val);
* obj.addAtTail(val);
* obj.addAtIndex(index,val);
* obj.deleteAtIndex(index);
*/
链表中的双指针技巧
算法概述
先看一个经典问题:
给定一个链表,判断链表中是否有环。
使用哈希表 可以解决这个问题。
但是,使用 双指针技巧 有一个更有效的解决方案。
想象一下,有两个速度不同的跑步者。如果他们在直路上行驶,快跑者将首先到达目的地。但是,如果它们在圆形跑道上跑步,那么快跑者如果继续跑步就会追上慢跑者。
这正是我们在链表中使用两个速度不同的指针时会遇到的情况:
- 如果没有环,快指针将停在链表的末尾。
- 如果有环,快指针最终将与慢指针相遇。
所以剩下的问题是:
这两个指针的适当速度应该是多少?
一个安全的选择是每次移动慢指针一步,而移动快指针两步。每一次迭代,快速指针将额外移动一步。如果环的长度为 M,经过 M 次迭代后,快指针肯定会多绕环一周,并赶上慢指针。
双指针模板
// c++
// Initialize slow & fast pointers
ListNode* slow = head;
ListNode* fast = head;
/**
* Change this condition to fit specific problem.
* Attention: remember to avoid null-pointer error
**/
while (slow && fast && fast->next) {
slow = slow->next; // move slow pointer one step each time
fast = fast->next->next; // move fast pointer two steps each time
if (slow == fast) { // change this condition to fit specific problem
return true;
}
}
return false; // change return value to fit specific problem
// Java
// Initialize slow & fast pointers
ListNode slow = head;
ListNode fast = head;
/**
* Change this condition to fit specific problem.
* Attention: remember to avoid null-pointer error
**/
while (slow != null && fast != null && fast.next != null) {
slow = slow.next; // move slow pointer one step each time
fast = fast.next.next; // move fast pointer two steps each time
if (slow == fast) { // change this condition to fit specific problem
return true;
}
}
return false; // change return value to fit specific problem
注意事项
- 在调用 next 字段之前,始终检查节点是否为空
获取空结点的下一个结点将导致空指针错误。例如,在我们运行fast = fast.next.next之前,需要检查fast和fast.next不为空。 - 仔细定义循环的结束条件
复杂度分析
空间复杂度分析容易。如果只使用指针,而不使用任何其他额外的空间,那么空间复杂度将是 O(1)。但是,时间复杂度的分析比较困难。为了得到答案,我们需要分析运行循环的次数。
在前面的查找循环示例中,假设我们每次移动较快的指针 2 步,每次移动较慢的指针 1 步。
如果没有循环,快指针需要 N/2 次才能到达链表的末尾,其中 N 是链表的长度。
如果存在循环,则快指针需要 M 次才能赶上慢指针,其中 M 是列表中循环的长度。
显然,M <= N 。所以我们将循环运行 N 次。对于每次循环,我们只需要常量级的时间。因此,该算法的时间复杂度总共为 O(N)。
自己分析其他问题以提高分析能力。别忘了考虑不同的条件。如果很难对所有情况进行分析,请考虑最糟糕的情况。
反转链表
算法概述
先看一个经典问题
反转一个单链表
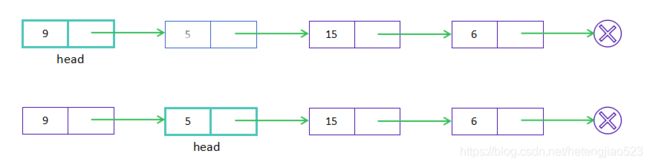
按原始顺序迭代结点,并将他们逐个移动到列表的头部。
看一个例子:
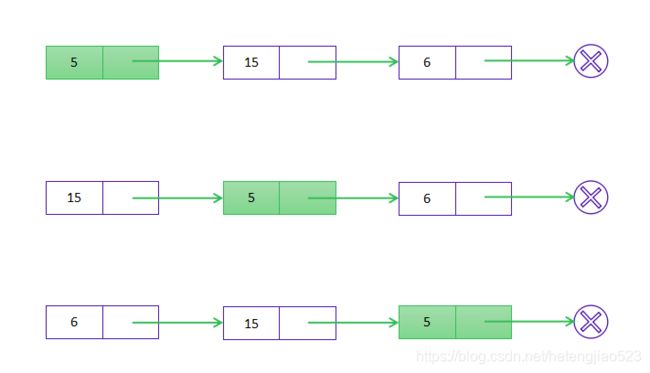
在该算法中,每个结点只移动一次
时间复杂度为 O(N),其中 N 为链表长度
只使用常量级的额外空间,所以,空间复杂度为 O(1)
注意事项
- 同时使用多个指针
- 跟踪当前结点的上一个结点
双链表
定义
双链表以类似单链表的方式工作,但是还有一个引用字段,称为 prev 字段,有了这个字段,就知道了当前结点的前一个结点。

结点结构
// C++
// Definition for doubly-linked list.
struct DoublyListNode {
int val;
DoublyListNode *next, *prev;
DoublyListNode(int x) : val(x), next(NULL), prev(NULL) {}
};
// Java
// Definition for doubly-linked list.
class DoublyListNode {
int val;
DoublyListNode next, prev;
DoublyListNode(int x) {val = x;}
}
添加
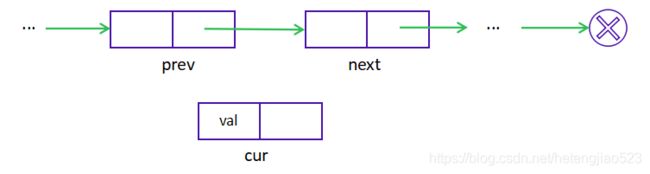
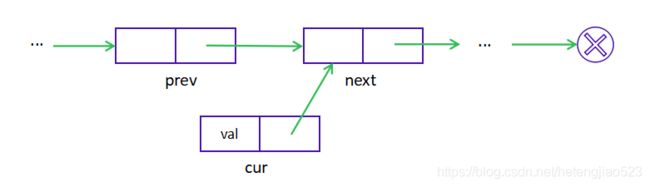
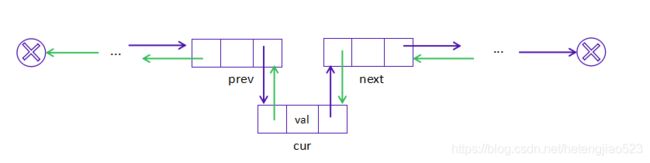
如果要在现有结点 prev 之后填加一个新的结点 cur,可以分为以下两个步骤:
与单链表类似,添加操作的时间和空间复杂度都是 O(1)。
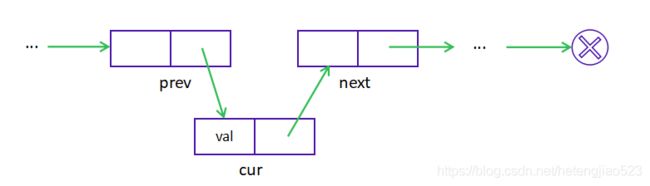
删除
如果我们想从双链表中删除一个现有的结点 cur,我们可以简单地将它的前一个结点 prev 与下一个结点 next 链接起来。
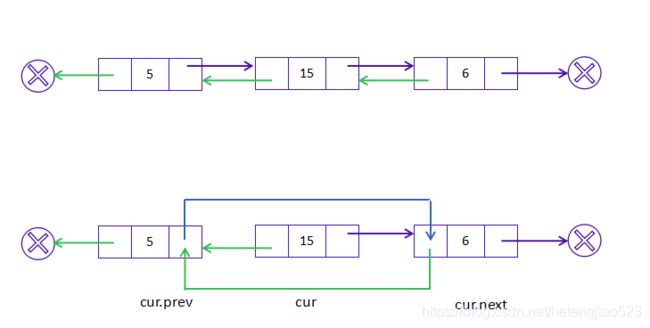
与单链表不同,使用 prev 字段可以很容易地在常量时间内获得前一个结点。
因为我们不再需要遍历链表来获取前一个结点,所以时间和空间复杂度都是 O(1)。
总结
单链表和双链表
它们在许多操作中是相似的。
- 它们都无法在常量时间内随机访问数据。
- 它们都能够在 O(1) 时间内在给定结点之后或列表开头添加一个新结点。
- 它们都能够在 O(1) 时间内删除第一个结点。
但是删除给定结点(包括最后一个结点)时略有不同。
- 在单链表中,它无法获取给定结点的前一个结点,因此在删除给定结点之前我们必须花费 O(N) 时间来找出前一结点。
- 在双链表中,这会更容易,因为我们可以使用“prev”引用字段获取前一个结点。因此我们可以在 O(1) 时间内删除给定结点。
对照
链表和其他数据结构(包括数组,队列和栈)之间时间复杂度的比较:
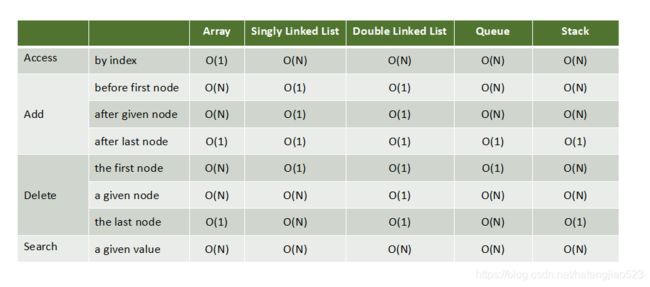
结论:
-
如果你需要经常添加或删除结点,链表可能是一个不错的选择。
-
如果你需要经常按索引访问元素,数组可能是比链表更好的选择。
附录:经典用例
环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
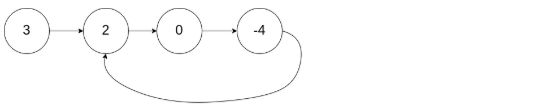
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode l1 = head;
ListNode l2 = head;
while(l1 != null && l2 != null && l2.next != null) {
if(l1 == l2.next) {
return true;
}
l1 = l1.next;
l2 = l2.next.next;
}
return false;
}
}
环形链表II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode f = head;
ListNode s = head;
while(f != null && f.next != null) {
s = s.next;
f = f.next.next;
if(s == f) {
break;
}
}
if(f == null || f.next == null) {
return null;
}
s = head;
while (s != f) {
s = s.next;
f = f.next;
}
return s;
}
}
相交链表
编写一个程序,找到两个单链表相交的起始节点。
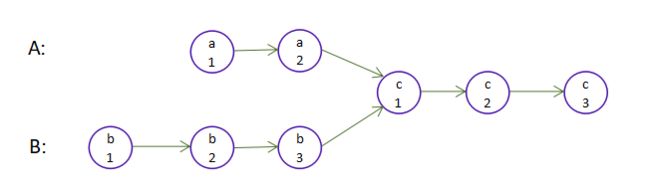
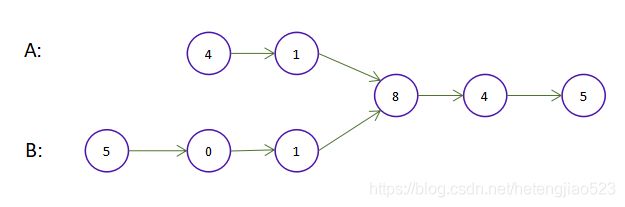
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
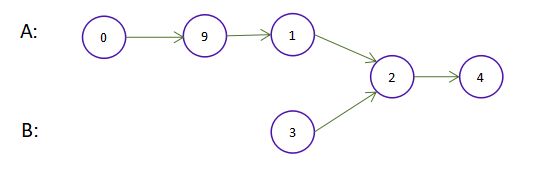
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
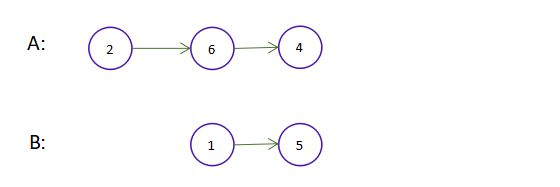
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
- 如果两个链表没有交点,返回 null.
- 在返回结果后,两个链表仍须保持原有的结构。
- 可假定整个链表结构中没有循环。
- 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
//方法一:遍历链表,到达末尾之后,指向另一个链表的头部,这二次循环的时候,长度差消失,同时到达相交节点
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null || headB == null) return null;
ListNode pA = headA;
ListNode pB = headB;
while(pA != pB){
pA = pA==null ? headB : pA.next;
pB = pB==null ? headA : pB.next;
}
return pA;
}
}
//方法二:遍历链表,分别找到两个链表的长度,然后让长的链表比短链表先开始走len(L) - len(S) 步,然后开始同时遍历
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode pL = headA;
ListNode pS = headB;
int lenA = 0;
while(pL != null){
lenA++;
pL = pL.next;
}
int lenB = 0;
while(pS != null){
lenB++;
pS = pS.next;
}
pL = headA;
pS = headB;
int len = lenA - lenB;
if(len < 0){
//单链表B是长的
pL = headB;
pS = headA;
len = lenB - lenA;
}
//最长的单链表永远是pL,并且差值len是一个正数
for(int i = 0;i < len; i++){
pL = pL.next;
}
//pL和pS在同一个起跑线上
while(pL != null && pS != null && pL != pS){
pL = pL.next;
pS = pS.next;
}
if(pL == pS && pL != null && pS != null ){
return pL;
}
return null;
}
}
删除链表的倒数第N个节点
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if(head == null) {
return head;
}
ListNode p1 = head;
ListNode p2 = head;
while(n-- != 0) {
p2 = p2.next;
}
if(p2 == null) {
return p1.next;
}
while(p2.next != null) {
p1 = p1.next;
p2 = p2.next;
}
p1.next = p1.next.next;
return head;
}
}
反转链表
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) {
return head;
}
ListNode prev = null;
ListNode cur = head;
while(cur != null) {
ListNode temp = cur.next;
cur.next = prev;
prev = cur;
cur = temp;
}
return prev;
}
}
移除链表元素
删除链表中等于给定值 val 的所有节点。
示例:
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
//创建虚拟头节点
public ListNode removeElements2(ListNode head, int val) {
ListNode node = new ListNode(-1);
node.next = head;
ListNode prev = node;
while(prev.next != null) {
if(prev.next.val == val) {
prev.next = prev.next.next;
} else {
prev = prev.next;
}
}
return node.next;
}
//递归
public ListNode removeElements(ListNode head, int val) {
if(head == null) {
return null;
}
head.next = removeElements(head.next, val);
return head.val == val ? head.next : head;
}
}
奇偶链表
给定一个单链表,把所有的奇数节点和偶数节点分别排在一起。请注意,这里的奇数节点和偶数节点指的是节点编号的奇偶性,而不是节点的值的奇偶性。
请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1),时间复杂度应为 O(nodes),nodes 为节点总数。
示例 1:
输入: 1->2->3->4->5->NULL
输出: 1->3->5->2->4->NULL
示例 2:
输入: 2->1->3->5->6->4->7->NULL
输出: 2->3->6->7->1->5->4->NULL
说明:
- 应当保持奇数节点和偶数节点的相对顺序。
- 链表的第一个节点视为奇数节点,第二个节点视为偶数节点,以此类推。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode oddEvenList(ListNode head) {
if(head == null) {
return null;
}
ListNode odd = head;
ListNode even = head.next;
ListNode evenHead = even;
while(even != null && even.next != null) {
odd.next = even.next;
odd = odd.next;
even.next = odd.next;
even = even.next;
}
odd.next = evenHead;
return head;
}
}
回文链表
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
}
}
合并两个有序链表
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode l3 = new ListNode(-1);
ListNode res = l3;
while(l1 != null && l2 != null) {
if(l1.val > l2.val) {
l3.next = l2;
l2 = l2.next;
} else {
l3.next = l1;
l1 = l1.next;
}
l3 = l3.next;
}
if(l1 != null) {
l3.next = l1;
}
if(l2 != null) {
l3.next = l2;
}
return res.next;
}
}
回文链表
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
解题思路:
思路1
- 遍历链表,用数组存下每个节点的值,然后从数组两头开始向中间遍历,是否相等
- 时间复杂度O(n),空间复杂度O(n)
思路2
- 遍历一遍链表,得到链表长度n
- 根据长度的奇偶,找到中间节点,将左半边的链表反转
- 然后从中间节点分两个方向向左右两边遍历,是否是回文
- 对左半部分链表进行反转,还原为最初的链表
- 只需要固定的若干个临时变量,不需要额外开辟空间
- 时间复杂度为O(n),空间复杂度为O(1)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
boolean isPalindrome = true;
if(head == null || head.next == null) {
return isPalindrome;
}
int len = 0;
ListNode cur = head;
while(cur != null) {
cur = cur.next;
len++;
}
cur = head;
ListNode prev = null;
for(int i = 0; i < len / 2; i++) {
ListNode temp = cur.next;
cur.next = prev;
prev = cur;
cur = temp;
}
ListNode mid = cur;
ListNode left = prev;
ListNode right = len % 2 == 0 ? mid : mid.next;
while(left != null && right != null) {
if(left.val != right.val) {
isPalindrome = false;
break;
}
left = left.next;
right = right.next;
}
cur = prev;
prev = mid;
for(int i = 0; i < len / 2; i++) {
ListNode temp = cur.next;
cur.next = prev;
prev = cur;
cur = temp;
}
return isPalindrome;
}
}
合并两个有序链表
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode l3 = new ListNode(-1);
ListNode res = l3;
while(l1 != null && l2 != null) {
if(l1.val > l2.val) {
l3.next = l2;
l2 = l2.next;
} else {
l3.next = l1;
l1 = l1.next;
}
l3 = l3.next;
}
if(l1 != null) {
l3.next = l1;
}
if(l2 != null) {
l3.next = l2;
}
return res.next;
}
}
两数相加
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int carray = 0;
ListNode temps = new ListNode(-1);
ListNode res = temps;
while(l1 != null || l2 != null) {
int val1 = l1 == null ? 0 : l1.val;
int val2 = l2 == null ? 0 : l2.val;
int temp = val1 + val2 + carray;
temps.next = new ListNode(temp % 10);
carray = temp / 10;
l1 = l1 == null ? null : l1.next;
l2 = l2 == null ? null : l2.next;
temps = temps.next;
}
if(carray > 0) {
temps.next = new ListNode(carray);
}
return res.next;
}
}
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
//head := new(ListNode)
head := ListNode {
Val : 0,
}
var l *ListNode = &head
carry := 0
//sum := make([]int,0)
for l1 != nil || l2 != nil {
var x, y int
if l1 != nil {
x = l1.Val
l1 = l1.Next
} else {
x = 0
}
if l2 != nil {
y = l2.Val
l2 = l2.Next
} else {
y = 0
}
sum := x + y + carry
carry = sum / 10
l.Next = &ListNode {
Val : sum % 10,
}
l = l.Next
//sum.append(l1.Val + )
}
if carry > 0 {
l.Next = &ListNode {
Val : carry,
}
}
return head.Next
}
旋转链表
给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例 2:
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode rotateRight(ListNode head, int k) {
if(head == null || head.next == null) {
return head;
}
ListNode p = head;
int len = 0;
while(p != null) {
len++;
p = p.next;
}
k = k % len - 1;
if(k < 0) {
return head;
}
ListNode fast = head;
ListNode prev = null;
ListNode cur = head;
while(fast != null && fast.next != null) {
while(k-- > 0) {
fast = fast.next;
}
prev = cur;
fast = fast.next;
cur = cur.next;
}
fast.next = head;
prev.next = null;
return cur;
}
}
复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的深拷贝。
示例:
输入:
{“KaTeX parse error: Expected '}', got 'EOF' at end of input: …":"1","next":{"id”:“2”,“next”:null,“random”:{“KaTeX parse error: Expected 'EOF', got '}' at position 9: ref":"2"}̲,"val":2},"rand…ref”:“2”},“val”:1}
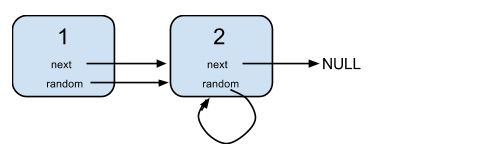
解释:
节点 1 的值是 1,它的下一个指针和随机指针都指向节点 2 。
节点 2 的值是 2,它的下一个指针指向 null,随机指针指向它自己。
提示:
- 你必须返回给定头的拷贝作为对克隆列表的引用。
思路:
- 在原链表中插入“影子节点”
- 根据原节点random 更新影子节点的random
- 分离原链表和“影子链表”,该链表即为深度拷贝的链表
/*
// Definition for a Node.
class Node {
public int val;
public Node next;
public Node random;
public Node() {}
public Node(int _val,Node _next,Node _random) {
val = _val;
next = _next;
random = _random;
}
};
*/
class Solution {
public Node copyRandomList(Node head) {
if(head == null) {
return head;
}
Node p = head;
// 1.新节点接到原对应节点的后面
while(p != null) {
Node clone = new Node(p.val);
clone.next = p.next;
p.next = clone;
p = clone.next;
}
//2.参照原节点的random,改变新节点的rondom
p = head;
while(p != null) {
p.next.random = p.random == null ? null : p.random.next;
p = p.next.next;
}
//3.将两部分分离
p = head;
Node cloneHead = head.next;
Node cloneNode = cloneHead;
while(p != null){
p.next = cloneNode.next;
if(cloneNode.next != null){
cloneNode.next = cloneNode.next.next;
}
p = p.next;
cloneNode = cloneNode.next;
}
return cloneHead;
}
}
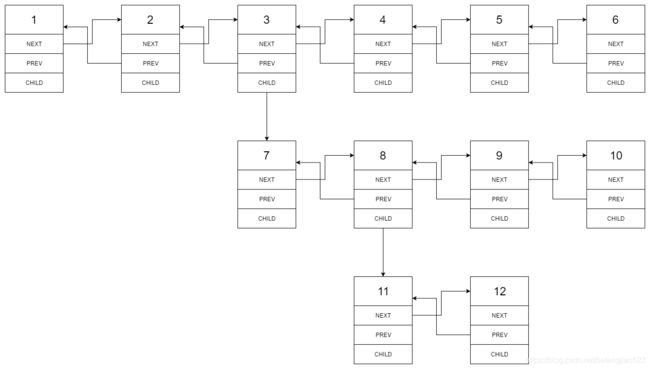
扁平化多级双向链表
您将获得一个双向链表,除了下一个和前一个指针之外,它还有一个子指针,可能指向单独的双向链表。这些子列表可能有一个或多个自己的子项,依此类推,生成多级数据结构,如下面的示例所示。
扁平化列表,使所有结点出现在单级双链表中。您将获得列表第一级的头部。
示例:
输入:
1—2---3—4---5—6–NULL
|
7—8---9—10–NULL
|
11–12–NULL
输出:
1-2-3-7-8-11-12-9-10-4-5-6-NULL
以上示例的说明:
迭代法
/*
// Definition for a Node.
class Node {
public int val;
public Node prev;
public Node next;
public Node child;
public Node() {}
public Node(int _val,Node _prev,Node _next,Node _child) {
val = _val;
prev = _prev;
next = _next;
child = _child;
}
};
*/
class Solution {
public Node flatten(Node head) {
if(head == null) {
return head;
}
Node res = head;
for (Node p = head; p != null; p = p.next) {
Node n = p.next;
if(p.child != null) {
Node c = p.child;
p.next = c;
c.prev = p;
p.child = null;
Node t = c;
while(t != null && t.next != null) {
t = t.next;
}
t.next = n;
if(n != null) {
n.prev = t;
}
}
}
return head;
}
}
递归法
/*
// Definition for a Node.
class Node {
public int val;
public Node prev;
public Node next;
public Node child;
public Node() {}
public Node(int _val,Node _prev,Node _next,Node _child) {
val = _val;
prev = _prev;
next = _next;
child = _child;
}
};
*/
class Solution {
public Node flatten(Node head) {
if(head == null) {
return head;
}
if(head.child == null) {
head.next = flatten(head.next);
} else {
Node n = flatten(head.next);
Node c = head.child;
head.child = null;
c = flatten(c);
c.prev = head;
head.next = c;
Node p = c;
while(c != null && c.next != null) {
c = c.next;
}
c.next = n;
if(n != null) {
n.prev = c;
}
}
return head;
}
}