非递归,不用栈实现二叉树中序遍历
最近总有人问这个问题:“如何不用栈,也不用递归来实现二叉树的中序遍历”。这个问题的实现就是迭代器问题,无论是Java还是C++,利用迭代器遍历树节点(Java中是TreeMap类,C++中是map类)都使用了中序遍历,且无法使用递归和栈,算法效率近似为O(1),不可能每个节点只访问一次。
纯C实现的办法很简单,先定义类型。
// 定义byte_t类型
typedef unsigned char byte_t;
// 定义bool类型
typedef unsigned char bool;
#define true 1
#define false 0// 定义用于比较的函数指针类型
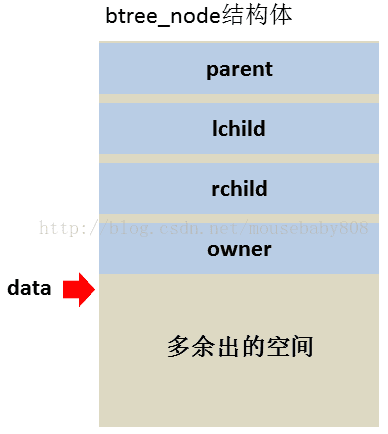
typedef int(*treeset_compare_t)(const void*, const void*);下面结构体中的data[0]是C语言一种特殊用法,data[0]本身不表示任何大小,可以看作是一个指针,表明该结构体在内存中占据的实际大小会超过结构体本身的字节数,这样,data指针就自动指向结构体中多余的空间,该空间可以用来存储节点值。并不是所有的C编译器都能这么做,但我测试过好像就VC++6不行,这段代码在GCC下编译通过。
/**
* 定义二叉树节点类型
*/
typedef struct _btree_node
{
struct _btree_node* parent; // 指向父节点的指针
struct _btree_node* lchild; // 指向左孩子的指针
struct _btree_node* rchild; // 指向右孩子的指针
struct _treeset* owner; // 节点所属的树
byte_t data[0];
} btree_node;/**
* 定义二叉树结构体
*/
typedef struct _treeset
{
struct _btree_node* root; // 二叉树根节点
size_t count; // 二叉树节点数量
size_t elemsize;
treeset_compare_t compare;
} treeset;
定义了以上类型,就可以进一步完成二叉树初始化以及节点添加,删除,查找等函数了,函数声明如下。
/**
* 初始化二叉树结构体
* @param tree 指向二叉树结构体的指针
* @param elemsize 每个元素的大小
* @param comp 用于比较的函数指针
*/
void treeset_init(treeset* tree, size_t elemsize, treeset_compare_t comp);
/**
* 释放二叉树占据的空间
* @param tree 指向二叉树结构体的指针
*/
void treeset_free(treeset* tree);
/**
* 向二叉树中添加元素
* @param tree 指向二叉树结构体的指针
* @param value 指向要添加元素的指针
* @return 是否实际添加了节点
*/
bool treeset_add(treeset* tree, const void* value);
/**
* 从二叉树中删除一个元素
* @param tree 指向二叉树结构体的指针
* @param value 要删除的节点内容
* @return 是否删除了节点
*/
bool treeset_remove(treeset* tree, const void* value);
/**
* 在二叉树中查找一个元素
* @param tree 指向二叉树结构体的指针
* @param value 指向要查找内容的指针
* @return 是否包含要查询的值
*/
bool treeset_contain(const treeset* tree, const void* value);这部分函数实现如下:
下面这个函数用于初始化二叉树,其中参数elemsize表示每个树节点要存放的值所占内存大小,例如每个节点要保存一个整数,则elemsize的值应该为sizeof(int),这个大小将直接反映在每个树节点上,由节点结构体分量data来表示。comp参数是一个函数指针,前面定义过,用来表示比较两个值的大小。
/**
* 初始化二叉树结构体
* @param tree 指向二叉树结构体的指针
* @param elemsize 每个元素的大小
* @param comp 用于比较的函数指针
*/
void treeset_init(treeset* tree, size_t elemsize, treeset_compare_t comp)
{
tree->root = NULL;
tree->count = 0;
// 设置节点存储的元素大小
tree->elemsize = elemsize;
// 设置用于元素大小比较的函数指针
tree->compare = comp;
}/**
* 释放二叉树占据的空间
* @param tree 指向二叉树结构体的指针
*/
void treeset_free(treeset* tree)
{
// 从头节点开始移除二叉树中所有的节点
remove_all_node(tree->root);
// 将二叉树所有内容还原为空
memset(tree, 0, sizeof(*tree));
}/**
* 向二叉树中添加元素
* @param tree 指向二叉树结构体的指针
* @param value 指向要添加元素的指针
* @return 是否实际添加了节点
*/
int treeset_add(treeset* tree, const void* value)
{
int result = 0;
// 判断二叉树中是否有头节点
if (tree->count == 0)
{
// 创建头节点
tree->root = create_new_node(tree, value);
result = 1;
}
else
{
/*
对于添加节点,具体操作如下:
1. 通过要添加节点的值和现有某个节点(从头节点开始)进行比较(通过指定的比较函数进行)
2. 如果要添加的节点值和现有某个节点值相同,则无需添加节点
3. 如果要添加的节点值和现有某个节点值不同,则根据比较结果继续访问该节点的左支或者右支
添加流程示意图参看[图1]
*/
// 表示比较结果
int comp;
// node变量指向要比较的节点,从头结点开始;parent变量指向其父节点
btree_node* node = tree->root, *parent;
// 遍历所有节点,直到没有节点为止
while (node)
{
// 保存父节点指针
parent = node;
// 比较要添加的值和当前节点值
comp = tree->compare(value, node + 1);
// 判断比较结果
if (comp == 0)
break; // 节点值与要添加的值相同,停止流程
if (comp > 0)
node = node->rchild; // 要添加的值大于节点值,继续访问当前节点的右支
else
node = node->lchild; // 要添加的值小于节点值,继续访问当前节点的左支
}
// 如果循环结束且比较结果不为0,表示整个树中没有和要添加节点值相同的节点,需要通过添加新节点来保存改值
if (comp != 0)
{
// 创建新的节点并保存节点值
node = create_new_node(tree, value);
// 为新节点设置父节点,为遍历结束时最后一个有效节点
node->parent = parent;
// 根据比较结果设置新节点的位置
if (comp > 0)
parent->rchild = node; // 新节点值大于最后一个树节点值,添加为该树节点的右孩子
else
parent->lchild = node; // 新节点值小于最后一个树节点值,添加为该树节点的左孩子
result = 1;
}
}
// 修改节点数
tree->count++;
// 返回已添加的节点
return result;
}下面这个函数用于从二叉树中删除一个节点,删除的步骤较为复杂,分为两种情况,先读懂图例,代码就很好理解了。代码中的find_node函数后面介绍:
/**
* 从二叉树中删除一个元素
* @param tree 指向二叉树结构体的指针
* @param value 要删除的节点内容
* @return 是否删除了节点
*/
int treeset_remove(treeset* tree, const void* value)
{
// 根据要删除的节点值查找要删除的节点
btree_node* node = find_node(tree, value);
// 判断是否找到要删除的节点
if (node)
{
/*
对于删除节点,具体操作如下:
1. 判断要删除的节点情况:(1)是否同时具备左右支 (2) 是否只具备左支或右支
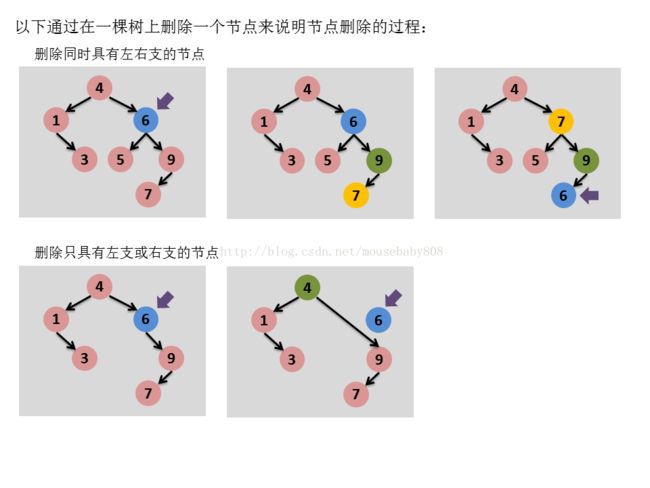
2. 对于情况(1),需要将要删除节点的值和该节点右孩子的左支最末节点值进行交换(参加图2),确保交换后二叉树仍保持正确结构,将问题转为情况(2)
3. 对于情况(2),只需要将要删除节点的父节点和要删除节点的子节点(左支或右支)建立关系,让要删除节点脱离树结构即可
4. 对于要删除节点没有子节点的情况,只需要让被删除节点的父节点失去左孩子(或右孩子)即可
添加流程示意图参看[图2]
*/
// 用于临时保存节点
btree_node* temp;
// 判断要删除的节点是否同时具有左支和右支
if (node->rchild && node->lchild)
{
// 找到比要删除节点值大的最小值,即节点右孩子的左支最末节点(也可以找必要删除节点值小的最大值)
temp = node->rchild;
while (temp->lchild)
temp = temp->lchild;
// 将上一步找到节点的值复制到要删除的节点中
memcpy(node + 1, temp + 1, tree->elemsize);
// 将要删除节点指针重新指向前面找到的节点,此时要删除的节点将不再同时具备左右支
node = temp;
}
// 找到要删除节点的左支或者右支
temp = node->lchild ? node->lchild : node->rchild;
// 判断要删除节点是否具备左支或者右支
if (temp)
{
/*
* 建立要删除节点父节点和要删除节点左支(或右支)的联系,排除掉要删除节点
*/
// 将被删除节点孩子的父节点改为被删除节点的父节点。即越过被删除节点,建立被删除节点上一代和下一代的直接联系
temp->parent = node->parent;
// 判断要删除的是否为头节点
if (node->parent)
{
// 判断要删除的节点是其父节点的左支或右支
if (node == node->parent->lchild)
node->parent->lchild = temp; // 若要删除节点是其父节点的左孩子,则将其孩子节点设置为其父节点的左支
else
node->parent->rchild = temp; // 若要删除节点是其父节点的右孩子,则将其孩子节点设置为其父节点的右支
}
else
tree->root = temp; // 将被删除节点的孩子节点设置为头节点
}
else
{
/*
* 如果要删除的节点是一个叶节点(即没有孩子的节点),则将该节点的父节点与该节点相关的左支或右支联系删除即可
*/
// 判断要删除的节点是否为头节点
if (node->parent)
{
// 判断要删除的节点是其父节点的左支或右支
if (node == node->parent->lchild)
node->parent->lchild = NULL; // 若要删除节点是其父节点的左孩子,则将其孩子节点设置空
else
node->parent->rchild = NULL; // 若要删除节点是其父节点的右孩子,则将其孩子节点设置空
}
else
tree->root = NULL; // 将头节点设置为空,此时表示最后一个节点被删除,树变为空树
}
// 释放节点所占内存
free(node);
// 修改二叉树节点总数
tree->count--;
}
// 返回是否创建了新节点
return node != NULL;
}下面的函数用于在树中查找一个节点,用到的find_node在后面介绍
/**
* 在二叉树中查找一个元素
* @param tree 指向二叉树结构体的指针
* @param value 指向要查找内容的指针
* @return 是否包含要查询的值
*/
int treeset_contain(const treeset* tree, const void* value)
{
// 返回是否能找到指定节点
return find_node(tree, value) != NULL;
}代码中用到的几个子函数如下:
create_new_node用于创建一个节点,该节点可以容纳btree_node结构体内容和额外的节点值内容:
/**
* 创建一个新的树节点
* @param owner 节点所属的树结构体指针
* @param value 要存放在结点中的内容指针
* @return 返回树节点指针
*/
static btree_node* create_new_node(treeset* owner, const void* value)
{
// 分配节点内存,大小为节点大小加上要存储元素值的大小
btree_node* pn = (btree_node*)malloc(sizeof(btree_node) + owner->elemsize);
// 设置节点分量值
pn->lchild = pn->rchild = pn->parent = NULL;
// 设置节点所属的树
pn->owner = owner;
// 将节点值复制到指定的节点中
memcpy(pn + 1, value, sizeof(owner->elemsize));
// 返回创建的节点
return pn;
}remove_all_node用于删除某个节点及其子节点,如果传入根节点,则删除整棵树
/**
* 删除所有的节点
* @param node 节点指针
* @note 该函数利用递归的方式对接点进行删除
*/
static void remove_all_node(btree_node* node)
{
if (node)
{
// 递归调用删除指定节点的左支
remove_all_node(node->lchild);
// 递归调用删除指定节点的右支
remove_all_node(node->rchild);
// 删除当前节点
free(node);
}
}
find_node用于查找一个节点,依然是利用一边小一边大的原则来进行:
/**
* 在二叉树中查找一个元素
* @param tree 指向二叉树结构体的指针
* @param value 指向要查找内容的指针
* @return 找到的节点
*/
static btree_node* find_node(const treeset* tree, const void* value)
{
// 先取得头节点
btree_node* node = tree->root;
// 遍历,直到无节点可访问
while (node)
{
// 利用比较函数比较节点存储内容和待查找内容
int cmp = tree->compare(value, node + 1);
if (cmp == 0)
break; // 查找结束,已找到所需节点
if (cmp > 0)
node = node->rchild; // 待查元素值比节点存储值大,则进一步查找节点的右支
else
node = node->lchild; // 待查元素值比节点存储值小,则进一步查找节点的左支
}
// 返回查询到的节点
return node;
}好了,有了上述代码,树就可以发挥作用了,现在重点讲一下如何中序遍历这棵树且不用递归和栈(使用递归的方法很简单,使用栈的方法网上也有一些,大家可以自行查找),即使用迭代器的方法遍历节点:
首先,定义迭代器结构体,很简单,只有一个节点指针存放当前访问的节点:
/**
* 定义迭代器
*/
typedef struct
{
btree_node* cur; // 当前迭代到的节点指针
} treeset_iterator;有了这个结构体,就可以实现如下几个迭代器访问函数:
/**
* 针对二叉树初始化迭代器
* @param tree 指向二叉树结构体的指针
* @param iter 指向迭代器结构体变量的指针
*/
void treeset_iterator_init(const treeset* tree, treeset_iterator* iter);
/**
* 查看是否有下一个节点
* @param iter 指向迭代器结构体变量的指针
*/
int treeset_iterator_hasmore(const treeset_iterator* iter);
/**
* 令迭代器指向下一个位置
* @param iter 指向迭代器结构体变量的指针
* @param value 输出一个值
*/
int treeset_iterator_next(treeset_iterator* iter, void* value);上述几个函数实现如下:
treeset_iterator_init用于初始化迭代器,令迭代器中的节点指针指向整棵树中最左边的节点。
/**
* 针对二叉树初始化迭代器
* @param tree 指向二叉树结构体的指针
* @param iter 指向迭代器结构体变量的指针
*/
void treeset_iterator_init(const treeset* tree, treeset_iterator* iter)
{
// 获取二叉树头节点
btree_node* node = tree->root;
// 移动指针,指向整个二叉树最左边(值最小)的节点
while (node->lchild)
node = node->lchild;
// 将找到的节点指针保存在迭代器中
iter->cur = node;
}treeset_iterator_hasmore函数用于判断是否还能继续访问下一个节点
/**
* 查看是否有下一个节点
* @param iter 指向迭代器结构体变量的指针
*/
int treeset_iterator_hasmore(const treeset_iterator* iter)
{
// 返回迭代器是否还有下一个节点
return iter->cur != NULL;
}
treeset_iterator_next函数用于获取当前节点的值并移动到下一个节点,移动的步骤较为复杂,请参看图例。访问的整个过程就是一个访问和回朔的过程
/**
* 令迭代器指向下一个位置
* @param iter 指向迭代器结构体变量的指针
* @param value 输出一个值
*/
int treeset_iterator_next(treeset_iterator* iter, void* value)
{
btree_node* node = iter->cur;
// 判断迭代是否结束
if (!node)
return 0;
/*
节点的迭代
对于一个二叉树来说,总有一种方法可以依次访问树中的所有节点,但和线性结构不同,要遍历树中所有节点,必须按照一种规则和步骤:
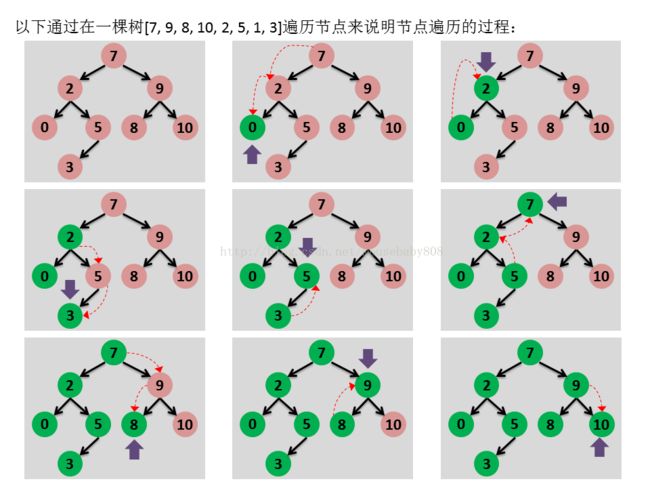
1. 在开始遍历前,先用指针指向整个树中最左边的节点(即树中值最小的节点),以此作为遍历的起点;
2. 每次总以当前节点右孩子的左支的最末节点作为迭代的下一个节点,该节点必然为比当前节点值大的最小值节点;
3. 如果当前节点没有右孩子,则访问其父节点,并将不以当前节点为右孩子的父节点作为下一个节点
4. 如果在第3步得到NULL值,表示整个遍历结束
遍历流程参考[图3]
*/
// 保存节点值
memcpy(value, node + 1, node->owner->elemsize);
// 判断当前节点是否有右孩子
if (node->rchild) // 有右孩子的情况
{
// 令指针指向当前节点的右孩子(如果该节点没有左支,则该节点就作为迭代的下一个节点)
node = node->rchild;
// 通过循环令指针指向该节点左支的最末节点,该节点为迭代的下一个节点
while (node->lchild)
node = node->lchild;
}
else // 没有右孩子的情况
{
btree_node* temp;
// 向上访问当前节点的父节点
do
{
temp = node;
node = node->parent;
} while (node && temp == node->rchild); // 依次访问当前节点的父节点,直到没有父节点(到达头节点)或者当前节点不是其父节点的右孩子
}
// 将当前迭代到的节点保存在迭代器中
iter->cur = node;
return 1;
}好了,以上的代码即可完成所需的遍历访问,可以用如下代码进行测试:
/**
* 用于比较两个int值的函数
* @param a 指向第一个int值的指针
* @param b 指向第二个int值的指针
* @return 0表示两个值相同,正数表示a较大,负数表示b较大
*/
static int int_compare(const int* a, const int* b)
{
return *a - *b;
}
/**
* 中序遍历显示二叉树内容
* @param tree 指向二叉树结构体的指针
*/
static void show_tree(const treeset* tree)
{
// 定义分隔符
const char* spliter = "";
// 定义一个迭代器
treeset_iterator iter;
// 保存值的变量
int value;
printf(" 集合节点为:");
// 初始化迭代器
treeset_iterator_init(tree, &iter);
// 遍历直到访问了所有的树节点
while (treeset_iterator_hasmore(&iter))
{
// 获取当前节点,令迭代器指向下一个节点
treeset_iterator_next(&iter, &value);
// 输出当前节点值
printf("%s%d", spliter, value);
spliter = ",";
}
printf("\n 元素总数%d\n", tree->count);
}
// 用于测试的数值
static int VALS[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20};
int main()
{
int n;
// 定义一个树结构
treeset set;
#ifdef DEBUG
// 在程序结束时显示内存报告
atexit(show_block);
#endif // DEBUG
// 设置随机数种子
srand(time(0));
// 利用随机数打乱数组内容
for (n = 0; n < 1000; n++)
{
int a = rand() % (sizeof(VALS) / sizeof(VALS[0]));
int b = rand() % (sizeof(VALS) / sizeof(VALS[0]));
if (a != b)
{
VALS[a] ^= VALS[b];
VALS[b] ^= VALS[a];
VALS[a] ^= VALS[b];
}
}
// 初始化树结构
treeset_init(&set, sizeof(int), (treeset_compare_t)int_compare);
// 存储元素
printf("测试元素存储\n");
for (n = 0; n < sizeof(VALS) / sizeof(VALS[0]); n++)
treeset_add(&set, &VALS[n]);
printf(" 二叉树中存放了%d个元素\n", set.count);
show_tree(&set);
puts("");
// 查找元素
printf("测试元素查询:\n");
for (n = 0; n < 10; n++)
{
int a = rand() % 50;
if (treeset_contain(&set, &a))
printf(" 元素%d已存在\n", a);
else
printf(" 元素%d不存在\n", a);
}
puts("");
// 测试元素删除
printf("测试元素删除\n");
n = rand() % 20 + 1;
printf(" 删除前元素%d%s\n", n, treeset_contain(&set, &n) ? "存在" : "不存在");
treeset_remove(&set, &n);
printf(" 删除后元素%d%s\n", n, treeset_contain(&set, &n) ? "存在" : "不存在");
n = rand() % 20 + 1;
printf(" 删除前元素%d%s\n", n, treeset_contain(&set, &n) ? "存在" : "不存在");
treeset_remove(&set, &n);
printf(" 删除后元素%d%s\n", n, treeset_contain(&set, &n) ? "存在" : "不存在");
show_tree(&set);
// 释放树结构
treeset_free(&set);
return 0;
}
其中重点关注show_tree函数,该函数即利用迭代器完成了二叉树的遍历,且无需任何递归和栈的辅助,且迭代器的访问可以随时暂停或继续,非常灵活方便。