状态压缩dp——学习笔记
首先学习位运算的有关知识,掌握了的可以下翻。
与运算
and运算通常用于二进制的取位操作,例如一个数 and 1的结果就是取二进制的最末位。这可以用来判断一个整数的奇偶,二进制的最末位为0表示该数为偶数,最末位为1表示该数为奇数。
或运算
非运算
not运算的定义是把内存中的0和1全部取反。使用not运算时要格外小心,你需要注意整数类型有没有符号。如果not的对象是无符号整数(不能表示负数),那么得到的值就是它与该类型上界的差,因为无符号类型的数是用00到$FFFF依次表示的。下面的两个程序(仅语言不同)均返回65435。
左移&右移
左移运算
异或运算
异或的符号是^。按位异或运算, 对等长二进制模式按位或二进制数的每一位执行逻辑按位异或操作. 操作的结果是如果某位不同则该位为1, 否则该位为0.
判断数字x第i位是否为1,if(x&(1<
将一个数字x第i位改成1,x|=(1<
首先来一个例题,大名鼎鼎的旅行商问题:
旅行商问题
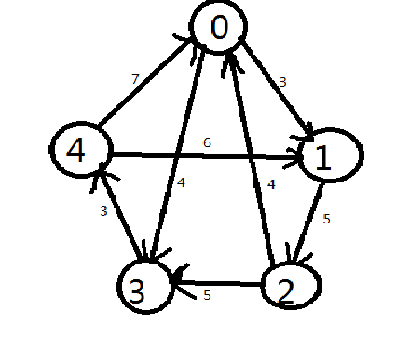
给定一个n个顶点组成的带权有向图的距离矩阵d(I,j)(INF表示没有边)。要求从顶点0出发,经过每个定点恰好一次后再回到顶点0。问所经过的边的总权重的最小值是多少?
限制条件:2≤n≤5 , 0≤d(i,j)≤1000;输入:n=5;
手工制图(5毛钱绘图)
输出:22(0->3->4->1->2->0)
这就是著名的旅行商问题,但现今没有一个高效的算法可以解决这一问题。
所有可能的路线为(n-1)!种,推出这个我们可以设想一下,
有3个点时,路径为2种;
有4个点时,路径为6种(沙漏形4种,正方2种)(注意反向可行)
有5个点时,路径为24种(比较麻烦,意会一下)
这样我们可以找一下规律得到(n-1)!种路径;这是一个非常大的值,即使n在样例之中已经很小了,所有情况还是不能一一枚举。
假设现在已经访问过的顶点的集合(起点0当做未访问过的顶点)为S,当前访问过的顶点为v,dp[S][v]表示从v出发访问剩余的所有顶点,最终回到顶点0路径的权重总和最小值。u表示要访问的那个点。
递推式我们可以得到:
dp[V][0]=0;
dp[S][v]=min{dp[S∪{u}][u]+d[v][u]};(由于从v出发可以移动到任意一个节点u∉S)
因为这个递推式中,下标有集合而不是整数,因此需要处理,把这个状态压缩成一个整数,这就是状压dp的名字由来~~
那么,我们怎么样处理呢?
方法1:记忆化搜索:
我们可以将下标为集合的编码成一个整数,或者利用中序二叉树存储;我们采用的方法是将每一个元素的选取对应到一个二进制位中去!!
伪代码如下:
//输入
int dp[1<=0){
return dp[S][v];
}
if(S==(1<>u&1){//下一步移动到顶点u
minn=min(minn,solve(S|1< 这种解法时间复杂度为O((2^n)*(n^2))
方法2:循环dp
状态压缩dp的一个难点是很难确定递推顺序。
所以一般的状态压缩题目都用记忆化搜索
这样比较的简洁
不过在这个问题中对于i,j如果他们对应集合满足S(i)⊆S(j),就有i≤j所以可以通过简洁的代码循环求解。
对于任一S⊆v,我们不能直接穷举它所代表的所有路径,然后求一个最小值,赋给d[vi][S],因为这样就变成了暴力法了。而动态规划的思想是,从S= Ø开始,求得A中包含一个元素时D的所有结果,A中包含两个元素时D的所有结果,一直到A包含了任一n-2个元素的所有d的结果。
为什么是n-2个呢? 对于d[vi][S]来说,当S包含vi本身的时候,对本题来说是没有意义的,比如,d[v2][{v2}]这个值,没有意义。
所以,当我们知道d[v2][{v3, v4, v5, v6}]的时候,我们也就知道了如果从v1出发,先到v2,所需要的最短回路是多少了。当我们求得了所有的d[vi][V - vi]时,本题就解出来了
伪代码如下:
#include
#include
using namespace std;
int n,INF=1e9;
int dp[1<<10001][10001],d[10001][10001];
int main(){
cin>>n;
for(int S=0;S<1<=0;S--){
for(int v=0;v>u&1)){
dp[S][v]=min(dp[S][v],dp[S|1< 这就是用dp解决TSP的思路。
像这样针对集合的dp我们一般叫做状压dp。。。