Codeforces Round #504 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final) ABCDE题解

第一次被hack祭

第一次掉rating祭

第一次rating在1500以下祭

正文开始：

A. Single Wildcard Pattern Matching

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two strings s

and t. The string s consists of lowercase Latin letters and at most one wildcard character '*', the string t consists only of lowercase Latin letters. The length of the string s equals n, the length of the string t equals m

.

The wildcard character '*' in the string s

(if any) can be replaced with an arbitrary sequence (possibly empty) of lowercase Latin letters. No other character of s can be replaced with anything. If it is possible to replace a wildcard character '*' in s to obtain a string t, then the string t matches the pattern s

.

For example, if s=

"aba*aba" then the following strings match it "abaaba", "abacaba" and "abazzzaba", but the following strings do not match: "ababa", "abcaaba", "codeforces", "aba1aba", "aba?aba".

If the given string t

matches the given string s

, print "YES", otherwise print "NO".

Input

The first line contains two integers n

and m (1≤n,m≤2⋅105) — the length of the string s and the length of the string t

, respectively.

The second line contains string s

of length n

, which consists of lowercase Latin letters and at most one wildcard character '*'.

The third line contains string t

of length m

, which consists only of lowercase Latin letters.

Output

Print "YES" (without quotes), if you can obtain the string t

from the string s

. Otherwise print "NO" (without quotes).

Examples

Input

Copy

6 10
code*s
codeforces

Output

Copy

YES

Input

Copy

6 5
vk*cup
vkcup

Output

Copy

YES

Input

Copy

1 1
v
k

Output

Copy

NO

Input

Copy

9 6
gfgf*gfgf
gfgfgf

Output

Copy

NO

Note

In the first example a wildcard character '*' can be replaced with a string "force". So the string s

after this replacement is "codeforces" and the answer is "YES".

In the second example a wildcard character '*' can be replaced with an empty string. So the string s

after this replacement is "vkcup" and the answer is "YES".

There is no wildcard character '*' in the third example and the strings "v" and "k" are different so the answer is "NO".

In the fourth example there is no such replacement of a wildcard character '*' that you can obtain the string t

so the answer is "NO".

什么垃圾玩意，通过人数还没有B和C多，一群hacked和FST的

先对第一个串从左到右扫一遍，如果没有*就直接比较两个字符串是否相等。如果有，就将第一个串拆成两部分，分别从前往后和从后往前比较即可。

#include
#include
#include
#include
#include
#include
#include
#include

B. Pair of Toys

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Tanechka is shopping in the toy shop. There are exactly n

toys in the shop for sale, the cost of the i-th toy is i burles. She wants to choose two toys in such a way that their total cost is k

burles. How many ways to do that does she have?

Each toy appears in the shop exactly once. Pairs (a,b)

and (b,a) are considered equal. Pairs (a,b), where a=b

, are not allowed.

Input

The first line of the input contains two integers n

, k (1≤n,k≤1014

) — the number of toys and the expected total cost of the pair of toys.

Output

Print the number of ways to choose the pair of toys satisfying the condition above. Print 0, if Tanechka can choose no pair of toys in such a way that their total cost is k

burles.

Examples

Input

Copy

8 5

Output

Copy

2

Input

Copy

8 15

Output

Copy

1

Input

Copy

7 20

Output

Copy

0

Input

Copy

1000000000000 1000000000001

Output

Copy

500000000000

Note

In the first example Tanechka can choose the pair of toys (1,4

) or the pair of toys (2,3

).

In the second example Tanechka can choose only the pair of toys (7,8

).

In the third example choosing any pair of toys will lead to the total cost less than 20

. So the answer is 0.

In the fourth example she can choose the following pairs: (1,1000000000000)

, (2,999999999999), (3,999999999998), ..., (500000000000,500000000001). The number of such pairs is exactly 500000000000.

感觉这题跟适合做A题啊QAQ

直接数（xia）学（gao）即可，注意特判

#include
#include
#include
#include
#include
#include
#include
#include

 

C. Bracket Subsequence

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A bracket sequence is a string containing only characters "(" and ")". A regular bracket sequence is a bracket sequence that can be transformed into a correct arithmetic expression by inserting characters "1" and "+" between the original characters of the sequence. For example, bracket sequences "()()" and "(())" are regular (the resulting expressions are: "(1)+(1)" and "((1+1)+1)"), and ")(", "(" and ")" are not.

Subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements.

You are given a regular bracket sequence s

and an integer number k. Your task is to find a regular bracket sequence of length exactly k such that it is also a subsequence of s

.

It is guaranteed that such sequence always exists.

Input

The first line contains two integers n

and k (2≤k≤n≤2⋅105, both n and k are even) — the length of s

and the length of the sequence you are asked to find.

The second line is a string s

— regular bracket sequence of length n

.

Output

Print a single string — a regular bracket sequence of length exactly k

such that it is also a subsequence of s

.

It is guaranteed that such sequence always exists.

Examples

Input

Copy

6 4
()(())

Output

Copy

()()

Input

Copy

8 8
(()(()))

Output

Copy

(()(()))

题目说了一大堆什么合法的算术表达式啊之类的，其实就是括号匹配啊。毕竟只有合法的括号匹配序列才会出现在合法的算术表达式内

#include
#include
#include
#include
#include
#include
#include
#include

 

D. Array Restoration

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Initially there was an array a

consisting of n integers. Positions in it are numbered from 1 to n

.

Exactly q

queries were performed on the array. During the i-th query some segment (li,ri) (1≤li≤ri≤n) was selected and values of elements on positions from li to ri inclusive got changed to i. The order of the queries couldn't be changed and all q queries were applied. It is also known that every position from 1 to n

got covered by at least one segment.

We could have offered you the problem about checking if some given array (consisting of n

integers with values from 1 to q

) can be obtained by the aforementioned queries. However, we decided that it will come too easy for you.

So the enhancement we introduced to it is the following. Some set of positions (possibly empty) in this array is selected and values of elements on these positions are set to 0

.

Your task is to check if this array can be obtained by the aforementioned queries. Also if it can be obtained then restore this array.

If there are multiple possible arrays then print any of them.

Input

The first line contains two integers n

and q (1≤n,q≤2⋅105

) — the number of elements of the array and the number of queries perfomed on it.

The second line contains n

integer numbers a1,a2,…,an (0≤ai≤q) — the resulting array. If element at some position j is equal to 0 then the value of element at this position can be any integer from 1 to q

.

Output

Print "YES" if the array a

can be obtained by performing q queries. Segments (li,ri) (1≤li≤ri≤n) are chosen separately for each query. Every position from 1 to n

should be covered by at least one segment.

Otherwise print "NO".

If some array can be obtained then print n

integers on the second line — the i-th number should be equal to the i-th element of the resulting array and should have value from 1 to q. This array should be obtainable by performing exactly q

queries.

If there are multiple possible arrays then print any of them.

Examples

Input

Copy

4 3
1 0 2 3

Output

Copy

YES
1 2 2 3

Input

Copy

3 10
10 10 10

Output

Copy

YES
10 10 10 

Input

Copy

5 6
6 5 6 2 2

Output

Copy

NO

Input

Copy

3 5
0 0 0

Output

Copy

YES
5 4 2

Note

In the first example you can also replace 0

with 1 but not with 3

.

In the second example it doesn't really matter what segments to choose until query 10

when the segment is (1,3)

.

The third example showcases the fact that the order of queries can't be changed, you can't firstly set (1,3)

to 6 and after that change (2,2) to 5. The segment of 5 should be applied before segment of 6

.

There is a lot of correct resulting arrays for the fourth example.

感觉自己做过把这题反过来的简单版本啊QAQ

先考虑没有0的情况，这时该如何判断给出的序列是否合法呢？

比如在n=3,q=3时，2 3 2 是合法的，而3 1 3 与1 2 1就是不合法的。

再多举几个例子不难发现这样的结论：对于任意一个首尾相同的序列，当这其中的最小值为序列的第一个元素时合法，反之则不然

我们便可以在预处理时记录下每个数字在序列中出现的位置（用vector存），然后从1到q进行枚举，当该数对应的vector非空时，取出其首尾元素作为起点与重点，判断该子序列的最小值是否为首元素所指向的原序列的值，这一步可以用st表或线段树实现

那么1 2 1为什么不合法呢？我们进行了三次操作，最后一次一定是将某些元素变成了3，然而1 2 1虽满足第一个条件，但是却没有出现绝对存在的操作数3，这提醒我们要进行一个特判：当序列中的最大值不为q时直接输出no

看起来已经解决一大半了是吧，我们再来考察有0的情况

0可以代表任意数，因此首先带来的一个问题是上面的特判不一定成立了，比如1 2 0，虽然没有出现3，但我们可以让0变成3从而这个序列就是合法的了。解决方法很简单，直接在特判上加一个有没有0的条件，有就让任意一个0变成q，没有则直接输出no

还要注意的是全0序列，它一定合法，但在输出时要将其全部作为最大值输出，这个也可以直接特判

接下来就大体类似了，注意，0在处理最小值时将0即为无穷大即可

对于合法序列的输出，非零数直接输出，若数为0则找到它右边的第一个非零数输出，否则就输出左边的

下面的程序是用st表实现的

#include
#include
#include
#include
#include
#include
#include
#include

E. Down or Right

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

This is an interactive problem.

Bob lives in a square grid of size n×n

, with rows numbered 1 through n from top to bottom, and columns numbered 1 through n from left to right. Every cell is either allowed or blocked, but you don't know the exact description of the grid. You are given only an integer n

.

Bob can move through allowed cells but only in some limited directions. When Bob is in an allowed cell in the grid, he can move down or right to an adjacent cell, if it is allowed.

You can ask at most 4⋅n

queries of form "? r1 c1 r2 c2" (1≤r1≤r2≤n, 1≤c1≤c2≤n). The answer will be "YES" if Bob can get from a cell (r1,c1) to a cell (r2,c2), and "NO" otherwise. In particular, if one of the two cells (or both) is a blocked cell then the answer is "NO" for sure. Since Bob doesn't like short trips, you can only ask queries with the manhattan distance between the two cells at least n−1, i.e. the following condition must be satisfied: (r2−r1)+(c2−c1)≥n−1

.

It's guaranteed that Bob can get from the top-left corner (1,1)

to the bottom-right corner (n,n) and your task is to find a way to do it. You should print the answer in form "! S" where S is a string of length 2⋅n−2 consisting of characters 'D' and 'R', denoting moves down and right respectively. The down move increases the first coordinate by 1, the right move increases the second coordinate by 1

. If there are multiple solutions, any of them will be accepted. You should terminate immediately after printing the solution.

Input

The only line of the input contains an integer n

(2≤n≤500

) — the size of the grid.

Output

When you are ready to print the answer, print a single line containing "! S" where where S

is a string of length 2⋅n−2 consisting of characters 'D' and 'R', denoting moves down and right respectively. The path should be a valid path going from the cell (1,1) to the cell (n,n)

passing only through allowed cells.

Interaction

You can ask at most 4⋅n

queries. To ask a query, print a line containing "? r1 c1 r2 c2" (1≤r1≤r2≤n, 1≤c1≤c2≤n). After that you should read a single line containing "YES" or "NO" depending on the answer of the query. "YES" means Bob can go from the cell (r1,c1) to the cell (r2,c2)

, "NO" means the opposite.

Note that the grid is fixed before the start of your solution and does not depend on your queries.

After printing a query do not forget to output end of line and flush the output. Otherwise you will get Idleness limit exceeded or other negative verdict. To do this, use:

• fflush(stdout) or cout.flush() in C++;
• System.out.flush() in Java;
• flush(output) in Pascal;
• stdout.flush() in Python;
• see documentation for other languages.

Answer "BAD" instead of "YES" or "NO" means that you made an invalid query. Exit immediately after receiving "BAD" and you will see Wrong answer verdict. Otherwise you can get an arbitrary verdict because your solution will continue to read from a closed stream.

Example

Input

Copy

4
 
YES
 
NO
 
YES
 
YES
 

Output

Copy

 
? 1 1 4 4
 
? 1 2 4 3
 
? 4 1 4 4
 
? 1 4 4 4
 
! RDRRDD

Note

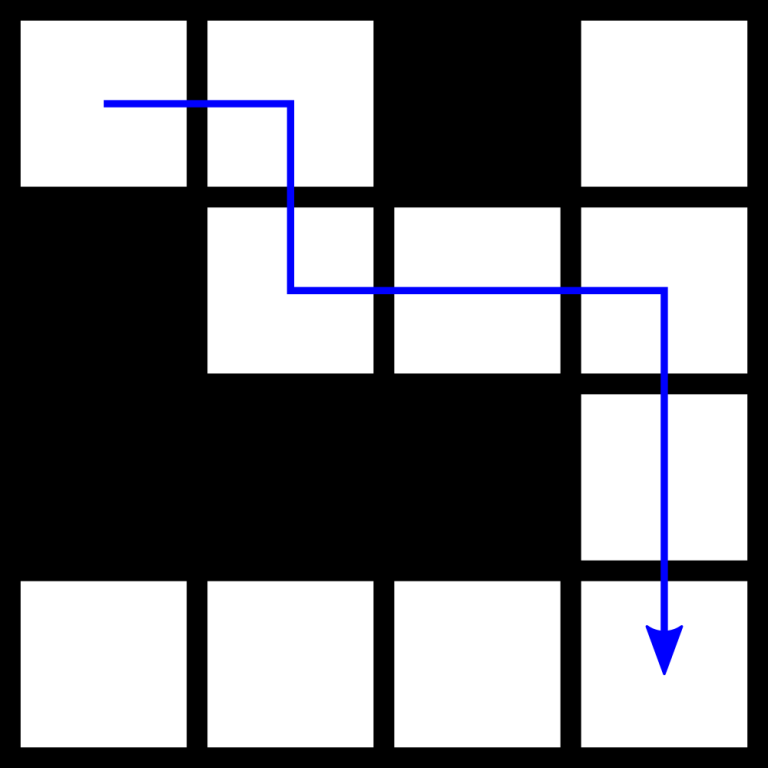
The first example is shown on the picture below.

To hack, use the following input format:

The first line should contain a single integer n

(2≤n≤500

) — the size of the grid.

Each of the next n

lines should contain a string of n

characters '#' or '.', where '#' denotes a blocked cell, and '.' denotes an allowed cell.

For example, the following text encodes the example shown above:

4
..#.
#...  
###.
....

交互题QAQ

把问题拆成两半来做

对于前半部分，记录当前位置为（x,y），直接询问（x+1，y）能否到达终点，如果能x++，否则y++;

那么后边部分呢？首先明确肯定和前半部分肯定不一样，因为其实的询问两点间距离会小于n-1，不符合题意

我们将当前走到的点记为（x,y）此时不能直接询问（x,y）能否到达（n,n）,但是我们知道在(x,y)之前的（x1,y1）是能到达的。那么有没有一种方法，能通过（x1,y1）来推出有新的点在答案路径上呢？

我们考虑与（n,n）相邻的点（n-1,n）如果（x1,y1）能到达（n-1.n）的话，又由于（x1,y1）能到达（n,n）,所以（n-1,n）一定能到达（n,n），那么（n-1,n）就可以记录在答案中了。而如果不能到达的话，由于保证有解，那么与（n,n）相邻的（n,n-1）一定是可行的。这样做，一边往前进，一边往后退，便可以完成后半部分的答案。

此题是VK cup 2018 Final的C题，不得不说还是有一定难度的，也许是不适应交互题的原因吧

#include
#include
#include
#include
#include
#include
#include
#include