考研错题本——计算机组成原理（数据的表示和运算）

2 数据的表示和运算

2.1 数制与编码

【习题】

【解析】（10100101）不是合法的8421码， 因为在8421码中，1010~1111是不能使用的

【回顾】

【习题】

【解析】B，两个8421码相加之和大于等于1010时，要加修正，计算机是这么做的，但是我们先将二进制转成十进制计算完之后再转回二进制

【习题】

【解析】
I 错误，大于等于2；III 错误，仅靠增加就校验位的位数，是不能提高正确性的，还要考虑码距；IV 错误，采用奇偶检验可检测出一位数据错误的位置，但是不能给出纠正；其余均正确

【回顾】

【习题】

【解析】一位就检验码只能发现奇数位错误，无法发现偶数位错误
【回顾】


【习题】

【解析】D

【习题】

【解析】 C
【回顾】

【习题】

【解析】

【回顾 - 海明码】

2.2 定点数的表示与运算

【原码、补码、反码、译码的转换】

【0 的表示】



【算术移位】

都不动符号位

【求 -x 的补码】

【补码的优点】

【关于数据类型转换的总结】

• 由于 signed 转化为等长的 unsigned 时，符号位成为数据的一部分
• long 类型转化为 short 类型，只将低 16 位传过去
• 短字长整数到长字长整数的转换，高位部分扩展为原数字的符号位
• char 类型为 8 位 ASCII 码整数，其转换为 int 时，在高位部分补 0 即可

【原码一位乘】


【补码一位乘（booth）】



【乘法运算总结】

【原码不回复余数除法】



【补码不恢复余数除法】



【除法运算总结】

【习题】

【解析】C语言的数据在内存中为补码形式，x = 0000007FH， y = FFF7H，强行转换为 int 之后为 FFFFFFF7H， x+y = 0000007FH+FFFFFFF7H

【习题】

【解析】B，$r1=-2，r2=-14，r3=-112，r4=-8$，8 位补码所能表示的补码范围为 -128~127

【回顾——表示范围】

下面的所有讨论，机器字长都为 $n+1$

由于 0 的原码和反码都有两种，补码只有唯一一种，所以对于定点整数补码可以比原码和反码多表示一个负数，即首位是 1 后面全是 0， 即 $-2^n$

对于定点小数补码可以比原码和反码多表示一个数，即 -1

【习题】

【解析】考虑到小端和字节对齐的问题， int 占 4 字节，char占 1 字节，short 占 2字节

【回顾】

大端方式按照从最高有效字节到最低有效字节的顺序存储数据
小端方式按照从最低有效字节到最高有效字节的顺序存储数据

下面以一个图说明字节对齐的问题

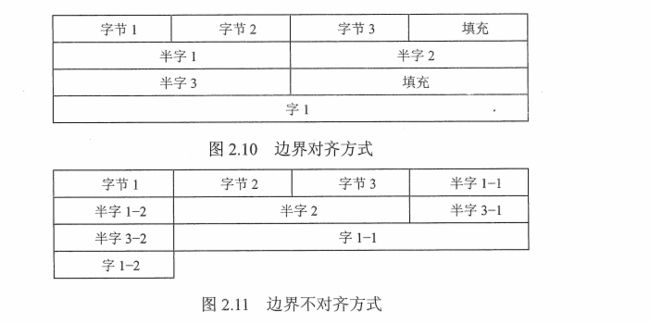
【习题】

【解析】B

【习题】

【解析】D

【习题】

【解析】A

【习题】

【解析】D

5 位二进制定点小数，用补码表示时，最小负数表示为 1.0000，其真值为 -1

【习题】

【解析】B

【回顾】

【习题】

【解析】D

【习题】
【解析】C，取特值，$[-8{]}_{补}=1,111000$，再取 $[-32{]}_{补}=1,100000$

【习题】

【解析】C，取特值， $[-32{]}_{补}=1,00000$ ，这个是特殊的补码，刚好是比原码、反码多出来的那一个负数

【习题】

【解析】C，取$[-1{]}_{补}=1.000$，再取 $[-0.625{]}_{补}=1.011$

【习题】

【解析】C

【回顾】

【习题】

【解析】D

【习题】

【解析】C

【习题】

【解析】D

【习题】

【解析】B

【习题】

【解析】D

【习题】

【解析】B
【回顾】


【习题】

【解析】C

【习题】

【解析】B

【习题】

【解析】B
【回顾】


【习题】

【解析】D
【回顾】


【习题】

【解析】B

【习题】

【解析】D

【习题】

【解析】D

【习题】

【解析】B
【回顾】



【习题】

【解析】D

【习题】

【解析】B，是补码，转换成原码需要减一再取反，所以正确答案是 $10000011$

【习题】

【解析】A，double 占 8 字节

【习题】

【解析】A，还是没有考虑字节的问题，C0 是一个字节

【习题】

【解析】B
【回顾】

【习题】

【解析】A

【习题】

【解析】

【习题】


【解析】

【习题】

【解析】

【回顾】

【习题】

【解析】

【回顾】

【习题】


【解析】

2.3 浮点数的表示和运算

【规格化的作用】

【如何判断一个浮点数是否是规格化数】

【浮点数表示范围】

【习题】

【解析】C

【习题】

【解析】D

【习题】

【解析】

【补充】

【习题】

【解析】

【习题】

【解析】

【回顾】

【习题】

【解析】D

【回顾】


【习题】

【解析】B

【习题】

【解析】A

【习题】

【解析】A
【习题】

【解析】D
尾数 8 位，补码，能表示的范围为 $-1～1-2^{-7}$；阶码 4 位，补码能表示的最大整数为 $2^{4-1}-1=7$，故该浮点数所能表示的最大正数为 $(1-2^{-7})\times 2^7$

【习题】

【解析】B

【习题】

【解析】B

【习题】

【解析】C
【回顾】

【习题】

【解析】B
【回顾】

【习题】

【解析】C

【习题】

【解析】A

【习题】

【解析】A

【习题】

【解析】D

【习题】

【解析】D

【习题】

【解析】A

【回顾】

【习题】

【解析】B

【习题】

【解析】D

【习题】

【解析】C

【习题】

【解析】D

【习题】

【解析】

【习题】

【解析】

【习题】

【解析】


【习题】

【解析】

【习题】

【解析】

【习题】

【解析】

【回顾】

因为阶码表示范围是$1-254$，减去偏移量 $127$ 就是 $-126$ 到 $127$。当阶码全为 $0$ 或 全为 $1$ （即 $255$）时有特殊用途。阶码为 $0$，表示浮回点数为 $0$ 值；阶码为$255$，若尾数全 $0$，表示无穷大，否则表示无效数字。根据符号位，可以分为正负无穷和正负 $0$

【习题】

【解析】

2.4 算术逻辑单元

【串行进位、并行进位的逻辑表达式】

【习题】

【解析】B

【习题】

【解析】B
每片74181是4位的内部先行进位的ALU芯片（组内并行、组间串行），每4片74181与1片74182相连，可组成一个两级先行进位结构的16位ALU，两个这种结构的16位ALU串行进位构成两级先行进位的32位ALU

【习题】

【解析】D