数据结构_实验三_二叉树的基本操作

1.需求分析

1.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。
输入输出形式：

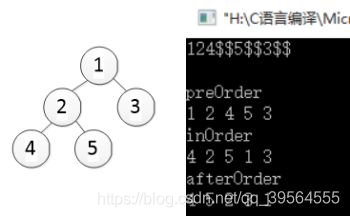
124$$5$3$$

preOrder
1 2 4 5 3
inOrder
4 2 5 1 3
afterOrder
4 5 2 3 1

功能：利用树存储数据，采用递归的方式做到先序、中序、后序三种遍历方式输出
数据范围：0~9
测试数据：

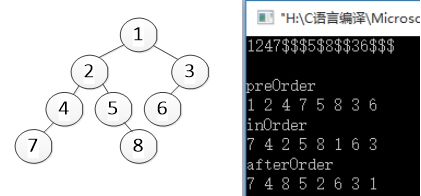
124$$5$3$$                             1247$$$5$8$$36$$$

1.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。
输入输出形式：

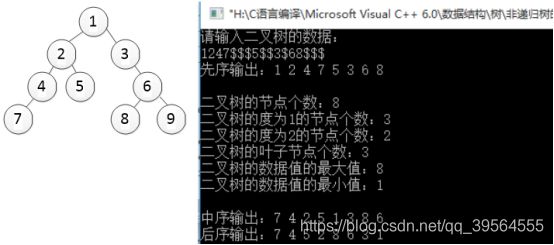
 124$$56$$$3$$

先序输出：1 2 4 5 6 3

二叉树的节点个数：6
二叉树的度为1的节点个数：1
二叉树的度为2的节点分数：2
二叉树的叶子节点个数：3
二叉树的数据值的最大值：6
二叉树的数据值的最小值：1

中序输出：4 2 6 5 1 3

后序输出：4 6 5 2 3 1
功能：利用树存储数据，采用非递归的方式做到先序、中序、后序三种遍历方式输出
数据范围：0~9
测试数据：

124$$56$$$3$$                         1247$$$5$$3$68$$$

2.概要设计

2.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。
  创建二叉树时，利用递归思想，先输入根节点，再输入左子树，再该节点的左子树，直到此节点没有左子树，没有该节点则输入$，然后输入右子树，直到输入第一个左子树，再输入根节点的右子树，接下来的输入即雷同把该节点当根节点的输入。

2.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。
  节点统计即输出数据个数；度为1的节点为只有左子树或右子树的节点；度为2的节点为有左子树和右子树的节点；叶子节点即没有左子树和右子树的节点；最大值和最小值循环对比。

3.详细设计

3.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。
  创建二叉树的函数：
  输入一连串数据；
  单个读取
  if（$）
    该结点为零
  else
     将数据赋值给该节点
    调用创建二叉树函数输入该节点的左子树
    调用创建二叉树函数输入该节点的右子树
  返回创建的二叉树

先序输出的函数：
接受二叉树
从根节点开始读取单个节点
if（该节点的数据不是$）
  输出该节点的数据
  调用先序输出函数输出该节点的左子树
  调用先序输出函数输出该节点的右子树

中序输出的函数：
接收二叉树
从根节点开始读取单个节点
if（该节点的数据不是$）
  调用中序输出函数输出该节点的左子树
  输出该节点的数据
  调用中序输出函数输出该节点的右子树
后序输出的函数：
接收二叉树
从根节点开始读取单个节点
if（该节点的数据不是$）
  调用后序输出函数输出该节点的左子树
  调用后序输出函数输出该节点的右子树
  输出该节点的数据

3.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。
  计算节点即为简单的if语句然后自加，最大值和最小值循环对比取值。

4.用户使用说明

4.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。
  用户先画一个二叉树，再从根节点开始输入，对于该节点先左子树后右子树，若该处为空，则输入$。

4.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。
  输入同5.1

5.测试结果

5.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。
输入数据：

124$$5$3$$

输入数据：

1247$$$5$8$$36$$$

5.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。
输入数据：

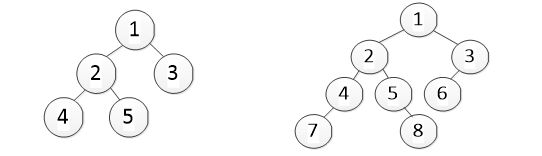
124$$56$$$3$$

输入数据：

1247$$$5$$3$68$$$

6.附录
6.1 输入数据建立二叉树，分别以前序、中序、后序的遍历方式显示输出二叉树的遍历结果。

#include 
using namespace std;

typedef struct tTree{
    char date;
    struct tTree * rTree;
    struct tTree * lTree;
}tTree;

tTree * creatBiTree(tTree *T)    //创建二叉树
{
    char num;

    cin>>num;
    if(num=='$')   //输入$终止
        T=NULL;
    else
    {
        T = new tTree;
        T->date=num;
        T->lTree = creatBiTree(T->lTree);   //递归输入左孩子
        T->rTree = creatBiTree(T->rTree);   //递归输入右孩子
    }

    return T;
}

void preOrder(tTree * T)     //先序输出二叉树
{
    if(T!=NULL)
    {
        cout<<T->date<<" ";
        preOrder(T->lTree);
        preOrder(T->rTree);
    }
}

void inOrder(tTree * T)    //中序输出二叉树
{
    if(T!=NULL)
    {
        inOrder(T->lTree);
        cout<<T->date<<" ";
        inOrder(T->rTree);
    }
}

void afterOrder(tTree * T)   //后序输出二叉树
{
    if(T!=NULL)
    {
        afterOrder(T->lTree);
        afterOrder(T->rTree);
        cout<<T->date<<" ";
    }
}

int main()
{
    tTree * T;
    T=creatBiTree(T);
    cout<<endl<<"preOrder"<<endl;   //先序输出
    preOrder(T);
    cout<<endl<<"inOrder"<<endl;    //中序输出
    inOrder(T);
    cout<<endl<<"afterOrder"<<endl; //后序输出
    afterOrder(T);
    cout <<endl;

    return 0;
}

6.2 采用非递归的编程方法，分别统计二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值。

#include 
using namespace std;

/*采用非递归的编程方法，分别统计
二叉树的节点个数、度为1、度为2和叶子节点的个数，
以及数据值的最大值和最小值
*/

typedef struct tTree{
    char date;
    struct tTree * lchild;
    struct tTree * rchild;
}tTree;

tTree * createBiTree(tTree * Tree)    //创建二叉树
{
    char num;

    cin>>num;
    if(num=='$')
        Tree=NULL;
    else
    {
        Tree = new tTree;
        Tree->date=num;
        Tree->lchild=createBiTree(Tree->lchild);
        Tree->rchild=createBiTree(Tree->rchild);
    }
    return Tree;
}

void preOrder(tTree * Tree)   //非递归先序输出二叉树
{
    tTree *p;
    tTree *stack[100];
    int top = 0;
    p=Tree;

    //二叉树的节点个数、度为1、度为2和叶子节点的个数，以及数据值的最大值和最小值
    int numOfNode, numOfOneDu, numOfTwoDu, numOfLeaves;
    numOfNode = numOfOneDu = numOfTwoDu = numOfLeaves = 0;
    char numOfMax, numOfMin;
    numOfMax = numOfMin = p->date;

    while(p || top!=0)
    {
        while(p)    //遍历左子树
        {
            cout<<p->date<<" ";
            //统计比较
            numOfNode++;       //统计节点个数
            if((p->lchild!=NULL&&p->rchild==NULL)|| (p->lchild==NULL&&p->rchild!=NULL) )   //统计度为1的节点
                numOfOneDu++;
            if(p->lchild!=NULL&&p->rchild!=NULL)  //统计度为2的节点
                numOfTwoDu++;
            if(p->lchild==NULL&&p->rchild==NULL)   //统计叶子节点
                numOfLeaves++;
            if( numOfMax < (p->date) )         //比较得到最大值
                numOfMax = p->date;
            if( numOfMin > (p->date) )         //比较得到最小值
                numOfMin = p->date;

            if(p->rchild)
            {
                stack[top++] = p->rchild;
            }
            p=p->lchild;
        }//endwhile
        if(top!=0)
        {
            p = stack[--top];
        }//endif
    }//end of while
    cout<<endl<<endl;
    cout<<"二叉树的节点个数："<<numOfNode<<endl;
    cout<<"二叉树的度为1的节点个数："<<numOfOneDu<<endl;
    cout<<"二叉树的度为2的节点个数："<<numOfTwoDu<<endl;
    cout<<"二叉树的叶子节点个数："<<numOfLeaves<<endl;
    cout<<"二叉树的数据值的最大值："<<numOfMax<<endl;
    cout<<"二叉树的数据值的最小值："<<numOfMin<<endl;
}

void inOrder(tTree *Tree)  //非递归中序输出
{
    tTree *p;
    tTree *stack[100];
    p=Tree;
    int top =0;
    while( p || top!=0 )
    {
        while(p)
        {
           stack[top++]=p;
            p=p->lchild;
        }
        p=stack[--top];
        cout<<p->date<<" ";
        p=p->rchild;
    }
}

void afterOrder(tTree *Tree)  //非递归后序输出
{
    tTree *p;
    tTree *stack[100];
    int status[100];
    int top = 0;
    int tempstatus;
    p=Tree;
    if(p)
    {
        stack[top] = p;
        status[top]=1;
        top++;
    }
    while(top!=0)
    {
        top = top - 1;
        p= stack[top];
        tempstatus = status[top];
        switch(tempstatus)
        {
            case 1:{       //根节点处理
                stack[top] = p;
                status[top] = 2;
                top++;
                if(p->lchild)
                {
                    stack[top] = p->lchild;
                    status[top] = 1;
                    top++;
                }
            }
            break;
            case 2:{
                stack[top] = p;
                status[top] = 3;
                top++;
                if(p->rchild)
                {
                    stack[top] = p->rchild;
                    status[top] = 1;
                    top++;
                }
                break;
            }
            case 3:{
                cout<<p->date<<" ";
                break;
            }
        }//end of switch
    }//endwhile
}

int main()
{
    cout<<"请输入二叉树的数据："<<endl;
    tTree *head = createBiTree(head);
    cout<<"先序输出：";
    preOrder(head);
    cout<<endl<<"中序输出：";
    inOrder(head);
    cout<<endl<<"后序输出：";
    afterOrder(head);
    cout<<endl;

    return 0;
}