蓝桥杯算法训练(java)--网络流裸题
题目:一个有向图,求1到N的最大流
输入格式
第一行N M,表示点数与边数
接下来M行每行s t c表示一条从s到t的容量为c的边
先备知识与注意事项
考虑如下情境:
在某个污水处理厂的某一道程序里,有一个「进水孔」,和一个「排水孔」,中间由许多「孔径不一」的水管连接起来,因为水管的「孔径大小」会影响到「每单位时间的流量」,因此要解决的问题,就是找到每单位时间可以排放「最大流量( flow )」的「排水方法」。
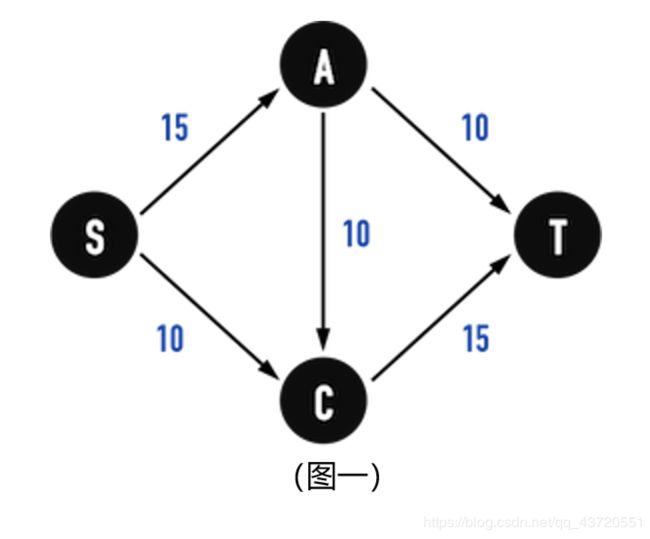
以图一为例,进水孔为vertex(S),排水孔为vertex(T),中间要经过污水处理站vertex(A)与vertex(C)边(edge)代表水管,边的权重(weight)(以下将称为capacity )表示水管的「孔径」。
考虑两种「排水方法」的flow:
- 第一种「分配水流」的方法,每单位时间总流量为20:
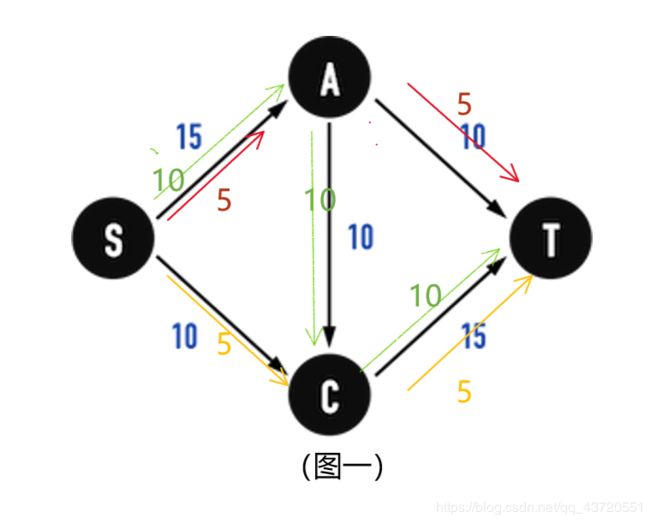
在Path : S− A − T上每单位时间流了5单位的水;
在Path : S− A − C− T上每单位时间流了10单位的水(问题出在这,占去了edge(C,T)的容量);
在Path : S− C− T上,因为edge(C,T)上只剩下「5单位的容量」,因此每单位时间流了5单位的水。 - 第二种「分配水流」的方法,每单位时间总流量为25:

在Path : S− A − T上每单位时间流了10单位的水;
在Path : S− A − C− T上每单位时间流了5单位的水;
在Path : S− C− T上,因为edge(C,T)上刚好还有「10单位的容量」,因此每单位时间流了10单位的水;
从以上两种「排水方式」可以看得出来,解决问题的精神,就是如何有效利用水管的「孔径容量」,让最多的水可以从「进水孔」流到「排水孔」。这就是在网络流(Flow Networks)上找到最大流量(Maximum Flow )的问题。
以下将介绍Ford-Fulkerson Algorithm (若使用BFS搜寻路径,又称为Edmonds-Karp Algorithm )来解决这个问题。
目录
一、Flow Networks基本性质
二、Ford-Fulkerson Algorithm
- Residual Networks(剩余网路)
- Augmenting Paths(增广路径)
- 演算法概念
- 代码
一、 网络流(Flow Networks)基本性质
Flow Networks是一个带权有向图,其edge(X,Y)具有非负的capacity,c(X,Y)≥0,如图二(a)。我们可以利用一个矩阵存储图信息。
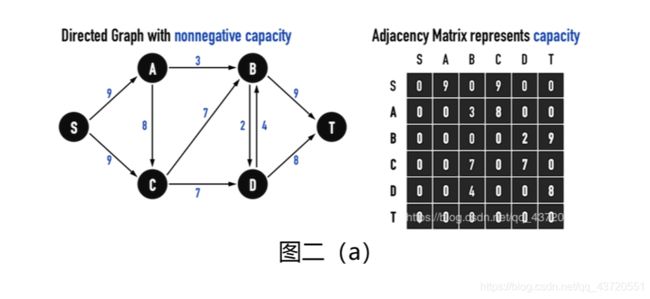
(此处以capacity取代权重,capacity就是「水管孔径」。)
-
若不存在edge(X,Y),則定义c(X,Y)=0。
-
特別地,要区分两个vertex:
source:表示Flow Networks的「流量源头」,以s表示;
sink:表示Flow Networks的「流量终点」,也称termination,以t表示。
- Capacity constraint: f ( X , Y ) ≤ c ( X , Y ) f( X, Y) ≤ c ( X, Y) f(X,Y)≤c(X,Y)
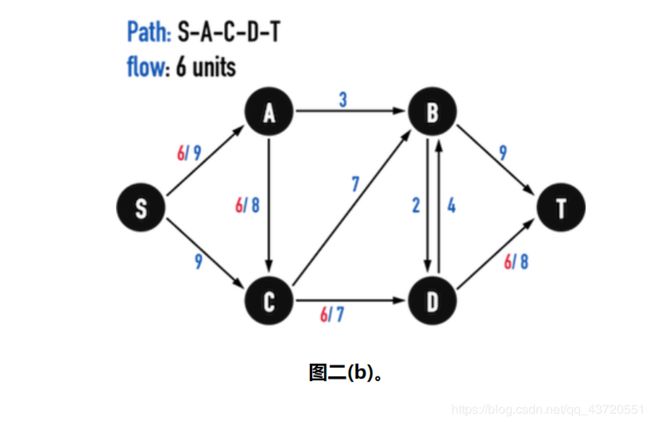
从vertex(X)流向vertex(Y)的flow,不能比edge(X,Y)的capacity还大.以图二(b)为例,在Pa t h : S− A − C− D − T上的edge之capacity皆大于6,因此在此路径上流入6单位的flow是可行的。最小的f(X,Y)=7,所以流过的flow只要小于等于7即可。 - Skew symmetry: f ( X , Y ) = − f ( Y , X ) f(X,Y)=-f(Y,X) f(X,Y)=−f(Y,X)
若定义「从vertex(X)指向vertex(Y)」之edge(X,Y)上,有5单位的flow,f( X, Y) = 5,这就等价于,从vertex(Y)到vertex(X)之edge(Y,X)上,有−5单位的flow,f( Y, X) = − 5。与「电子流(负电荷)」与「电流(正电荷)」的概念雷同, - Flow conservation:对Graph中除了source与sink以外的vertex(X)而言,所有「流进flow」之总和要等于所有「流出flow」的总和。也就是水流不会无故增加或无故减少,可视为一种能量守恒。
二、Ford-Fulkerson Algorithm
Ford-Fulkerson Algorithm需要两个辅助工具:
- Residual Networks (剩余网路,残差图)
- Augmenting Paths (增广路径)
1.Residual Networks(剩余网路)
Residual Networks的概念为,记录Graph上之edge还有多少「剩余的容量」可以让flow流过。

以图三(a)为例。
- 若在Pa t h : S− A − C− D − T上的所有edge都有6单位的flow流过,那么这些edge(edge(S,A)、edge(A,C)、edge(C,D)、edge(D,T))的可用「剩余capacity」,都应该要「减6」,例如,edge(S,A)只能「再容纳9−6=3单位」的flow,edge(C,D)只能「再容纳7−6=1单位」的flow。
- 最关键的是,若「从vertex(A)指向vertex(C )」之edge(A,C)上,有6单位的flow流过, f ( A , C ) = 6 f( A , C) = 6 f(A,C)=6,那么在其Residual Networks上,会因应产生出一条「从vertex(C ) 指向vertex(A)」的edge(C,A),并具有6单位的residual capacity, c f ( C , A ) = 6 。 cf( C, A ) = 6。 cf(C,A)=6。 (证明见下)
这些「剩余capacity」就称为residual capacity,以 c f cf cf表示。 edge之capacity以residual capacity取代,见图三(a)右。
数学证明:
因为Skew symmetry, f ( C , A ) = − f ( A , C ) f( C, A ) = − f( A , C) f(C,A)=−f(A,C);
再根据定义, c f ( C , A ) = c ( C , A ) − f ( C , A ) = c ( C , A ) + f ( A , C ) = 0 + 6 = 6 , cf( C, A ) = c ( C, A ) − f( C, A ) = c ( C, A ) + f( A , C) = 0 + 6 = 6, cf(C,A)=c(C,A)−f(C,A)=c(C,A)+f(A,C)=0+6=6,
其物理意义呢?可以用「如果想要重新配置水流方向」来理解。

根据图(b1),我们可以将其看成是,我们已经有了一个通过6个单位的流量的剩余网络(图(a)右)上,如果现在想经过Path : S− C− A − B − T流过2单位的flow。
根据图(b1)画出的残差图为图(b2)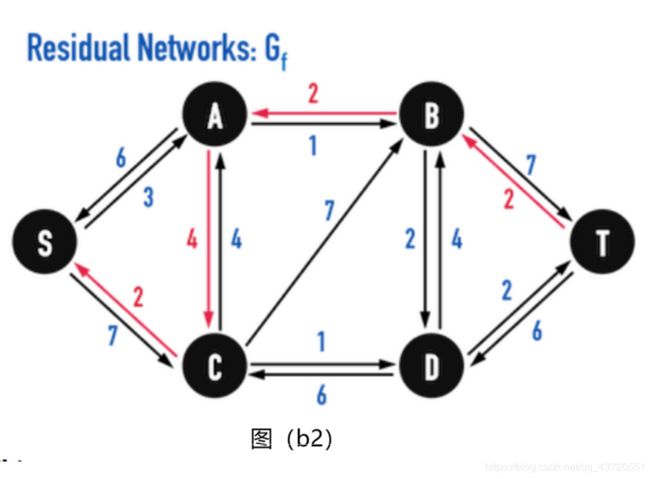
上面的图还可以看成是什么的残差图呢?
还可以看成是图(b3)的残差图。
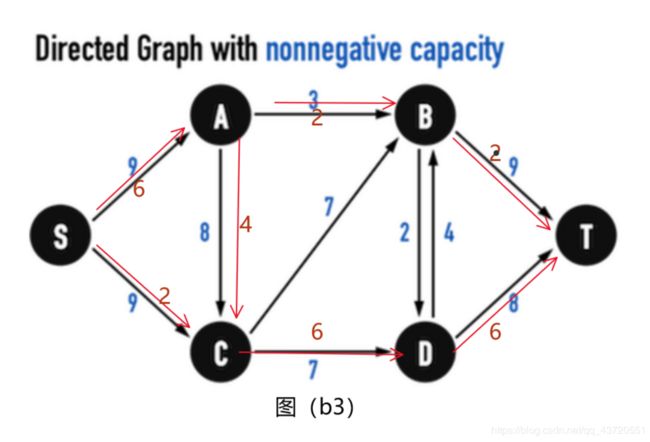
即在原图上直接流过上述红线的路径。这个和上图的区别在于
在图三(a)已经有6单位的flow从vertex(A)流向vertex( C ),现在可以从edge(A,C)上把2单位的flow「收回」,转而分配到edge(A,B)上,而edge(A,C)上,就剩下4单位的flow,最后的结果如图三(b3)所示。
我们根据图三(b3)可以看出流入sink (或称termination )的flow累加到8单位。
综上:若edge(X,Y)上有flow流过,f( X, Y),便将edge(X,Y)上的residual capacity定义为:
c f ( X , Y ) = c ( X , Y ) − f ( X , Y ) cf( X, Y) = c ( X, Y) − f( X, Y) cf(X,Y)=c(X,Y)−f(X,Y)
c ( X , Y ) c ( X, Y) c(X,Y)为原来水管孔径大小;
f ( X , Y ) f( X, Y) f(X,Y)表示目前水管已经有多少流量;
c f ( X , Y ) cf( X, Y) cf(X,Y)表示水管还能再容纳多少流量。
2. Augmenting Paths(增广路径)
在Residual Networks里,所有能够「从source走到termination」的路径,也就是所有能够「增加flow的path」,就称为Augmenting Paths。
3.演算法
Ford-Fulkerson Algorithm (若使用BFS搜寻路径,又称为Edmonds-Karp Algorithm)的方法如下:
-
在Residual Networks上寻找Augmenting Paths。
若以BFS()寻找,便能确保每次找到的Augmenting Paths一定经过「最少的edge」。(对于所有边长度相同的情况,比如地图的模型,bfs第一次遇到目标点,此时就一定是从根节点到目标节点最短的路径(因为每一次所有点都是向外扩张一步,你先遇到,那你就一定最短)。bfs先找到的一定是最短的) -
找到Augmenting Paths上的「最小residual capacity」加入总flow。
再以「最小residual capacity」更新Residual Networks上的edge之residual capacity。 -
重复上述步骤,直到再也没有Augmenting Paths为止。
便能找到Maximum Flow。
例子:
step1. 先以「flow=0」对residual networks進行初始化,如图五(a)。
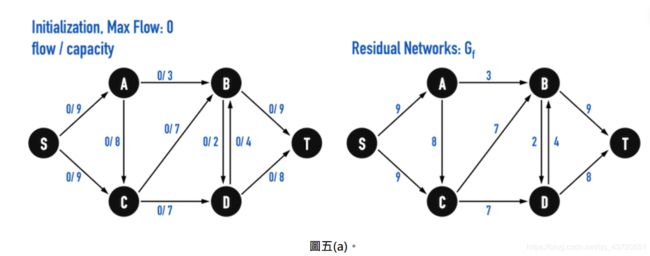
step2. 在Residual Networks上寻找Augmenting Paths。
在G f上,以BFS()找到能够从vertex(S)走到vertex(T),且「egde数最少」的路径:Pa t h : S− A − B − T,见图五(b)。
BFS()有可能找到都是3条edge的Pa t h : S− A − B − T或是Pa t h : S− C− D − T。这里以前者为例。
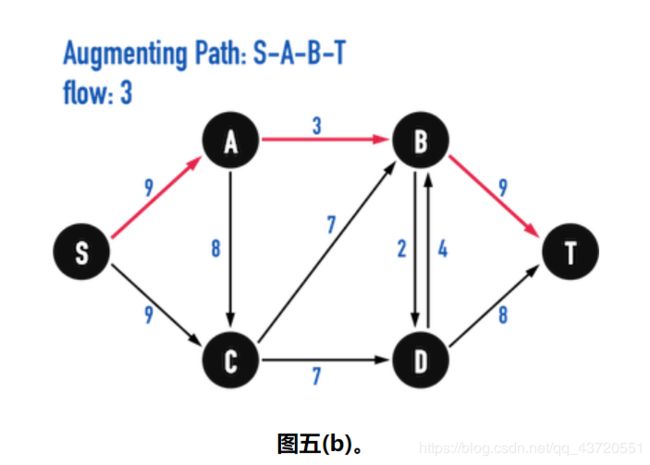
step3. 找到Augmenting Paths上的「最小residual capacity」加入总flow。
「最小residual capacity」=3
f l o w = f l o w + 3 flow=flow+3 flow=flow+3
step4. 以「最小residual capacity」更新Residual Networks上的edge之residual capacity
c f ( S , A ) = c ( S , A ) − f ( S , A ) = 9 − 3 = 6 cf(S,A)=c(S,A)−f(S,A)=9−3=6 cf(S,A)=c(S,A)−f(S,A)=9−3=6
c f ( A , S ) = c ( A , S ) − f ( A , S ) = 0 + 3 = 3 cf(A,S)=c(A,S)−f(A,S)=0+3=3 cf(A,S)=c(A,S)−f(A,S)=0+3=3
c f ( A , B ) = c ( A , B ) − f ( A , B ) = 3 − 3 = 0 cf(A,B)=c(A,B)−f(A,B)=3−3=0 cf(A,B)=c(A,B)−f(A,B)=3−3=0
c f ( B , A ) = c ( B , A ) − f ( B , A ) = 0 + 3 = 3 cf(B,A)=c(B,A)−f(B,A)=0+3=3 cf(B,A)=c(B,A)−f(B,A)=0+3=3
c f ( B , T ) = c ( B , T ) − f ( B , T ) = 9 − 3 = 6 cf(B,T)=c(B,T)−f(B,T)=9−3=6 cf(B,T)=c(B,T)−f(B,T)=9−3=6
c f ( T , B ) = c ( T , B ) − f ( T , B ) = 0 + 3 = 3 cf(T,B)=c(T,B)−f(T,B)=0+3=3 cf(T,B)=c(T,B)−f(T,B)=0+3=3
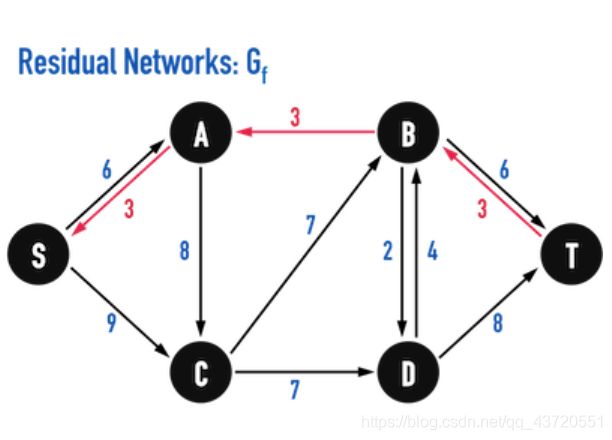
重复上述操作,对上述残差图继续寻找增广路径,直到找不到增广路径为止。
4. 代码
- 使用AdjMatrix建立Graph,並利用AdjMatrix[X][Y]存edge(X,Y)的weight。
private static void buildGragh(int[][] gragh, int vertex1, int vertex2, int weight) {
gragh[vertex1][vertex2] += weight;// 一条边可能会出现多次
}
- BFSfindExistingPath():利用Breadth-First Search寻找「从source走到termination」的路徑,而且是edge数最少的路径。
private static boolean BFSfindPath(int[][] gragh, int s, int t, int[] path) {
// path[]是通过记录每个结点的父节点,从而记录下一条完整的路径。
for (int i = 0; i < path.length; i++) {
path[i] = 0;
}
int vertex_num = gragh.length;
// 用于标记是否已经访问过该结点,默认是没有访问过的
boolean[] visited = new boolean[vertex_num];
Queue<Integer> q = new ArrayDeque<Integer>();
q.add(s);
visited[s] = true;
while (q.isEmpty() == false) {
int tem = q.poll();
for (int i = 1; i < vertex_num; i++) {
if (gragh[tem][i] > 0 && visited[i] == false) {
q.add(i);
visited[i] = true;
path[i] = tem;
}
}
}
return visited[t] == true;
}
- MinCapacity():用来找到从BFSfindExistingPath()找到的路劲上,最小的residual capacity。
private static int minCapacity(int[] path, int[][] gragh) {
int min = gragh[path[path.length - 1]][path.length - 1];
for (int i = path.length - 2; i != 1; i = path[i]) {
if (gragh[path[i]][i] < min && gragh[path[i]][i] > 0) {
//如果不是>0则可能把没有边的也算进去。
min = gragh[path[i]][i];
}
}
return min;
}
4.演算法思路
int flow = 0;
while (BFSfindPath(gragh, 1, n, path)) {
// 如果能够找到增广路径,那么我们在该路径上能够通过的容量就是这个路径上能通过的最小容量。
int min_capacity = minCapacity(path, gragh);
flow += min_capacity;
for (int i = n; i != 1; i = path[i]) {
int j = path[i];
gragh[j][i] -= min_capacity;
gragh[i][j] += min_capacity;
}
}
总体代码如下:
//参考链接https://alrightchiu.github.io/SecondRound/flow-networksmaximum-flow-ford-fulkerson-algorithm.html
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.Scanner;
public class Maximum {
public static void main(String[] args) {
Scanner scn = new Scanner(System.in);
// 输入结点个数和边的个数
int n = scn.nextInt();
int m = scn.nextInt();
// 因为第一个结点时1不是0,所以我们多申请一些空间,索引为0的位置就不使用了。从索引为1的位置看是放
// gragh[i][j]是第i个结点到第j个结点的权重。
int[][] gragh = new int[n + 1][n + 1];
for (int i = 0; i < m; i++) {
int vertex1 = scn.nextInt();
int vertex2 = scn.nextInt();
int weight = scn.nextInt();
buildGragh(gragh, vertex1, vertex2, weight);
}
// path[i]是第i个结点的父节点。我们通过在BFS中不断更新path[i]里的数,从而保存一条路径。
int[] path = new int[n + 1];
int flow = 0;
while (BFSfindPath(gragh, 1, n, path)) {
// 如果能够找到增广路径,那么我们在该路径上能够通过的容量就是这个路径上能通过的最小容量。
int min_capacity = minCapacity(path, gragh);
flow += min_capacity;
for (int i = n; i != 1; i = path[i]) {
int j = path[i];
gragh[j][i] -= min_capacity;
gragh[i][j] += min_capacity;
}
}
System.out.println(flow);
}
private static void buildGragh(int[][] gragh, int vertex1, int vertex2, int weight) {
gragh[vertex1][vertex2] += weight;// 一条边可能会出现多次
}
private static boolean BFSfindPath(int[][] gragh, int s, int t, int[] path) {
// path[]是通过记录每个结点的父节点,从而记录下一条完整的路径。
for (int i = 0; i < path.length; i++) {
path[i] = 0;
}
int vertex_num = gragh.length;
// 用于标记是否已经访问过该结点,默认是没有访问过的
boolean[] visited = new boolean[vertex_num];
Queue<Integer> q = new ArrayDeque<Integer>();
q.add(s);
visited[s] = true;
while (q.isEmpty() == false) {
int tem = q.poll();
for (int i = 1; i < vertex_num; i++) {
if (gragh[tem][i] > 0 && visited[i] == false) {
q.add(i);
visited[i] = true;
path[i] = tem;
}
}
}
return visited[t] == true;
}
private static int minCapacity(int[] path, int[][] gragh) {
int min = gragh[path[path.length - 1]][path.length - 1];
for (int i = path.length - 2; i != 1; i = path[i]) {
if (gragh[path[i]][i] < min && gragh[path[i]][i] > 0) {
min = gragh[path[i]][i];
}
}
return min;
}
}
上述代码在蓝桥杯提交里有一组数据无法通过。我怀疑是该数据错误!!
我将数据下载下来看,发现它给的是一个100个结点,10000条边的图。按理说应该要有接下来要有10000 行数表示边的信息,但是只有1000行,这样运行时,程序会一直等待接下来的9000行,这就会导致运行错误,而当我把数据进行修改,将10000改成1000,代码能够运行,并且答案和官网给的答案是一致的。