详解2020 CCPC-Wannafly Winter Camp Day3 Div.1 G火山哥周游世界 树dp

题目链接
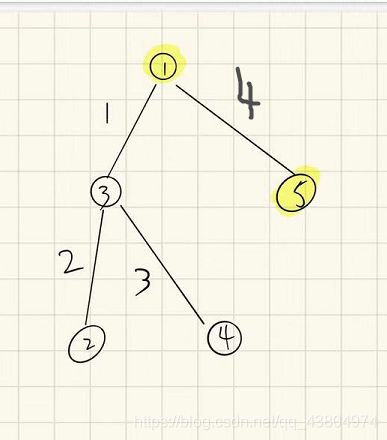上面是样例2的图，首先我们看到数据范围就一定要明确，肯定不是暴力，然后由于题目说了是n个点n-1条边，这就是一棵树，在这里就要考虑到树dp！！（要是没想到就没了）

我们来考虑下我们要什么，我们需要知道每个点走过所有目标点的最短路程，一个点怎么走完所有的目标点呢？设当前在i点

1. 从点i向上走，走完上面所有目标点后回到i，在从i往下走，走到到达最后一个目标点就停止
2. 从点i向下走，走完下面所有目标点后回到i，在从i点往上走，走到到达最后一个目标点就停止

对于每一个点，我们都是选择这两种走法中的其中一种对不对？那么我们就可以去设计dp的状态了。

f[i] 有三个值
{

1. value,代表从i节点往下走完所有目标点，最后停在离i点最远的目标点后，所走的路程，为什么是最远的目标点？这是一点小贪心，因为我们要距离最短，只要你最长的路走一次就是最短的（不走回头路走两遍），在样例图里面比如f[1]的value就是i走到5，然后停在5，所走的路程是4。
2. judge，**代表的是从i节点往下（包含i节点），存不存在目标点。**为什么要这个变量的原因是方便我们去转移
3. maxlen，代表的是从i节点往下走到停在离i点最远的目标点后，目标点离点i的距离，为什么要设置这个？因为我们的value的权是没有算他走回原点的，但是在后面比如从下走完要继续走上就需要走回原点，这个时候我们就需要去知道他走回原点需要的权值。

}

我们现在是不是设计完从i点走向下的，下一步就是要设计从i点往上走的状态g[i]的值，其实g[i]的所有值都是和f[i]，一样，只是f[i]描述向下，我们g[i]描述向上，其他东西完全不变。
状态设计完了，我们要考虑如何转移
f[i]怎么得到呢，i的儿子f[to]我们算都知道了,那么很明显我们要得到f[i]就需要走完i的所有儿子他们往下所有的目标节点对不对？但是我们儿子的f只是记录从他们自身节点走到最远的目标点，没有走回来，我们需要加上走回来的路程，因为我们一定是走完一个儿子往下的所有目标节点，在走回i，在走下一个儿子的所有目标点那么转移就是

int nowsum = 0, maxlen = 0;
	for (int i = head[now]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == fa)continue;
		if (f[to].judge) {
			nowsum += f[to].value + xian[i].value + f[to].maxlen + xian[i].value;
			maxlen = max(maxlen, xian[i].value + f[to].maxlen);
		}
	}
	f[now].maxlen = maxlen; f[now].value = nowsum - maxlen;

因为我们最后的f[i]还是要在离最远的那个目标节点停下来，所以我们就算出走完所有目标节点后回到i点的值在减去离i最远的目标节点的值，这就是准确的f[i].value；

那么如何算g[i]呢？需要另一张图

假设我们要算节点6的g[i]，那么6往上是2，我们需要利用2的g[2]去统计答案，但是不要忘记另一个需要我们统计的就是，节点2往下的儿子除了节点6的其他目标节点你也得算。
所以要算g[6], 你要利用g[2]和f[3],f[4],就是2节点往上的，和2节点往下的除本节点的f[];
这里的计算方法其实就和上面算f的差不多了

int nowsum = 0, maxlen = 0;
	for (int i = head[fa]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == now || to == father[fa] || !f[to].judge)continue;
		g[now].judge = 1;
		nowsum += f[to].value + f[to].maxlen + xian[i].value * 2;
		maxlen = max(maxlen, f[to].maxlen + xian[i].value + vv[now]);
	}
	if (g[fa].judge) {
		g[now].judge = 1;
		nowsum += g[fa].value + g[fa].maxlen + vv[now] * 2;
		maxlen = max(maxlen, g[fa].maxlen + vv[now]);
	}
	g[now].value = nowsum - maxlen; g[now].maxlen = maxlen;

如果理解f是怎么算的，那么其实g你肯定会，唯一要注意一点的是这个

maxlen = max(maxlen, f[to].maxlen + xian[i].value + vv[now])

vv[now]是什么？，vv[i]表示i与i的父亲所连接的线的权
为什么在这里算maxlen的时候要额外算上这个呢？看图来说就是我们算节点6，我们需要知道节点2往下的其他目标节点（除了6）,但是我们按f的算法那么去算只是算出其他目标节点到2的距离，我们需要的是到6的距离，所以要加上2到6的这段距离。
什么？你问我最后答案是什么？

for (int i = 1; i <= n; i++) {
		printf("%lld\n", f[i].value + g[i].value + g[i].maxlen + f[i].maxlen - max(g[i].maxlen, f[i].maxlen));
	}

我们往下的权和往上的权都加上和maxlen也加上，现在这个价值是什么？i点往上走和往下走完全部目标节点后回到i的权值，我们在减去往下或者往上最远的那个目标节点的距离就好了， 所代表的就是我们最后就停留在这个目标节点上。

AC代码（头文件快读等东西长了点）

#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include
#include 
#include
#include 
#define debug cout<<"*********degug**********";
#define endl "\n"
#define index index_
#define int long long
#define RE register
#define yn yn_
using namespace std;
const long long max_ = 5e5 + 7;
const int mod = 1e9 + 7;
const int inf = 1e9;
const long long INF = 1e18;
int read() {
	int s = 0, f = 1;
	char ch = getchar();
	while (ch<'0' || ch>'9') {
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (ch >= '0'&&ch <= '9') {
		s = s * 10 + ch - '0';
		ch = getchar();
	}
	return s * f;
}
inline int min(int a, int b) {
	return a < b ? a : b;
}
inline int max(int a, int b) {
	return a > b ? a : b;
}
int n, K, head[max_], xiann = 2, aim[max_], father[max_], vv[max_];//vv表示i节点与他的父亲相连的节点的权
struct {
	int next, to, value;
}xian[max_ * 2];
inline void add(int a, int b, int c) {
	xian[xiann].to = b;
	xian[xiann].next = head[a];
	xian[xiann].value = c;
	head[a] = xiann;
	xiann++;
}
struct {
	int value, maxlen, judge;//到达每个目标节点的sum，在与离i点最远的目标节点停止
	//judge = 1表示i往下（包含i）含有目标节点
}f[max_], g[max_];
void dfs(int now, int fa) {
	father[now] = fa;
	if (aim[now])f[now].judge = 1;
	for (int i = head[now]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == fa) { vv[now] = xian[i].value; continue; }
		dfs(to, now);
		f[now].judge |= f[to].judge;
	}
	int nowsum = 0, maxlen = 0;
	for (int i = head[now]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == fa)continue;
		if (f[to].judge) {
			nowsum += f[to].value + xian[i].value + f[to].maxlen + xian[i].value;
			maxlen = max(maxlen, xian[i].value + f[to].maxlen);
		}
	}
	f[now].maxlen = maxlen; f[now].value = nowsum - maxlen;
}
void dfs2(int now, int fa) {
	if (aim[now])g[now].judge = 1;
	int nowsum = 0, maxlen = 0;
	for (int i = head[fa]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == now || to == father[fa] || !f[to].judge)continue;
		g[now].judge = 1;
		nowsum += f[to].value + f[to].maxlen + xian[i].value * 2;
		maxlen = max(maxlen, f[to].maxlen + xian[i].value + vv[now]);
	}
	if (g[fa].judge) {
		g[now].judge = 1;
		nowsum += g[fa].value + g[fa].maxlen + vv[now] * 2;
		maxlen = max(maxlen, g[fa].maxlen + vv[now]);
	}
	g[now].value = nowsum - maxlen; g[now].maxlen = maxlen;
	for (int i = head[now]; i; i = xian[i].next) {
		int to = xian[i].to;
		if (to == fa)continue;
		dfs2(to, now);
	}
}
signed main() {
	n = read(), K = read();
	for (int i = 2; i <= n; i++) {
		int a = read(), b = read(), c = read();
		add(a, b, c); add(b, a, c);
	}
	for (int i = 1; i <= K; i++) {
		aim[read()] = 1;
	}
	dfs(1, 0);
	dfs2(1, 0);
	/*for (int i = 1; i <= n; i++) {
		cout << i << "个点f:" << f[i].maxlen << " " << f[i].value << endl;
	}
	for (int i = 1; i <= n; i++) {
		cout << i<< "个点g:"<< g[i].maxlen << " " << g[i].value << endl;
	}*/
	for (int i = 1; i <= n; i++) {
		printf("%lld\n", f[i].value + g[i].value + g[i].maxlen + f[i].maxlen - max(g[i].maxlen, f[i].maxlen));
	}
	return 0;
}