HNUCM2020年春季ACM集训队热身赛-第9场题解

问题 A: 循环数比较

题目描述

对于任意两个正整数x和k,我们定义repeat(x, k)为将x重复写k次形成的数,例如repeat(1234, 3) = 123412341234,repeat(20,2) = 2020.
牛牛现在给出4个整数x1, k1, x2, k2, 其中v1 = (x1, k1), v2 = (x2, k2),请你来比较v1和v2的大小。

输入

多组输入
输入包括一行,一行中有4个正整数x1, k1, x2, k2(1 ≤ x1,x2 ≤ 10^9, 1 ≤ k1,k2 ≤ 50),以空格分割。

输出

如果v1小于v2输出"Less",v1等于v2输出"Equal",v1大于v2输出"Greater".

样例输入

1010 3 101010 2

样例输出

Equal

先判断长度，长度大的肯定就大，如果长度一样就把循环后的数字算出来，再比较…数字比较大，要用数组存

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
int get(int x){//获取数字x的长度
    int num=0;
    while(x){
        ++num;
        x/=10;
    }
    return num;
}
int aa[15],cc[15],la,lc;
int A[maxn],C[maxn],LA,LC;
int ju(){//如果A和C长度相等判断A和C的大小
    for(int i=1;i<=LA;++i){
        if(A[i]>C[i])return 3;
        else if(A[i]<C[i])return 1;
    }
    return 2;
}
int main()
{
    int a,b,c,d;
    while(~scanf("%d %d %d %d",&a,&b,&c,&d)){
        la=get(a),lc=get(c);//获取a和c的长度
        if(la*b>lc*d){//a循环b次的长度比c循环d次的长度长直接输出Greater
            printf("Greater\n");
            continue;
        }else if(la*b<lc*d){//a循环b次的长度比c循环d次的长度短直接输出Less
            printf("Less\n");
            continue;
        }
        //如果一样长就把循环后的数字计算出来在比较
        for(int i=la;i>=1;--i){//将a拆分成一位位的存到数组aa中
            aa[i]=a%10;
            a/=10;
        }
        for(int i=lc;i>=1;--i){//将c拆分成一位位的存到数组cc中
            cc[i]=c%10;
            c/=10;
        }
        for(int i=1;i<=b;++i){//将aa循环b次存到A中
            for(int j=1;j<=la;++j){
                A[(i-1)*la+j]=aa[j];
            }
        }
        for(int i=1;i<=d;++i){//将cc循环d次存到C中
            for(int j=1;j<=lc;++j){
                C[(i-1)*lc+j]=cc[j];
            }
        }
        LA=la*b;
        LC=lc*d;
        //ju()比较A和C的大小
        if(ju()==1){
            printf("Less\n");
        }else if(ju()==2){
            printf("Equal\n");
        }else{
            printf("Greater\n");
        }
    }
    return 0;
}

问题 B: 小易喜欢的数列

题目描述

小易非常喜欢拥有以下性质的数列:
1、数列的长度为n
2、数列中的每个数都在1到k之间(包括1和k)
3、对于位置相邻的两个数A和B(A在B前),都满足(A <= B)或(A mod B != 0)(满足其一即可)
例如,当n = 4, k = 7
那么{1,7,7,2},它的长度是4,所有数字也在1到7范围内,并且满足第三条性质,所以小易是喜欢这个数列的
但是小易不喜欢{4,4,4,2}这个数列。小易给出n和k,希望你能帮他求出有多少个是他会喜欢的数列。

输入

多组输入
输入包括两个整数n和k(1 ≤ n ≤ 10, 1 ≤ k ≤ 10^5)。

输出

输出一个整数,即满足要求的数列个数,因为答案可能很大,输出对1,000,000,007取模的结果。

样例输入

2 2

样例输出

3

dp问题
考虑相邻的两个数字A和B，需要保证A<=B或A%B!=0
也就是后一个数不能是前一个数的因子
求因子的时间复杂度为sqrt(n)
时间复杂度比较大（会超时）

考虑反向，从后往前求，那限制条件也就变成了B<=A或B%A!=0
也就是后一个不能是前一个数的倍数
这样求因子就变成了求倍数
具体复杂度是多少不太好证明（好吧…是我不会证）
不过能感觉出来有一定程度的优化了
状态转移方程

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
const int mod=1000000007;
ll num[15][maxn];//num[i][j]表示第i个数字是j的数列种数
int main()
{
    int n,k;
    while(~scanf("%d %d",&n,&k)){
        for(int i=1;i<=k;++i)num[1][i]=1;//初始化，一个数字的时候都是1
        for(int i=2;i<=n;++i){
            ll all=0;
            for(int j=1;j<=k;++j)all=(all+num[i-1][j])%mod;//统计前一个数字所有的种数
            for(int j=1;j<=k;++j){
                num[i][j]=all;
               
                //B不能是A的倍数
                for(int p=j+j;p<=k;p+=j){//去掉A的倍数
                    num[i][j]=(num[i][j]-num[i-1][p]+mod)%mod;//num[i][j]-num[i-1][p]可能是负数需要+mod再取模
                }
            }
        }
        ll ans=0;
        for(int i=1;i<=k;++i)ans=(ans+num[n][i])%mod;//统计所有种数
        printf("%lld\n",ans);
    }
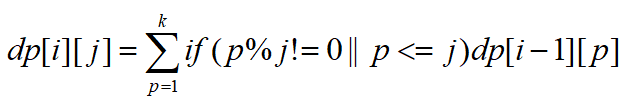
    return 0;
}

问题 C: 堆棋子

题目描述

小易将n个棋子摆放在一张无限大的棋盘上。第i个棋子放在第x[i]行y[i]列。同一个格子允许放置多个棋子。每一次操作小易可以把一个棋子拿起并将其移动到原格子的上、下、左、右的任意一个格子中。小易想知道要让棋盘上出现有一个格子中至少有i(1 ≤ i ≤ n)个棋子所需要的最少操作次数。

输入

多组输入
输入包括三行,第一行一个整数n(1 ≤ n ≤ 50),表示棋子的个数
第二行为n个棋子的横坐标x[i](1 ≤ x[i] ≤ 10^9)
第三行为n个棋子的纵坐标y[i](1 ≤ y[i] ≤ 10^9)

输出

输出n个整数,第i个表示棋盘上有一个格子至少有i个棋子所需要的操作数,以空格分割。行末无空格

如样例所示:
对于1个棋子: 不需要操作
对于2个棋子: 将前两个棋子放在(1, 1)中
对于3个棋子: 将前三个棋子放在(2, 1)中
对于4个棋子: 将所有棋子都放在(3, 1)中

样例输入

4
1 2 4 9
1 1 1 1

样例输出

0 1 3 10

首先行和列都是独立的
最后移动到的格子所在的行和列都会有其他棋子…不太好证明，仔细想想差不多就理解了
枚举所有的行列计算操作数…

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
const int mod=1000000007;
ll x[55],y[55],a[55],ans[55];
int main()
{
    int n;
    while(~scanf("%d",&n)){
          
        for(int i=1;i<=n;++i)ans[i]=1e18;
        for(int i=1;i<=n;++i)scanf("%lld",&x[i]);
        for(int i=1;i<=n;++i)scanf("%lld",&y[i]);
        for(int i=1;i<=n;++i){//枚举行
            for(int j=1;j<=n;++j){//枚举列
                for(int k=1;k<=n;++k){//计算每一个棋子到点(x[i],y[j])的步数
                    a[k]=abs(x[i]-x[k])+abs(y[j]-y[k]);
                }
                sort(a+1,a+n+1);//将步数排序
                ll all=0;
                for(int k=1;k<=n;++k){//计算k个棋子在同一个点的最小步数
                    all+=a[k];
                    ans[k]=min(ans[k],all);
                }
            }
        }
        for(int i=1;i<=n;++i)printf("%lld%c",ans[i],i==n?'\n':' ');
    }
    return 0;
}

问题 D: 交错01串

题目描述

如果一个01串任意两个相邻位置的字符都是不一样的,我们就叫这个01串为交错01串。例如: “1”,“10101”,"0101010"都是交错01串。
小易现在有一个01串s,小易想找出一个最长的连续子串,并且这个子串是一个交错01串。小易需要你帮帮忙求出最长的这样的子串的长度是多少。

输入

多组输入
输入包括字符串s,s的长度length(1 ≤ length ≤ 50),字符串中只包含’0’和’1’。

输出

输出一个整数,表示最长的满足要求的子串长度。

样例输入

111101111

样例输出

3

遍历数组，维护一下长度即可

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
char s[55];
int main()
{
    while(~scanf("%s",s+1)){
        int ls=strlen(s+1),ans=1,now=1;
        for(int i=2;i<=ls;++i){
            if(s[i]!=s[i-1])++now;//如果和前一个不一样那就接在前一个的后面组成更长的01串
            else ans=max(ans,now),now=1;//否则从当前开始
        }
        ans=max(ans,now);
        printf("%d\n",ans);
    }
    return 0;
}

问题 E: 就不喜欢66

题目描述

众所周知，牛牛不喜欢6这个数字（因为牛牛和66发音相近）。
所以他想知道，不超过n位十进制数中有多少个数字不含有连续的6（从1开始算的）。

输入

输入只包含一个正整数n（1<=n<20）。

输出

满足条件的数字个数。

样例输入

1
2​

样例输出

10
99

提示

个位数中，1,2,3,4,5,6,7,8,9,10 这十个数字中都满足条件。十位数中66不满足条件。

dp问题
状态转移dp[i][j]=∑if(k!=6||j!=6)dp[i-1][k]

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
ll num[55][55];
int main()
{
    int n;
    while(cin>>n){
        memset(num,0,sizeof(num));
        for(int i=1;i<=9;++i)num[1][i]=1;
        ll ans=0;
        for(int i=2;i<=n;++i){
            for(int j=0;j<=9;++j){
                for(int k=0;k<=9;++k){
                    if(j!=6||k!=6)//如果是连续的6不统计
                        num[i][j]=num[i][j]+num[i-1][k];
                }
            }
        }
        for(int i=1;i<=n;++i)for(int j=0;j<=9;++j)ans=ans+num[i][j];
        cout<<ans+1<<endl;//用printf会输出超限
    }
    return 0;
}

问题 F: 递增数组

题目描述

牛牛有一个数组array，牛牛可以每次选择一个连续的区间，让区间的数都加1，他想知道把这个数组变为严格单调递增，最少需要操作多少次？

输入

输入一个整型数组，数组大小<=10⁵，数组元素的值<=10⁹。

输出

返回最少操作次数。

样例输入

1 2 1

样例输出

2

提示

把第三个数字+2可以构成1，2，3。

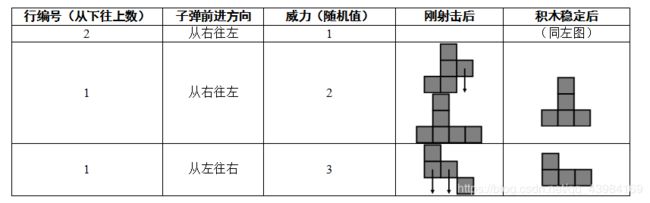
从左到右考虑，如果碰到前一个>=后一个，那肯定需要将后一个增加到>前一个为止，增加的时候避免影响后面的可以将当前到最后整个区间都加1，这样只需要统计a[i-1]-a[i]+1 if(a[i]

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
int a[maxn];
int main()
{
    int cnt=0,x;
    while(~scanf("%d",&x)){
        a[++cnt]=x;
    }
    ll ans=0,now=0;
    for(int i=2;i<=cnt;++i){
        if(a[i]<=a[i-1])ans+=a[i-1]-a[i]+1;
    }
    printf("%lld\n",ans);
    return 0;
}

问题 G: 三色球

题目描述

有红、黄、蓝三种颜色的气球。
在牛客王国，1个红气球+1个黄气球+1个蓝气球可以兑换一张彩票。
2个红气球+1个黄气球可以兑换1个蓝气球。
2个黄气球+1个蓝气球可以兑换1个红气球。
2个蓝气球+1个红气球可以兑换1个黄气球。
现在牛牛有a个红气球，b个黄气球， c个蓝气球，牛牛想知道自己最多可以兑换多少张彩票。

输入

每一组输入包括3个正整数，分别表示红气球、黄气球和蓝气球的个数。
输出
对于每一组输入，输出最多可以兑换的彩票数量。

样例输入

1 7 5

样例输出

3

提示

可以用4个黄气球和2个蓝气球换2个红气球，这样就有了3个红气球，3个黄气球，3个蓝气球，可以换3张彩票。

先尽量用1个红气球+1个黄气球+1个蓝气球换
然后有三种兑换方式
1红+1黄+（2红+1黄（蓝））
1红+1蓝+（2蓝+1红（黄））
1蓝+1黄+（2黄+1蓝（红））

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
int a[maxn];
int main()
{
    int a,b,c;
    while(~scanf("%d %d %d",&a,&b,&c)){
        int ans=min(a,min(b,c));
        a-=ans;
        b-=ans;
        c-=ans;
        if(a&&b){
            ans+=min(a/3,b/2);
        }else if(b&&c){
            ans+=min(b/3,c/2);
        }else if(a&&c){
            ans+=min(c/3,a/2);
        }
        printf("%d\n",ans);
    }
    return 0;
}

问题 H: 好多牛牛

题目描述

给出一个字符串S，牛牛想知道这个字符串有多少个子序列等于"niuniu"。
子序列可以通过在原串上删除任意个字符(包括0个字符和全部字符)得到。
为了防止答案过大，答案对1e9+7取模。

输入

输入一个字符串，字符串长度<=10^5。

输出

输出等于"niuniu"的子序列个数。

样例输入

niuniniu

样例输出

3

提示

删除第4，5个字符可以得到"niuniu"。
删除第5，6个字符可以得到"niuniu"。
删除第6，7个字符可以得到"niuniu"。

dp~
a[1]表示子序列n的数量 if(当前点是n)那a[1]++
a[2]表示子序列ni的数量 if(当前点是i)那a[2]+=a[1]
a[3]表示子序列niu的数量 if(当前点是u)那a[3]+=a[2]
a[4]表示子序列niun的数量 if(当前点是n)那a[4]+=a[3]
a[5]表示子序列niuni的数量 if(当前点是i)那a[5]+=a[4]
a[6]表示子序列niuniu的数量 if(当前点是u)那a[6]+=a[5]

#include
#define ll long long
using namespace std; 
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
const int mod=1000000007;
ll a[15];
char s[maxn];
int main()
{
    while(~scanf("%s",s+1)){
        memset(a,0,sizeof(a));
        int ls=strlen(s+1);
        for(int i=1;i<=ls;++i){
            if(s[i]=='n'){
                a[4]=(a[4]+a[3])%mod;
                ++a[1];
            }else if(s[i]=='i'){
                a[5]=(a[5]+a[4])%mod;
                a[2]=(a[2]+a[1])%mod;
            }else if(s[i]=='u'){
                a[6]=(a[6]+a[5])%mod;
                a[3]=(a[3]+a[2])%mod;
            }
        }
        printf("%lld\n",a[6]);
    }
      
    return 0;
}

问题 I: 射击游戏

题目描述

A和B在玩一个射击游戏，战场由若干单位正方形积木组成。积木占据了连续的若干列，且图形周长等于它最小包围矩形的周长。下图(a)是一个合法的战场，但(b)和©都不是：(b)中有空列；©的图形周长为14，而最小包围矩形（用虚线画出）的周长为12。受重力影响，每个积木的正下方要么是地面，要么是另一个积木。为了让战场看上去错落有致、玩着更刺激，它不能恰好是一个矩形（即：不能每列积木都一样高）。

游戏规则如下：

1、 A和B轮流射击，A先射击。

2、 每次射击时，首先选择一行（该行必须至少有一个积木），以及“左”和“右”中的一个方向，然后往这个方向开火。子弹的威力为1~3的均匀随机整数（即：威力为1、2、3的概率各为1/3），表示子弹能打掉的积木个数，被打掉的积木将直接从战场中消失。如果该行的积木个数小于威力值，则子弹将在打掉该行所有积木后消失。例如，若选择往右射击从下往上数第3行，且威力为2，且这一行一共有4个积木，则最左边的两个积木将被打掉。注意：这两个积木可以不连续。

3、 每次射击完成后，悬空的积木垂直往下落。所有积木不再下落后，下一位选手才能开始射击。

4、 谁打掉了最后一个积木，谁就获胜。

假定开局是，根据规则1，A先开火。射击后，B可能面临的后续局面中的其中三个如下表：

假定A和B都足够聪明，采取让自己获胜概率尽量高的策略，你的任务是计算出A获胜的概率。

输入

输入文件最多包含25组测试数据，每个数据仅包含两行，第一行是整数n（1<=n<=6），即积木的列数。第二行包含n个正整数h1, h2,…, hn(1<=hi<=6)，表示从左往右数第i列的高度。积木的排列方式保证符合题目描述（即：图形周长等于它最小包围矩形的周长，且各列的高度不全相同）。n=0表示输入结束，你的程序不应当处理这一行。

输出

对于每组数据，输出仅一行，即A获胜的概率，四舍五入保留六位小数。

样例输入

3
2 1 1
0

样例输出

0.555556

dfs模拟

#include
#define ll long long
using namespace std;
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
int n;
double dp[10][10][10][10][10][10];
double dfs(int *h){
    if(dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]]!=-1)return dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]];//记忆化
    dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]]=0;
    for(int i=1;i<=6;++i){
        int num=0;
        double ans=0;
        for(int j=0;j<6;++j)if(h[j]>=i){++num;};
        if(num==0)break;
        for(int j=1;j<=3;++j){
            int hh[10];
            for(int k=0;k<6;++k)hh[k]=h[k];
            num=j;
            for(int k=0;k<6&&num;++k){
                if(hh[k]>=i){
                    --num;
                    --hh[k];
                }
            }
            ans+=1.0-dfs(hh);//因为是轮流操作，每一次递归都用1-概率（对手赢的概率是x那自己就是1-x咯）
        }
        //左->右开枪
        dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]]=max(dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]],ans/3.0);
        ans=0;
        for(int j=1;j<=3;++j){
            int hh[10];
            for(int k=0;k<6;++k)hh[k]=h[k];
            num=j;
            for(int k=5;k>=0&&num;--k){
                if(hh[k]>=i){
                    --num;
                    --hh[k];
                }
            }
            ans+=1.0-dfs(hh);
        }
        //右->左开枪
        dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]]=max(dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]],ans/3.0);
    }
    return dp[h[0]][h[1]][h[2]][h[3]][h[4]][h[5]];
}
int main()
{
    int h[10];
    while(~scanf("%d",&n)&&n){
        memset(h,0,sizeof(h));
        for(int i=0;i<n;++i)scanf("%d",&h[i]);
        //初始化-1,memset初始化有点问题（不明原因）
        for(int i=0; i<=6; i++)
            for(int j=0; j<=6; j++)
                for(int k=0; k<=6; k++)
                    for(int l=0; l<=6; l++)
                        for(int q=0; q<=6; q++)
                            for(int w=0; w<=6; w++)
                                dp[i][j][k][l][q][w]=-1;
        printf("%.6lf\n",dfs(h));
    }
    return 0;
}

问题 J: 战场的数目

题目描述

在上题中，假设战场的图形周长为p，一共有多少种可能的战场？
例如，p<8时没有符合要求的战场，p=8时有2种战场：

p=10有9种战场：

要求输出方案总数模987654321的值。

输入

输入文件最多包含25组测试数据，每个数据仅包含一行，有一个整数p（1<=p<=109），表示战场的图形周长。p=0表示输入结束，你的程序不应当处理这一行。

输出

对于每组数据，输出仅一行，即满足条件的战场总数除以987654321的余数。

样例输入

7
8
9
10
0

样例输出

0
2
0
9

dp[i]表示周长为2*i的种数
考虑最底下一行
1.如果最左边的高度是1将其删去，+dp[i-1]
2.如果最右边的高度是1将其删去，+dp[i-1]
3.删去底下一行，+dp[i-1]
如果左右两边的高度都是1，这种在1，2重复了需要减去，-dp[i-2]
状态转移方程为dp[i]=3*dp[i-1]-dp[i-2]
易知i=4时的种类数为5，i=5时的种类数为13，
数字很大，需要矩阵快速幂优化
构造初始化矩阵

构建幂矩阵

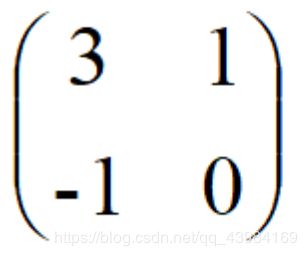
最后还需要减去矩形的数量，这种类型不合题意
周长为i的有i/2-1种矩形种类
证明
x=i/2（i肯定是偶数）
长p可以选择1到x-1宽q也就被确定了，q=x-p
也就是有x-1种，也就是i/2-1

#include
#define ll long long
using namespace std;
const int maxn=1e5+5;
const int inf=0x3f3f3f3f;
const int mod=987654321;
struct node{
    ll x[2][2];
    node(){
        memset(x,0,sizeof(x));
    }
    node operator*(const node p)const{//重载乘法
        node ans;
        for(int i=0;i<2;++i)
            for(int j=0;j<2;++j)
                for(int k=0;k<2;++k)
                    ans.x[i][j]=(ans.x[i][j]+x[i][k]*p.x[k][j])%mod;
        return ans;
    }
};
node k,st;
node pow_(int b){
    node ans=st,a=k;
    while(b){
        if(b&1)ans=ans*a;
        a=a*a;
        b>>=1;
    }
    return ans;
}
int main()
{
    int p;
    st.x[0][0]=13,st.x[0][1]=5;
    k.x[0][0]=3,k.x[0][1]=1,k.x[1][0]=-1;
    while(~scanf("%d",&p)&&p){
        if(p<8||p&1){
            printf("0\n");
            continue;
        }
        p>>=1;
        node ans=pow_(p-4);
        printf("%lld\n",(ans.x[0][1]+mod-(p-1)%mod)%mod);
    }
    return 0;
}