WaWa的奇妙冒险（第十一周集训自闭现场）

（一）LCA（简单题）

1.反向求同一最近公共祖先下有多少对组合

洛谷 P5002 专心OI - 找祖先
链接 https://www.luogu.org/problem/P5002

题意：求出以x为最近公共祖先的组合有多少对

理解：
此处借用洛谷的原图讲一下思路：

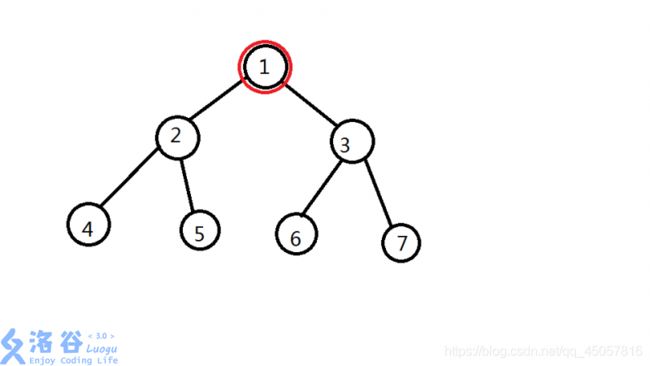
算所有组合对，我们可以发现，是根结点单独做一个集合，然后每一棵子树做一个集合之后，每个集合和非自身集合的乘积的和的和。但这样处理起来很麻烦，观察发现，只要对每次新进来的子树和原有的所有点算一次乘积然后乘2即可，这样累加即可得到最终结果。

只要预处理所有的点，然后就可以直接进行查询了。

#include 
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int maxn = 1e4+5;

struct edg{
	int to,next;
} e[maxn*10];
int head[maxn],dep[maxn];
ll ans[maxn];
int tot;

void init(int n){
	tot = 0;
	e[0].to = 0;e[0].next = 0;
	for(int i = 1;i <= n;++i) head[i] = 0,dep[i] = 0,ans[i] = 1;
	return ;
}

void add(int u,int v){
	e[++tot].to = v;
	e[tot].next = head[u];
	head[u] = tot;
	return ;
}

void dfs(int u,int f){  要记录f结点，f结点不能计入子树内
	dep[u] = 1;
	for(int i = head[u];i;i = e[i].next){
		int v = e[i].to;
		if(v == f) continue;
		dfs(v,u);
		ans[u] += dep[u]*dep[v]*2;
		ans[u] %= mod;
		dep[u] += dep[v];
	}
	return ;
}

int main(){
	
	int u,v,n,r,m;
	scanf("%d%d%d",&n,&r,&m);
	init(n);
	
	for(int i = 1;i < n;++i){
		scanf("%d%d",&u,&v);
		add(u,v);
		add(v,u);
	}
	
	dfs(r,0);
	
	for(int i = 0;i < m;++i){
		scanf("%d",&u);
		printf("%d\n",ans[u]);
	}
	return 0;
}

2.路径带权的LCA

洛谷 P1967 货车运输
链接 https://www.luogu.org/problem/P1967

题意：要求求出从u到v路上最小的边权为多少

思路：
第一次做边带权LCA其实还是有点懵逼，但仔细想想，之前写LCA的倍增实际上就边权为1的树（deep），而用deep表示边权为1，可以采用转边权为点权的方式，然后维护根结点为0点权（转RMQ），也可以干脆以RMQ记边权，这两者本质上写起来来是一样的，就是想得思路上有所区别

#include 
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int maxn = 1e4+5;

struct edg{
	int from,to,dis,next;
} e[maxn*10],te[maxn*10];
int dep[maxn],head[maxn],pre[maxn],p[maxn][20],d[maxn][20];
int tot;

void init(int n){
	tot = 0;
	e[0].to = 0;e[0].next = 0;
	te[0].to = 0;te[0].next = 0;
	for(int i = 1;i <= n;++i) head[i] = 0,dep[i] = 0,pre[i] = i;
	memset(p,0,sizeof(p));
	memset(d,INF,sizeof(d));
	return ;
}

void add(int u,int v,int d){
	te[++tot].to = v;
	te[tot].next = head[u];
	te[tot].dis = d;
	head[u] = tot;
	return ;
}

void dfs(int u){
	for(int i = head[u];i;i = te[i].next){
		int v = te[i].to;
		if(!dep[v]){
			dep[v] = dep[u]+1;  ##  记录深度
			p[v][0] = u;  ##  倍增法的记录父节点
			d[v][0] = te[i].dis;  ##  RMQ记录边权
			dfs(v);
		}
	}
	return ;
}

bool comp(edg x,edg y){
	return x.dis > y.dis;
}

int find(int x){
	return pre[x] = pre[x] == x ?x :find(pre[x]);
}

void kal(int n){  ##  建立最大生成树
	sort(e+1,e+n+1,comp);
	for(int i = 1;i <= n;++i){
		int u = e[i].from;
		int v = e[i].to;
		if(pre[find(u)] == pre[find(v)]) continue;
		pre[find(u)] = pre[find(v)];
		//cout << "111 " << u << " " << v << " " << e[i].dis << endl;
		add(u,v,e[i].dis);
		add(v,u,e[i].dis);
	}
	return ;
}

void change(int n){  ##  预处理dp数组（RMQ）
	for(int i = 1;(1 << i) <= n;++i){
		for(int j = 1;j <= n;++j){
			if(p[j][i-1]){
				p[j][i] = p[p[j][i-1]][i-1];
				d[j][i] = min(d[j][i-1],d[p[j][i-1]][i-1]);
			}
		}
	}
	return ;
}

int lca(int u,int v){
	int ans = INF;
	if(dep[u] > dep[v]) swap(u,v);
	int len = dep[v] - dep[u];
	//cout << "len = " << len << endl;
	for(int i = len,j = 0;i;i >>= 1,++j){
		//cout << v << " " << j << " " << d[v][j] << endl;
		if(i & 1) ans = min(ans,d[v][j]),v = p[v][j];
	}
	
	if(u == v) return ans;
	for(int i = 19;i >= 0;--i){
		//cout << p[u][i] << " " << p[v][i] << endl;
		if(p[u][i] == p[v][i]) continue;
		ans = min(ans,min(d[u][i],d[v][i]));
		u = p[u][i];
		v = p[v][i];
	}
	ans = min(ans,min(d[u][0],d[v][0]));
	return ans;
}

int main(){
	int u,v,n,m,q;
	scanf("%d%d",&n,&m);
	init(n);
	
	for(int i = 1;i <= m;++i)
		scanf("%d%d%d",&e[i].from,&e[i].to,&e[i].dis);	
	
	kal(m);
	
	for(int i = 1;i <= n;++i){
		if(pre[find(i)] == i){
			dep[i] = 1;
			dfs(i);
		}
	}
	
	change(n);
	
	scanf("%d",&q);
	while(q--){
		scanf("%d%d",&u,&v);
		if(pre[find(u)] == pre[find(v)]) printf("%d\n",lca(u,v));
		else printf("-1\n");
	}
	
	return 0;
}

（二）RMQ

RMQ算法的实质实际上就是二分思想加上区间dp的结合，在理解RMQ之前，不然先思考，如何用logn的复杂度查找区间内的最大值和最小值，对于理解RMQ会有很大的帮助

板子和讲解也很多，这边就不讲了，估计也没别人讲的好
https://blog.csdn.net/Sclong0218/article/details/97036282 这里贴一个感觉讲的简单易懂，模板也还行的blog

RMQ写的例题没几道，都很水，但有一道卡了RMQ，用了单调队列才写出来（也是人生第一次写单调队列），姑且记录一下

洛谷 P1440 求m区间内的最小值
链接 https://www.luogu.org/problem/P1440

80分代码（RMQ） mle两个点（没想通为啥会mle两个点。。。）

#include 
using namespace std;
const int maxn = 2e6+5;
const int INF = 0x3f3f3f3f;

int p[maxn][20];

int RMQ(int l,int r){
	if(r < l) return 0;
	int k = log(r-l+1)/log(2);
	//cout << l << " " << r-(1 << k)+1 << endl;
	return min(p[l][k],p[r-(1 << k)+1][k]);
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	
	for(int i = 1;i <= n;++i) scanf("%d",&p[i][0]);
	
	for(int i = 1;(1 << i) <= n;++i){
		for(int j = 1;j+(1 << i)-1 <= n;++j){
			p[j][i] = min(p[j][i-1],p[j+(1 << (i-1))][i-1]);
		}
	}
	
	printf("0\n");
	for(int i = 1;i < n;++i){
		printf("%d\n",RMQ(max(1,i-m+1),i));
	}
	return 0;
}

100分代码（单调队列，数组模拟队列）

#include 
using namespace std;
const int maxn = 2e6+10;

int Que[maxn][2],a[maxn];

int main()
{
	int n,m,tot = 1,head = 1;
	scanf("%d%d",&n,&m);
	printf("0\n");
	for(int i = 1;i <= n;++i) scanf("%d",&a[i]);
	
	Que[head][0] = a[1],Que[head][1] = 1,printf("%d\n",a[1]);
	for(int i = 2;i < n;++i){
		if(i - Que[head][1] >= m) head++;
		if(a[i] > Que[tot][0]) Que[++tot][0] = a[i],Que[tot][1] = i;
		else{
			while(tot >= head && Que[tot][0] > a[i]) tot--;
			Que[++tot][0] = a[i];
			Que[tot][1] = i;
		}
		printf("%d\n",Que[head][0]);
	}
	return 0;	
}

（三）单调队列、单调栈、尺取法

目前个人理解的单调队列、单调栈都是一种维持容器内单调性而达成某种目的的方式，但emm 因为实际上没写过多少题，也总结不出来什么东西，暂且不表、下周刷点题，再仔细讲讲

尺取法刷单调队列的水题的时候遇到了一道，实际上尺取法个人认为就是单调队列的一种变形？或者说是师出同源，都是一种动态框移动的思路

简单贴一道做到的尺取法的水题

洛谷 P1638 逛画展
链接 https://www.luogu.org/problem/P1638

思路，维护一个拥有所有画家画的集合就可以了

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 1e6+5;

int a[maxn],v[2005];

int main()
{
	//freopen("test.in","r",stdin);
	
	int n,m,sum = 0;
	scanf("%d %d",&n,&m);
	memset(v,0,sizeof(v));
	
	for(int i = 1;i <= n;++i) scanf("%d",&a[i]);
	int l = 1,r = 1,ansl = 1,ansr = 1,len = 0x3f3f3f3f;
	v[a[1]]++;sum++;
	while(1){
		if(r >= n) break;
		while(sum < m && r < n){
			r++;
			if(!v[a[r]]) sum++;
			v[a[r]]++;
		}

		while(sum == m && l <= n){
			if(r-l < len) len = r-l,ansl = l,ansr = r;
			v[a[l]]--;
			if(!v[a[l]]) sum--;
			l++;
		}
	}
	
	printf("%d %d\n",ansl,ansr);
	return 0;
}

（四）训练赛题目记录

1.状态背包（状压背包？）

CCPC秦皇岛Invoker

题意：每种特殊技能能由三种小技能的组合（无循序要求）释放，小技能的槽位只有三个，新的小技能会会顶掉技能槽里第一个技能

思路：技能槽只有三个槽位，而小技能只有三个，所以实际上对于每个特殊技的释放条件只有六种可能性，所以实际上就是一个状态背包dp，之所以想叫状压，是因为把原来字母的状态存了一下，然后用数字表示，方便了dp

#include 
using namespace std;
const int maxn = 1e6+5;
const int INF = 0x3f3f3f3f;

int s[maxn];
int dp[maxn][6];
map <char,int> p;
string zt[10][6] = {"QQQ","QQQ","QQQ","QQQ","QQQ","QQQ",
                    "QQW","QWQ","QQW","QWQ","WQQ","WQQ",
                    "QQE","QEQ","QQE","QEQ","EQQ","EQQ",
                    "WWW","WWW","WWW","WWW","WWW","WWW",
                    "QWW","QWW","WQW","WWQ","WQW","WWQ",
                    "WWE","WEW","WWE","WEW","EWW","EWW",
                    "EEE","EEE","EEE","EEE","EEE","EEE",
                    "QEE","QEE","EQE","EEQ","EQE","EEQ",
                    "WEE","WEE","EWE","EEW","EWE","EEW",
                    "QWE","QEW","WQE","WEQ","EQW","EWQ"};
                    
void init(){
    p['Y'] = 0;p['V'] = 1;p['G'] = 2;p['C'] = 3;p['X'] = 4;
    p['Z'] = 5;p['T'] = 6;p['F'] = 7;p['D'] = 8;p['B'] = 9;
}
    
int dis(int s1,int s2,int k,int j){
    if(zt[s1][k][1] == zt[s2][j][0] && zt[s1][k][2] == zt[s2][j][1]) return 1;
    if(zt[s1][k][2] == zt[s2][j][0]) return 2;
    return 3;
}
                
int main()
{
    string str;
    while(cin >> str){
        init();
        int len = str.size(),slen = 0,ans = len;
        s[slen++] = p[str[0]];
        for(int i = 1;i < len;++i){
            if(str[i] != str[i-1]) s[slen++] = p[str[i]];
        }
        
        for(int i = 0;i < slen;++i){
            for(int j = 0;j < 6;++j){
                dp[i][j] = INF;
            }
        }
        dp[0][0] = dp[0][1] = dp[0][2] = dp[0][3] = dp[0][4] = dp[0][5] = 3;
        
        for(int i = 1;i < slen;++i){
            for(int j = 0;j < 6;++j){
                for(int k = 0;k < 6;++k){
                    dp[i][j] = min(dp[i][j],dp[i-1][k] + dis(s[i-1],s[i],k,j));
                }
            }
        }
        
        int mins = dp[slen-1][0];
        for(int i = 0;i < 6;++i){
            mins = min(mins,dp[slen-1][i]);
        }
        printf("%d\n",ans+mins);
    }
    
    return 0;
}

2.玄学退火

2018icpc南京 D Country Meow

题意：求最小球覆盖的半径

思路：。。。怎么说呢，对于整个队都不会计算几何的蒟蒻队来说，正常写法真的写不来，看了一下，误差在1e-3范围内即可，拉了之前写的求最小圆覆盖的退火模板，结果一波ac，很nice

pis：对于精度要求高的题目，请谨慎使用退火，精度高的情况下，参数能不能导出正确答案十分看运气，在实在无题可做的情况下，再去用退火莽。。。

#include 
#include 
#include 
using namespace std;
const double eps = 1e-15;

struct node{
	double x,y,z;
} a[105];

double dis(node a,node b){return sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2)+pow(a.z-b.z,2));}

double SA(int x,int y,int z,int n){
	double T = 100000;
	double delta = 0.98;
	double r = 0x3f3f3f3f;
	node g;
	g.x = x;g.y = y;g.z = z;
	while(T > eps){
		int k = 0;
		double d = 0;
		for(int i = 0;i < n;++i){
			double f = dis(g,a[i]);
			if(f > d){
				d = f;
				k = i;
			}
		}
		r = min(r,d);
		g.x += (a[k].x - g.x) / d * T;
		g.y += (a[k].y - g.y) / d * T;
		g.z += (a[k].z - g.z) / d * T;
		T *= delta;
	}
	return r;
}

int main()
{
	double ax = 0,ay = 0,az = 0;
	int n;
	scanf("%d",&n);
	for(int i = 0;i < n;++i){
		scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].z);
		ax += a[i].x;
		ay += a[i].y;
		az += a[i].z;
	}
	ax /= 1.0*n;ay /= 1.0*n;az /= 1.0*n;
	double ans = SA(ax,ay,az,n);
	printf("%.15f\n",ans);
	return 0;
} 

退火板子emm 就不讲了，稍微学过点的都能打板子，类型也比较死。

3.差分方程

2018icpc南京 G Pyramid

题意：按要求建图，问图中有几个等边三角形

思路：刚开始想的递推，统计三角形和六边形的数量，推出答案，发现数据规模太大，递推必然超时。（这时沈大佬发话说是差分方程，后面大概问了一下，就是按层数增加（n-x），直到变成一个线性方程为止，而线性方程每一步的增量就是其一次项的系数）。

最后可以得到公式:(n-1)(n-2)(n-3)(ax + b) = ans

代入数据算出a和b即可，然后就可以通过简单的计算得到答案

#include 
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;

ll qpow(ll a,ll b){
	ll res = 1;
	while(b){
		if(b & 1) res = (res*a)%mod;
		a = (a*a)%mod;
		b >>= 1;
	}
	return res;
}
ll inv(ll a){return qpow(a,mod-2);}

int main()
{
	ll t,n;
	scanf("%lld",&t);
	while(t--){
		scanf("%lld",&n);
		printf("%lld\n",(n+1)%mod*(n+2)%mod*(n+3)%mod*n%mod*inv(24)%mod);
	}
	return 0;
}

4.数据规模的特性

其实记录这个总感觉有点玄乎，因为他貌似并非是一种正解，但确实可以达到ac的目的，不知道该说是利用了出题人的思维漏洞，还是说这本来就是出题人留给选手的伪装的极好的思维题

2018icpc南京 K Kangaroo Puzzle

题意：有墙的空间，每个移动命令会被所有袋鼠执行，输出将所有袋鼠走到同一个格子上的操作（特判），上限50000。

思路：刚开始看完的思路是，就执行两个方向的操作到25000步，再反向执行25000步，因为步数很大，理论上袋鼠应该会走到一起，但总感觉有问题不敢写，后来学长说随机输出50000步就完事了，试了一下，果然a了。。。（后来看题解，因为空间大小只有20*20，所以状态数是有限的，每两只袋鼠走到一起最多只用80步，不可能超出50000步的上限，所以随机输出50000步即可。。。）

#include 
using namespace std;

int main(){
	int n,m;
	string s,k = "ULRD";
	scanf("%d%d",&n,&m);
	cin >> s;
	
	srand(time(0));
	for(int i = 0;i < 50000;++i) printf("%c",k[rand()%4]);
	return 0;
} 

**2018icpc徐州 A Rikka with Minimum Spanning Trees **

题意：求最小生成树权值和最小生成树种类的乘积

思路：
1.错误思路（想少了，但a掉了，原因后面会讲）：先用所有的边求一次最小生成树的权值，然后依次去掉最短边，看还能不能形成最小生成树，如果可以，那么种类加一。（实际上想错了，没考虑重边在后面的情况，只想了最小边的重边）

2.正确思路？（因为题目数据原因无法验证，且时间复杂度较高）：先求一遍最小生成树，再存权值重边，然后枚举权值重边lca找出的最小环里面有没有相同的权值边，每有一条种类就加一。

题解：因为题目边数最多为2e5条，且生成边权值的数据范围是ull，而生成的权值重边还恰好能和剩下的点生成最小生成树概率也很小，所以本题生成的最小生成树有两棵及以上的概率小的可以忽略不计，所以只用求一次最小生成树的权值即可

错误的ac代码

#include 
using namespace std;
typedef unsigned long long ull;
const ull mod = 1e9+7;

struct node{
	int u,v;
	ull w;
} e[100001];
ull k1,k2;
ull xorSFP(){
	ull k3 = k1,k4 = k2;
	k1 = k4;
	k3 ^= k3 << 23;
	k2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);
	return k2 + k4;
}

int n,m,pre[100001];

void init(int n){
	for(int i = 1;i <= n;++i) pre[i] = i;
	return ;
}

bool comp(node x,node y){
	return x.w < y.w;
}

int find(int x){
	return pre[x] = pre[x] == x ?x :find(pre[x]); 
}

ull kal(int i){
	ull sum = 0,cnt = 0;
	for(;i <= m;++i){
		if(cnt == n-1) break;
		int uu = find(e[i].u);
		int vv = find(e[i].v);
		if(uu != vv){
			pre[uu] = vv;
			sum = (sum + e[i].w) % mod;
			cnt++;
		}
	}
	return cnt == n-1 ?sum :0;
}

int main()
{
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%d%d%llu%llu",&n,&m,&k1,&k2);
		for(int i = 1;i <= m;++i){
			e[i].u = xorSFP() % n + 1;
			e[i].v = xorSFP() % n + 1;
			e[i].w = xorSFP();
		}
		sort(e+1,e+m+1,comp);
		
		init(n);
		ull temp,ans = 0,k = kal(1);
		if(k) ans += k;
		else{
			printf("0\n");
			continue;
		}
		
		for(int i = 2;i <= m;++i){
			temp = kal(i);
			if(temp == k) ans = (ans + k) % mod;
			else break;
		}
		printf("%llu\n",ans);
	}
	return 0;
}

5.变形图下的bfs

**2018icpc焦作 F Honeycomb **

题意：问蜜蜂从起点蜂房到终点蜂房所需要走的最小步数

思路：刚开始一直在想怎么用矩阵把蜂房表示出来（六边形），后来吴大佬说干嘛不直接存完整的图，仔细想想，完全有道理，然后存完图，确认六个方向的bfs，成功ac。（别用getline，太慢了，因为这个t了一次。。。）

#include 
using namespace std;

struct node{
	int x,y,s;
	node(int x,int y,int s):x(x),y(y),s(s){}
};

char mps[6000][6000];

int mvx[] = {-1,-1,-2,1,1,2};
int mvy[] = {-3,3,0,-3,3,0};

int bfs(int x,int y){
	queue <node> q;
	node u(x,y,1);
	q.push(u);
	
	while(!q.empty()){
		u = q.front();q.pop();
		for(int i = 0;i < 6;++i){
			int xx = u.x+mvx[i];
			int yy = u.y+mvy[i];
			int tx = xx+mvx[i];
			int ty = yy+mvy[i];
			if(mps[xx][yy] == ' '){
				if(mps[tx][ty] == 'T') return u.s+1;
				mps[xx][yy] = '*';
				node v(tx,ty,u.s+1);
				q.push(v);
			}
		}
	}
	return -1;
}

int main()
{
	int t;
	scanf("%d",&t);
	while(t--){
		int j,x,y,n,m;
		char k;
		scanf("%d%d",&n,&m);
		
		n = (n << 2) + 2;
		
		getchar();
		j = 0;
		for(int i = 0;i <= n;){
			k = getchar();
			if(k == '\n' || k == '\r'){
				mps[i][j] = '\0',j = 0,i++;
				continue;
			}
			if(k == 'S') x = i,y = j;
			mps[i][j] = k;
			j++;
		}
		
//		for(int i = 0;i <= n;++i){
//			printf("%s\n",mps[i]);
//		}
		
		printf("%d\n",bfs(x,y));
	}
	return 0;
}

6.打表思维题（打表找规律）

2018icpc北京 I Palindromes

题意：构造回文串。。。没了。。。

思路：打表找出了规律，然后emm 码了一遍代码 a掉（善用栈，朋友）

#include 
#include 
using namespace std;

stack <char> S;

int main()
{
//	freopen("test.in","r",stdin);
//
//	freopen("test.out","w",stdout);	

	int t;
	string s;
	scanf("%d",&t);
	while(t--){
		cin >> s;
		int len = s.size();
		if(len == 1) printf("%d\n",s[0] - '0' - 1);
		else if(len == 2 && s[0] == '1' && s[1] == '0') printf("9\n");
		else{
			string ans = "";
			if(s[0] == '1'){
				if(s[1] == '0'){
					ans += "9";
					S.push('9');
					for(int i = 2;i < len-1;++i) ans += s[i],S.push(s[i]);
					ans += s[len-1];
				}
				else{
					for(int i = 1;i < len;++i) ans += s[i],S.push(s[i]);
				}
			}
			else{
				ans += s[0] - 1;
				S.push(s[0] - 1);
				for(int i = 1;i < len-1;++i) ans += s[i],S.push(s[i]);
				ans += s[len-1];
			}
			cout << ans;
			while(!S.empty()) printf("%c",S.top()),S.pop();
			printf("\n");
		}
	}
	return 0;
}

**2018icpc北京 E Frog and Portal **

题意：200个荷叶，给青蛙设置传送门，保证青蛙有k种方法到达终点

思路：
错误思路：看出了是一个斐波那契数列，想着算差值，然后用两个数相加得到结果（最多只用两个传送门），但没法证明，并且这个差值该怎么算也有点无从下手

正确思路：后面想的时候，觉得之前对斐波那契的理解有点不深刻，后面的值既然是通过前面的值递推得到的，那么我完全可以设置传送门规定这一个位置到下一个位置是2的倍数还是就是一种走法，即分解为01串，二进制化

如果剩余步数为偶数：
x+1  ->  x+3
x+2  ->  x+3
如果剩余步数为奇数：
x+1  ->  199

上面是限制了x到x+3有两种走法还是一种走法，反正题目特判，用这种比较暴力的方式，
完全可以得到想要的结果，毕竟k最大才2^32

#include 
using namespace std;
typedef long long ll;

int u[2000000],v[2000000];

int main()
{
	ll m,cnt;
	while(~scanf("%lld",&m)){
		if(m == 0) printf("2\n1 1\n2 1\n");
		else if(m == 1) printf("2\n1 199\n2 2\n");
		else{
			int x = 0;
			cnt = 0;
			while(m > 2){
				if(m & 1){
					u[++cnt] = x+1,v[cnt] = 199;
					x = x+2;
					m -= 1;
				}
				else{
					u[++cnt] = x+1,v[cnt] = x+3;
					u[++cnt] = x+2,v[cnt] = x+3;
					x = x+3;
					m >>= 1;
				}
			}
			u[++cnt] = x+1,v[cnt] = 199;
			u[++cnt] = x+2,v[cnt] = 199;
			printf("%lld\n",cnt);
			for(int i = 1;i <= cnt;++i){
				printf("%d %d\n",u[i],v[i]);
			}
		}
	}
	return 0;
}