WaWa的奇妙冒险(第三周集训自闭现场)
第三周集训自闭现场(a* ida* dbfs真的好难)
- (一)wlacm例题记录
- A-有重复元素的排列问题 (水题,但卡我到自闭)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B-集合划分问题 (递推公式天下第一)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C-简单背包问题 (if的巧妙运用)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- D-双色Hanoi塔问题 (水题? ac的莫名其妙)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- E-蒜头君的生日 (基姆拉尔森计算公式)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- F-节假日 (水题,测试样例有问题)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- G-幼儿园买玩具 (水题,位运算枚举)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- H-蚂蚁感冒 (思维题,这个搜索不会写)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- I-最佳调度问题 (dfs的剪枝艺术)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- J-拆分自然数 (dfs)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- K-划分整数 (递推公式天下第一)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- L-素数环问题 (dfs)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- M-面积 (bfs)
- Sample Input
- Sample Output
- 理解
- AC代码
- N-最少转弯问题 (bfs)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (二)vjudge例题记录
- A-Shredding Company (水题,dfs切段)POJ - 1416
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- B-Sudoku (巧妙的标记法,dfs)POJ - 2676
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- C-Channel Allocation(四色定理天下第一)POJ - 1129
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- D-连连看 (dfs,剪枝很难,ac的莫名其妙)HDU - 1175
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- E-Black And White (dfs,巧妙的剪枝) HDU - 5113
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- F-Find The Multiple (dfs) POJ - 1426
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- G-Pots (bfs,模拟)POJ - 3414
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- H-Asteroids! (bfs) HDU - 1240
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- I-Friend Chains (bfs)HDU - 4460
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- J-Eight (a*,bfs)(POJ - 1077)
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- K-Solitaire (dbfs,模拟) HDU - 1401
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- L-Eight II (ida*) HDU - 3567
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- M-Power Calculus (ida*) POJ - 3134
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- N-DNA sequence (ida*)HDU - 1560
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- O-The Rotation Game (ida*,模拟) HDU - 1667
- Input
- Output
- Sample Input
- Sample Output
- 理解
- AC代码
- (三)一些收获
- 关于dfs
- 关于bfs
- 关于dbfs
- 关于a*算法
- 关于ida*
- (四)感想
(一)wlacm例题记录
A-有重复元素的排列问题 (水题,但卡我到自闭)
设R={ r1, r2 , …, rn}是要进行排列的n个元素。其中元素r1, r2 , …, rn可能相同。试设计一个算法,列出R的所有不同排列。
给定n 以及待排列的n 个元素。计算出这n 个元素的所有不同排列。
Input
输入数据的第1 行是元素个数n,1≤n≤500。接下来的1 行是待排列的n个元素。
Output
计算出的n个元素的所有不同排列并输出。文件最后1行中的数是排列总数。
Sample Input
4
aacc
Sample Output
aacc
acac
acca
caac
caca
ccaa
6
理解
说实话,第一眼看到这题目第一反应是写一个类似 next_permutation() 的函数,进行判重来决定换位还是不换位,但换完顺序真的还是有问题(
蒟蒻太菜了,真的没办法),后面换了一个思路,记录字母的数量,自己来拼串,这样就自动完成了去重,以及字典序升序的排序方式,虽然方法不那
么巧妙,但已经是蒟蒻的极限了
AC代码
#includeB-集合划分问题 (递推公式天下第一)
设S是一个具有n个元素的集合,S={a1,a2,……,an},现将S划分成k个满足下列条件的子集合S1,S2,……,Sk ,且满足:

则称S1,S2,……,Sk是集合S的一个划分。它相当于把S集合中的n个元素a1 ,a2,……,an 放入k个(0<k≤n<30)无标号的盒子中,使得没有一个盒子为空。请你确定n个元素a1 ,a2 ,……,an 放入k个无标号盒子中去的划分数S(n,k)。
Input
输入集合的元素个数n和划分的个数k
Output
输出划分数
Sample Input
23 7
Sample Output
4382641999117305
理解
看到这题第一眼,这和组合数好像(狗头),考虑缩减规模找递推公式
设k为划分集合数,n为元素数
当k = 1时,只能划分一个集合 return 1
当k = m时,只能划分成单个元素组成的集合 return 1
当k > m时,不能划分集合 return 0
接下来是缩减规模的方向,考虑(1)元素减1,划分数不变(2)元素减1,划分数减1
(下面是网上偷的一段,便于理解)
设n个元素的集合可以划分为F(n,k)个不同的由k个非空子集组成的集合。
考虑3个元素的集合,可划分为
① 1个子集的集合:{{1,2,3}}
② 2个子集的集合:{{1,2},{3}},{{1,3},{2}},{{2,3},{1}}
③ 3个子集的集合:{{1},{2},{3}}
∴F(3,1)=1;F(3,2)=3;F(3,3)=1;
如果要求F(4,2)该怎么办呢?
A.往①里添一个元素{4},得到{{1,2,3},{4}}
B.往②里的任意一个子集添一个4,得到
{{1,2,4},{3}},{{1,2},{3,4}},
{{1,3,4},{2}},{{1,3},{2,4}},
{{2,3,4},{1}},{{2,3},{1,4}}
∴F(4,2)=F(3,1)+2*F(3,2)=1+2*3=7
可以推得递推公式为 F(n,k) = F(n-1,k-1) + k*F(n-1,k)
后来学长也说了一下贝尔数,但有点看不懂,蒟蒻数学很差
原地址 https://blog.csdn.net/mikasa3/article/details/51283929
AC代码
#includeC-简单背包问题 (if的巧妙运用)
简单的背包问题。设有一个背包,可以放入的重量为s。现有n件物品,重量分别为w1,w2…,wn,(1≤i≤n)均为正整数,从n件物品中挑选若干件,使得放入背包的重量之和正好为s。找到一组解即可。
如果找不到,输出"not found"(引号不输出)
Input
第一行是物品总件数和背包的载重量,第二行为各物品的重量。
Output
各所选物品重量(按编号从小到大顺序输出)
Sample Input
5 10
1 2 3 4 5
Sample Output
number:1 weight:1
number:4 weight:4
number:5 weight:5
理解
刚开始做这题想用的是dp,只要看重量为s的背包里有没有重量的s的物品就好了,然而,他要求装了什么东西。。。瞬间自闭
之后的思路是洛谷 “选数” 的思路,取到了保存路径就ok,反正他只要一组,然后 wa33%
最后看完大佬代码,理解了一下,发现这道题取与不取(二叉树)写法之后,写了一个类似的,终于成功ac
其实看到二叉树本来是想开一个01数组去拼的(当时还没学位运算枚举),但发现大佬代码比这强很多,默默偷走(大佬牛逼)
AC代码
#include因为初学dfs,理解还很浅薄,这道题if的用法,感觉就像给当时的我开了新的大门,算是对dfs的搜索原理理解更深了一点吧
D-双色Hanoi塔问题 (水题? ac的莫名其妙)
设A、B、C是3 个塔座。开始时,在塔座A 上有一叠共n 个圆盘,这些圆盘自下而上,由大到小地叠在一起。各圆盘从小到大编号为1,2,……,n,奇数号圆盘着蓝色,偶数号圆盘着红色,如图所示。现要求将塔座A 上的这一叠圆盘移到塔座B 上,并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则(1):每次只能移动1 个圆盘;
规则(2):任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
规则(3):任何时刻都不允许将同色圆盘叠在一起;
规则(4):在满足移动规则(1)-(3)的前提下,可将圆盘移至A,B,C 中任一塔座上。
Input
输入正整数n。
Output
将计算出的最优移动方案输出。每一行由一个正整数k和2个字符c1和c2组成,表示将第k个圆盘从塔座c1移到塔座c2上。2个字符之间有1个空格。
Sample Input
3
Sample Output
1 A B
2 A C
1 B C
3 A B
1 C A
2 C B
1 A B
理解
当时真的没懂这题,因为单色汉诺塔都是懵懵懂懂的,姑且拿小规模的双色在纸上模拟了一遍,枚举到4发现,貌似和单色汉诺塔没啥不同
就大胆做了一个尝试,写了个单色汉诺塔的 a柱移b柱 发现就a掉了
AC代码
#includeE-蒜头君的生日 (基姆拉尔森计算公式)
蒜头君的生日快到了,蒜头君希望是在周末,蒜头君请你帮忙算出他生日在星期几。
Input
输入三个正整数,分别表示年、月、日。保证输入年份合法。
Output
输出星期几。用 Monday、Tuesday、Wednesday、Thursday、Friday、Saturday、Sunday 表示星期几。
Sample Input
1 1 1
Sample Output
Monday
理解
没啥好讲的,记录这题就是记录一下基姆拉尔森计算公式
W= (d+2*m+3*(m+1)/5+y+y/4-y/100+y/400+1)%7
在公式中d表示日期中的日数,m表示月份数,y表示年数。
注意:在公式中有个与其他公式不同的地方:
把一月和二月看成是上一年的十三月和十四月,例:如果是2004-1-10则换算成:2003-13-10来代入公式计算。
AC代码
#include F-节假日 (水题,测试样例有问题)
日历有阳历(公历)和阴历(农历)之分。每年都有法定节假日,这些分成三类——双休、阳历节假日、阴历节假日
1.双休
1)周六和周日2天
2.阳历节假日
1)元旦:阳历每年1月1日,放假1天
2)劳动节:阳历每年5月1日,放假1天
3)国庆节:阳历每年10月1日,放假3天
4)圣诞节:阳历每年12月25日,放假1天
3.阴历节假日
1)春节:阴历每年1月1日,放假3天
2)清明节:阳历每年4月4-6日之间的某天,放假1天
3)端午节:阴历每年5月5日,放假1天
4)中秋节:阴历每年8月15日,放假1天
当节假日和双休重合时,双休不延后也不提前,保证节假日之间不会重合。现在给你某年的所有阴历节假日的阳历日期,以及当年的1月1日是星期几,请你计算出这一年(阳历1月1日到12月31日)放了多少天假(包括双休、阳历节假日和阴历节假日)。
Input
第一行输入年份y(1900
最后一行一个整数表示当年1月1号是星期几(一周内的第几天,每周从星期一开始计数,即星期一为第一天)。
Output
输出一个整数,表示当年放假的天数。
Sample Input
2017
1 28
4 4
5 30
10 4
7
Sample Output
113
理解
思路是比较好像的,先统计一年里所有双休的天数,然后减去和双休重复的节假日就好了(基姆拉尔森计算公式)
但这题测试样例有问题,不符合实际,导致部分人疯狂wa
AC代码
#include G-幼儿园买玩具 (水题,位运算枚举)
蒜厂幼儿园有n个小朋友,每个小朋友都有自己想玩的玩具。身为幼儿园园长的你决定给幼儿园买一批玩具,由于经费有限,你只能买mm个玩具。已知玩具商店一共卖k种玩具,编号为1,2,3,…k,你让每个小朋友把想玩的玩具编号都写在了纸上。你希望满足尽可能多的小朋友的需求,请计算出最多能满足多少个小朋友的玩具需求
Input
第一行,输入三个整数n,m,k(1≤n≤100,1≤m≤k≤15),中间用空格分开
接下来n行,第i+1(0≤i
Output
输出一个整数,表示最多能满足多少小朋友的玩具需求。
Sample Input
5 3 5
2 1 4
0
2 3 1
3 2 3 4
2 4 5
Sample Output
3
理解
其实这题也是水题,但位运算讲的很浅,只讲了枚举这一块,姑且拿一道难一点的记录一下(其他比这个简单的多)
AC代码
#include H-蚂蚁感冒 (思维题,这个搜索不会写)
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左,有的朝右。 每只蚂蚁都只能沿着杆子向前爬,速度是1厘米/秒。当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
Input
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值,表示蚂蚁离开杆子左边端点的距离。正值表示头朝右,负值表示头朝左,数据中不会出现0值,也不会出现两只蚂蚁占用同一位置。其中,第一个数据代表的蚂蚁感冒了。
Output
要求输出1个整数,表示最后感冒蚂蚁的数目。
Sample Input
【测试样例1】
3
5 -2 8
【测试样例2】
5
-10 8 -20 12 25
Sample Output
【测试样例1】
1
【测试样例2】
3
理解
这题刚开始想着以为是搜索,发现完全想不到怎么搜索,然后找了一下规律,发现完全用不上搜索
以一个从左往右走的蚂蚁为例,他只有可能感染两个群体
(1)在他右边所有往左走的蚂蚁
(2)在他左边所有往右走的蚂蚁(注:需要他的右边有往左走的蚂蚁被感染才能出现第二个感染群体)
用左往右走也是类似情况,所以遍历两边就ac了
AC代码
#include I-最佳调度问题 (dfs的剪枝艺术)
假设有n个任务由k个可并行工作的机器完成。完成任务i需要的时间为ti。试设计一个算法找出完成这n个任务的最佳调度,使得完成全部任务的时间最早。
对任意给定的整数n和k,以及完成任务i需要的时间为ti,i=1~n。编程计算完成这n个任务的最佳调度。
Input
给出输入数据。第一行有2 个正整数n和k。第2 行的n个正整数是完成n个任务需要的时间。
Output
将计算出的完成全部任务的最早时间输出
Sample Input
7 3
2 14 4 16 6 5 3
Sample Output
17
理解
这道题是真的难,卡思路到死,后来问了大佬才知道怎么写,而且剪枝难度也是奇思妙想级别的(蒟蒻哭泣)
大概思路就是,先搜出第一种结果的值,用其来做一个min值来剪枝后面找到的结果
为了剪枝减的节点更高,先对所有的任务进行一个从大到小的排序,在进行dfs
AC代码
#include J-拆分自然数 (dfs)
任何一个大于1的自然数n,总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法:
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
Input
输入自然数n
Output
输出拆分的方案。
Sample Input
7
Sample Output
1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4
理解
刚开始这题写到心态爆炸,划分是简单的,但弄成字典升序是真的难
后面想到的思路类似拆分的写法加上最后的数字应当大于等于之前的数字,完成了ac
AC代码
#include K-划分整数 (递推公式天下第一)
将整数n分成k份,且每份不能为空,任意两种分法不能相同(不考虑顺序)。例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。
Input
输入n,k (6 输出一个整数,即不同的分法。 7 3 4 素数环:从1到n(1<=n<=12)这n个数摆成一个环,要求相邻的两个数的和是一个素数。 请输出最多前5个答案以及方案总数。 如果无解,输出"no solution!"(引号不输出) 输入n 请输出最多前5个答案(不足5个按实际答案数输出) 以及方案总数。 如果无解,输出"no solution!"(引号不输出) 10 <1>1 2 3 4 7 6 5 8 9 10 编程计算由“”号围成的下列图形的面积。面积计算方法是统计号所围成的闭合曲线中水平线和垂直线交点的数目。如下图所示,在1010的二维数组中,有“”围住了15个点,因此面积为15。 0 0 0 0 0 0 0 0 0 0 0 0 0 0 * * * 0 0 0 0 0 0 0 * 0 0 * 0 0 0 0 0 0 0 * 0 0 * 0 0 0 * 0 0 0 * 0 * 0 0 * 0 * 0 * 0 0 * 0 0 * 0 0 * * 0 * * 0 0 0 * 0 0 0 0 * 0 0 0 0 0 * * * * * 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 15 给出一张地图,这张地图被分为n×m(n,m<=100)个方块,任何一个方块不是平地就是高山。平地可以通过,高山则不能。现在你处在地图的(x1,y1)这块平地,问:你至少需要拐几个弯才能到达目的地(x2,y2)?你只能沿着水平和垂直方向的平地上行进,拐弯次数就等于行进方向的改变(从水平到垂直或从垂直到水平)的次数。例如:如图,最少的拐弯次数为5。 第1行:n m 第2至n+1行:整个地图地形描述(0:空地;1:高山), 如(图)第2行地形描述为:1 0 0 0 0 1 0 第n+2行:x1 y1 x2 y2 (分别为起点、终点坐标) 输出s (即最少的拐弯次数) 5 7 5 第一种想法,记录转弯次数和方向 第二种写法(这种肯定对的) You have just been put in charge of developing a new shredder for the Shredding Company Although a “normal” shredder would just shred sheets of paper into little pieces so that the contents would become unreadable, this new shredder needs to have the following unusual basic characteristics. 1.The shredder takes as input a target number and a sheet of paper with a number written on it. 2.It shreds (or cuts) the sheet into pieces each of which has one or more digits on it. 3.The sum of the numbers written on each piece is the closest possible number to the target number, without going over it. For example, suppose that the target number is 50, and the sheet of paper has the number 12346. The shredder would cut the sheet into four pieces, where one piece has 1, another has 2, the third has 34, and the fourth has 6. This is because their sum 43 (= 1 + 2 + 34 + 6) is closest to the target number 50 of all possible combinations without going over 50. For example, a combination where the pieces are 1, 23, 4, and 6 is not valid, because the sum of this combination 34 (= 1 + 23 + 4 + 6) is less than the above combination’s 43. The combination of 12, 34, and 6 is not valid either, because the sum 52 (= 12 + 34 + 6) is greater than the target number of 50. There are also three special rules : 1.If the target number is the same as the number on the sheet of paper, then the paper is not cut. For example, if the target number is 100 and the number on the sheet of paper is also 100, then the paper is not cut. 2.If it is not possible to make any combination whose sum is less than or equal to the target number, then error is printed on a display. For example, if the target number is 1 and the number on the sheet of paper is 123, it is not possible to make any valid combination, as the combination with the smallest possible sum is 1, 2, 3. The sum for this combination is 6, which is greater than the target number, and thus error is printed. 3.If there is more than one possible combination where the sum is closest to the target number without going over it, then rejected is printed on a display. For example, if the target number is 15, and the number on the sheet of paper is 111, then there are two possible combinations with the highest possible sum of 12: (a) 1 and 11 and (b) 11 and 1; thus rejected is printed. In order to develop such a shredder, you have decided to first make a simple program that would simulate the above characteristics and rules. Given two numbers, where the first is the target number and the second is the number on the sheet of paper to be shredded, you need to figure out how the shredder should “cut up” the second number. The input consists of several test cases, each on one line, as follows : tl num1 Each test case consists of the following two positive integers, which are separated by one space : (1) the first integer (ti above) is the target number, (2) the second integer (numi above) is the number that is on the paper to be shredded. Neither integers may have a 0 as the first digit, e.g., 123 is allowed but 0123 is not. You may assume that both integers are at most 6 digits in length. A line consisting of two zeros signals the end of the input. For each test case in the input, the corresponding output takes one of the following three types : sum part1 part2 … In the first type, partj and sum have the following meaning : 1.Each partj is a number on one piece of shredded paper. The order of partj corresponds to the order of the original digits on the sheet of paper. 2.sum is the sum of the numbers after being shredded, i.e., sum = part1 + part2 +… Each number should be separated by one space. 50 12346 43 1 2 34 6 Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task. The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0. For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them. 1 143628579 When a radio station is broadcasting over a very large area, repeaters are used to retransmit the signal so that every receiver has a strong signal. However, the channels used by each repeater must be carefully chosen so that nearby repeaters do not interfere with one another. This condition is satisfied if adjacent repeaters use different channels. Since the radio frequency spectrum is a precious resource, the number of channels required by a given network of repeaters should be minimised. You have to write a program that reads in a description of a repeater network and determines the minimum number of channels required. 如果找不到,输出"not found"(引号不输出) The input consists of a number of maps of repeater networks. Each map begins with a line containing the number of repeaters. This is between 1 and 26, and the repeaters are referred to by consecutive upper-case letters of the alphabet starting with A. For example, ten repeaters would have the names A,B,C,…,I and J. A network with zero repeaters indicates the end of input. Following the number of repeaters is a list of adjacency relationships. Each line has the form: A:BCDH which indicates that the repeaters B, C, D and H are adjacent to the repeater A. The first line describes those adjacent to repeater A, the second those adjacent to B, and so on for all of the repeaters. If a repeater is not adjacent to any other, its line has the form A: The repeaters are listed in alphabetical order. Note that the adjacency is a symmetric relationship; if A is adjacent to B, then B is necessarily adjacent to A. Also, since the repeaters lie in a plane, the graph formed by connecting adjacent repeaters does not have any line segments that cross. For each map (except the final one with no repeaters), print a line containing the minumum number of channels needed so that no adjacent channels interfere. The sample output shows the format of this line. Take care that channels is in the singular form when only one channel is required. 2 1 channel needed. “连连看”相信很多人都玩过。没玩过也没关系,下面我给大家介绍一下游戏规则:在一个棋盘中,放了很多的棋子。如果某两个相同的棋子,可以通过一条线连起来(这条线不能经过其它棋子),而且线的转折次数不超过两次,那么这两个棋子就可以在棋盘上消去。不好意思,由于我以前没有玩过连连看,咨询了同学的意见,连线不能从外面绕过去的,但事实上这是错的。现在已经酿成大祸,就只能将错就错了,连线不能从外围绕过。 输入数据有多组。每组数据的第一行有两个正整数n,m(0 每一组输入数据对应一行输出。如果能消去则输出"YES",不能则输出"NO"。 3 4 YES In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. In this problem, you have to solve the 4-color problem. Hey, I’m just joking. You are asked to solve a similar problem: Color an N × M chessboard with K colors numbered from 1 to K such that no two adjacent cells have the same color (two cells are adjacent if they share an edge). The i-th color should be used in exactly c i cells. Matt hopes you can tell him a possible coloring. The first line contains only one integer T (1 ≤ T ≤ 5000), which indicates the number of test cases. For each test case, the first line contains three integers: N, M, K (0 < N, M ≤ 5, 0 < K ≤ N × M ). The second line contains K integers c i (c i > 0), denoting the number of cells where the i-th color should be used. It’s guaranteed that c 1 + c 2 + · · · + c K = N × M . For each test case, the first line contains “Case #x:”, where x is the case number (starting from 1). In the second line, output “NO” if there is no coloring satisfying the requirements. Otherwise, output “YES” in one line. Each of the following N lines contains M numbers seperated by single whitespace, denoting the color of the cells. If there are multiple solutions, output any of them. 4 Case #1: Given a positive integer n, write a program to find out a nonzero multiple m of n whose decimal representation contains only the digits 0 and 1. You may assume that n is not greater than 200 and there is a corresponding m containing no more than 100 decimal digits. The input file may contain multiple test cases. Each line contains a value of n (1 <= n <= 200). A line containing a zero terminates the input. For each value of n in the input print a line containing the corresponding value of m. The decimal representation of m must not contain more than 100 digits. If there are multiple solutions for a given value of n, any one of them is acceptable. 2 10 我tle的bfs 后来学长提到了中国剩余定理(孙子问题)的解题方式,不过还没看(蒟蒻写题到自闭1555) You are given two pots, having the volume of A and B liters respectively. The following operations can be performed: 1.FILL(i) fill the pot i (1 ≤ i ≤ 2) from the tap; Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots. On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B). The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’. 3 5 4 6 You’re in space. Input to this problem will consist of a (non-empty) series of up to 100 data sets. Each data set will be formatted according to the following description, and there will be no blank lines separating data sets. A single data set has 5 components: Start line - A single line, “START N”, where 1 <= N <= 10. Slice list - A series of N slices. Each slice is an N x N matrix representing a horizontal slice through the asteroid field. Each position in the matrix will be one of two values: ‘O’ - (the letter “oh”) Empty space ‘X’ - (upper-case) Asteroid present Starting Position - A single line, “A B C”, denoting the Target Position - A single line, “D E F”, denoting the End line - A single line, “END” The origin of the coordinate system is <0,0,0>. Therefore, each component of each coordinate vector will be an integer between 0 and N-1, inclusive. The first coordinate in a set indicates the column. Left column = 0. The second coordinate in a set indicates the row. Top row = 0. The third coordinate in a set indicates the slice. First slice = 0. Both the Starting Position and the Target Position will be in empty space. For each data set, there will be exactly one output set, and there will be no blank lines separating output sets. A single output set consists of a single line. If a route exists, the line will be in the format “X Y”, where X is the same as N from the corresponding input data set and Y is the least number of moves necessary to get your ship from the starting position to the target position. If there is no route from the starting position to the target position, the line will be “NO ROUTE” instead. A move can only be in one of the six basic directions: up, down, left, right, forward, back. Phrased more precisely, a move will either increment or decrement a single component of your current position vector by 1. START 1 1 0 For a group of people, there is an idea that everyone is equals to or less than 6 steps away from any other person in the group, by way of introduction. So that a chain of “a friend of a friend” can be made to connect any 2 persons and it contains no more than 7 persons. There are multiple cases. For each case, print the minimum value k in one line. 3 2 The 15-puzzle has been around for over 100 years; even if you don’t know it by that name, you’ve seen it. It is constructed with 15 sliding tiles, each with a number from 1 to 15 on it, and all packed into a 4 by 4 frame with one tile missing. Let’s call the missing tile ‘x’; the object of the puzzle is to arrange the tiles so that they are ordered as: 5 6 7 8 9 10 11 12 13 14 15 x where the only legal operation is to exchange ‘x’ with one of the tiles with which it shares an edge. As an example, the following sequence of moves solves a slightly scrambled puzzle: 5 6 7 8 5 6 7 8 5 6 7 8 5 6 7 8 9 x 10 12 9 10 x 12 9 10 11 12 9 10 11 12 13 14 11 15 13 14 11 15 13 14 x 15 13 14 15 x The letters in the previous row indicate which neighbor of the ‘x’ tile is swapped with the ‘x’ tile at each step; legal values are ‘r’,‘l’,‘u’ and ‘d’, for right, left, up, and down, respectively. Not all puzzles can be solved; in 1870, a man named Sam Loyd was famous for distributing an unsolvable version of the puzzle, and In this problem, you will write a program for solving the less well-known 8-puzzle, composed of tiles on a three by three You will receive a description of a configuration of the 8 puzzle. The description is just a list of the tiles in their initial positions, with the rows listed from top to bottom, and the tiles listed from left to right within a row, where the tiles are represented by numbers 1 to 8, plus ‘x’. For example, this puzzle x 4 6 7 5 8 is described by this list: 1 2 3 x 4 6 7 5 8 You will print to standard output either the word ``unsolvable’’, if the puzzle has no solution, or a string consisting entirely of the letters ‘r’, ‘l’, ‘u’ and ‘d’ that describes a series of moves that produce a solution. The string should include no spaces and start at the beginning of the line. 2 3 4 1 5 x 7 6 8 ullddrurdllurdruldr Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively. There are four identical pieces on the board. In one move it is allowed to: move a piece to an empty neighboring field (up, down, left or right), jump over one neighboring piece to an empty field (up, down, left or right). There are 4 moves allowed for each piece in the configuration shown above. As an example let’s consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right. Write a program that: reads two chessboard configurations from the standard input, verifies whether the second one is reachable from the first one in at most 8 moves, writes the result to the standard output. Each of two input lines contains 8 integers a1, a2, …, a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file. The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise. 4 4 4 5 5 4 6 5 YES Eight-puzzle, which is also called “Nine grids”, comes from an old game. In this game, you are given a 3 by 3 board and 8 tiles. The tiles are numbered from 1 to 8 and each covers a grid. As you see, there is a blank grid which can be represented as an ‘X’. Tiles in grids having a common edge with the blank grid can be moved into that blank grid. This operation leads to an exchange of ‘X’ with one tile. We use the symbol ‘r’ to represent exchanging ‘X’ with the tile on its right side, and ‘l’ for the left side, ‘u’ for the one above it, ‘d’ for the one below it. The first line is T (T <= 200), which means the number of test cases of this problem. The input of each test case consists of two lines with state A occupying the first line and state B on the second line. For each test case two lines are expected. The first line is in the format of “Case x: d”, in which x is the case number counted from one, d is the minimum length of operation list you need to turn A to B. 2 Case 1: 2 Starting with x and repeatedly multiplying by x, we can compute x31 with thirty multiplications: x2 = x × x, x3 = x2 × x, x4 = x3 × x, …, x31 = x30 × x. The operation of squaring can be appreciably shorten the sequence of multiplications. The following is a way to compute x31 with eight multiplications: x2 = x × x, x3 = x2 × x, x6 = x3 × x3, x7 = x6 × x, x14 = x7 × x7, x15 = x14 × x, x30 = x15 × x15, x31 = x30 × x. This is not the shortest sequence of multiplications to compute x31. There are many ways with only seven multiplications. The following is one of them: x2 = x × x, x4 = x2 × x2, x8 = x4 × x4, x8 = x4 × x4, x10 = x8 × x2, x20 = x10 × x10, x30 = x20 × x10, x31 = x30 × x. If division is also available, we can find a even shorter sequence of operations. It is possible to compute x31 with six operations (five multiplications and one division): x2 = x × x, x4 = x2 × x2, x8 = x4 × x4, x16 = x8 × x8, x32 = x16 × x16, x31 = x32 ÷ x. This is one of the most efficient ways to compute x31 if a division is as fast as a multiplication. Your mission is to write a program to find the least number of operations to compute xn by multiplication and division starting with x for the given positive integer n. Products and quotients appearing in the sequence should be x to a positive integer’s power. In others words, x−3, for example, should never appear. The input is a sequence of one or more lines each containing a single integer n. n is positive and less than or equal to 1000. The end of the input is indicated by a zero. Your program should print the least total number of multiplications and divisions required to compute xn starting with x for the integer n. The numbers should be written each in a separate line without any superfluous characters such as leading or trailing spaces. 1 0 The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it. For example, given “ACGT”,“ATGC”,“CGTT” and “CAGT”, you can make a sequence in the following way. It is the shortest but may be not the only one. The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5. For each test case, print a line containing the length of the shortest sequence that can be made from these sequences. 1 8 The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind. Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration. The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0’ after the last test case that ends the input. For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from 1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 AC dfs的学习可能是因为是一些比较基础的内容,所以压力还没有那么大(后面那些魔鬼剪枝当我没说),实际上目前看到的大部分dfs还是和回溯结合进行操作的,在一些特殊情况下会不用回溯,下面总结了一些可能用到dfs的题型 题目要求的东西可能是多重要求的总和,重点还是得看题目要求,选择适当的方法进行处理 如果说dfs是类似于树搜到低然后再返回,bfs就是树一层层节点遍历过去,用铺天盖地的方式找出结果,但因为不用一次次搜到底再返回,在一些题目上有显著的优势,一些可能用到bfs的题型 对dbfs说实话感触不深,毕竟只写了一题 “Solitaire” ,但大概还是知道怎么写了,根据bfs大面积铺地毯式的操作方式,dbfs确实是减少了铺地毯的面积,以后希望还可以遇到类似题目再练练(其实 “Eight II ”)完全可以拿来练dbfs来着,就是真的太忙了,之前的题都没空补。。。 唯一写的几题,都是套了曼哈顿距离的启发函数,感触还不是很深,但大概理解了他的运作方式,我们可以用走迷宫的方式理解bfs,先来后到的公平原则使他能按步数均匀地铺地毯 而加上a的bfs则改变了铺地毯的方式,他会选择最能接近目标的地方有限铺地毯,实际上用a算法的bfs就是自己定义了一个优先级,改变原先得公平原则(可以用优先队列实现) 启发函数是灵魂,好的启发函数才能完成优秀的bfs “剪枝” ida*实际上就是在无法预测深度的情况下,自行设立深度,以防止搜索深度过深tle,或者广度过广mle,虽然会重复小规模dfs,但比起不知深度的无限搜索优化了特别多 关键也是启发函数,用来确定是不是已经到不了终点了,及时停止dfs以继续扩大预期值 这个星期也算是在dfs和bfs上面入了一个门,对于简单的dfs和bfs题目已经能做做看了,需要剪枝的也能做出尝试,感觉一些过去学的东西貌似在这一周也给了我很多帮助 1.上周写的模拟确实是对有了一个不错的帮助,因为脑子可以模拟比较简单的dfs和bfs搜索过程了,对于两者的理解也是更深了,而写一些模拟类操作时,感觉压力也已经小了很多 2.曾经看的链表(虽然只看了单向链表),确实是对理解dfs是有帮助的,而且帮助还不小,至少你在知道树这个结构和栈的前提下,理解dfs就是另一回事了,和当初刚学递归时一脸懵逼的状况相比好了很多,至少有基础垫一下了 3.开始能在递归里面找错,具体方式就是锁定区域,重新思考(看中间量确实十分有用) 当然还是有非常多的不做 1.自己写的时候,一些难一点的剪枝还是构架不起来,对这一块的能力还是比较弱 2.对于更进一步的a* ida* dbfs写的题目还是太少了,只是懂了,但运用方面问题还是很大,在看完别人题解之后虽然能写大体,但细节上操作起来还是比较差 总结来说,这一周学的勉强还算可以,至少对dfs和bfs的入门是学了不少,关于后面更进一步的搜索算法之类的,之后再继续努力吧,这个暑假还是得兼顾广度 (革命尚未成功,同志尚需努力[狗头])Output
Sample Input
Sample Output
理解
看到题目第一反应,又是一个递推公式,莫名想到当初写的 “分梨” 【狗头】
这道题大概也能看做没有空盘的分梨
所以大概思路就比较好理了
k = 1,return 1
n = k,return 1
k > n,return 0
因为当做分梨来看,我们可以缩小两个方向的规模
F(n-1,k-1) 因为少一个盘子和一个梨,只要把梨加到多出来的空盘子里就好了
F(n-k,k) 盘子没少,但少了梨,因为你不能出现重复的组合,所以你要把每盘都加一个梨,不改变原状态
得到公式F(n,k) = F(n-1,k-1) + F(n-k,k)
AC代码
#include L-素数环问题 (dfs)
Input
Output
Sample Input
Sample Output
<2>1 2 3 4 7 10 9 8 5 6
<3>1 2 3 4 9 8 5 6 7 10
<4>1 2 3 8 5 6 7 4 9 10
<5>1 2 3 8 5 6 7 10 9 4
960理解
一道中规中矩的dfs题目,剪枝也不难,但没全局变量的初始化卡了一年(貌似oj无视了全局变量里面的初始化导致我一直wa)
大体思路:
(1)打表判断两数和是否为素数
(2)奇数全部剪枝(1除外),因为奇数情况下必然有两个奇数相连,而素数里面只有2为偶数
其他的dfs搜就完事了
AC代码
#include M-面积 (bfs)
Sample Input
0 0 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 0 1 0
0 1 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0Sample Output
理解
这道题也是不难,之前因为bfs和dfs没学且不熟,在上一周真写不了这个的搜索
这周写这题就很轻松了,大概思路就是把外层的0涂成1,然后统计剩下的0的数量
不过要注意开始涂色的坐标,为了防止外圈1,我的思路是在外面再包一层0
AC代码
#include N-最少转弯问题 (bfs)
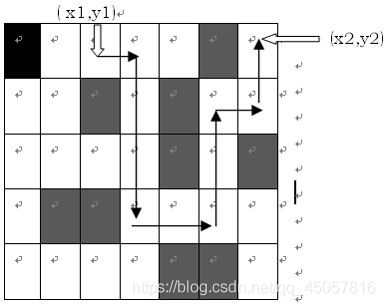
Input
第3行地形描述为:0 0 1 0 1 0 0
……
Output
Sample Input
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7Sample Output
理解
在做这道题之前,我是已经码了一遍vj上的连连看,所以最开始的思路就是推步数,记录方向,当方向不同时记录拐弯次数(刚开始当做-1处理,且其
不存在回头这种操作,所以我们可以用i直接当方向使用)
使用这个想法时也进行了思考,拐弯次数多的情况下,其步数(默认先进的先出,有一个步数的效果)必然比拐弯次数少的情况来的大(个人想法,不
确定)
这个想法是成功ac了,但学长貌似说样例设置不太好,没有考虑最小值情况直接输出第一个找到的就能ac?
所以后面看了大佬的代码,写了第二个思路的写法,记录拐弯次数,按拐弯次数的递增构架bfs,这种思路应该是能解决找最小值的问题的,也ac了
AC代码
#include #include (二)vjudge例题记录
A-Shredding Company (水题,dfs切段)POJ - 1416

Figure 1. Shredding a sheet of paper having the number 12346 when the target number is 50Input
t2 num2
…
tn numn
0 0Output
rejected
error
The message error is printed if it is not possible to make any combination, and rejected if there is
more than one possible combination.
No extra characters including spaces are allowed at the beginning of each line, nor at the end of each line.Sample Input
376 144139
927438 927438
18 3312
9 3142
25 1299
111 33333
103 862150
6 1104
0 0Sample Output
283 144 139
927438 927438
18 3 3 12
error
21 1 2 9 9
rejected
103 86 2 15 0
rejected理解
也是一道比较简单的dfs,写的时候顺手就剪枝了,所以没感到啥压力
题目大意:
分割纸上的数字,找出他们加起来小于等于之前输入值的最大值
AC代码
#include B-Sudoku (巧妙的标记法,dfs)POJ - 2676

Input
Output
Sample Input
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107Sample Output
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127理解
这道题实际上N皇后区别不大,就是判断该行、该列、该小格里的某个数字是否已经被使用过
行和列的判断及其简单,这个不必说了
小格的判断则可以套用一个很神奇的公式map[i/3*3 + y/3][x]
在棋盘的涵盖范围为(0,0)到(8.8)时,可以正好得到9小格的范围
AC代码
#include C-Channel Allocation(四色定理天下第一)POJ - 1129
Input
Output
Sample Input
A:
B:
4
A:BC
B:ACD
C:ABD
D:BC
4
A:BCD
B:ACD
C:ABD
D:ABC
0Sample Output
3 channels needed.
4 channels needed.理解
大意,相邻的信号塔不能用同一种中继器,题中会告诉你哪些塔是相邻的
看到这题第一反应是分集合,相邻的别分到一起就行了,后面想想实现起来很难
换了个思维,相邻的信号塔不能涂同一种颜色就ok了
因为先写的 “Black And White” 这一题,对四色问题有了了解(再上一次看见就是在《嫌疑人X的献身
》里了,当时跑去查过四色问题)
因为四色定理,颜色最多就四种,一定意义上完成了很大幅度的剪枝
AC代码
#include D-连连看 (dfs,剪枝很难,ac的莫名其妙)HDU - 1175
玩家鼠标先后点击两块棋子,试图将他们消去,然后游戏的后台判断这两个方格能不能消去。现在你的任务就是写这个后台程序。Input
Output
Sample Input
1 2 3 4
0 0 0 0
4 3 2 1
4
1 1 3 4
1 1 2 4
1 1 3 3
2 1 2 4
3 4
0 1 4 3
0 2 4 1
0 0 0 0
2
1 1 2 4
1 3 2 3
0 0Sample Output
NO
NO
NO
NO
YES理解
一道比较有意思的dfs,剪枝起来有难度
大意:问你这两块能不能通过连连看的方式消除掉,有以下几个条件
(1)线段只能转弯两次
(2)线段不能从外面绕过去
关于转弯两次可以用可以用记方向的方式解决,因为不可能往回走,所以当i发生变化时,方向必然已经发
生了变化,且当两次转弯后,他只能往最后的方向一直走下去,看能不能到达终点
这道题真的a的莫名其妙,剪枝的调节没怎么改,改着改着emm 就过了? 貌似多了一个回溯来着,本来想
着找一条路就ok,不用写回溯来着。。。
AC代码
#include E-Black And White (dfs,巧妙的剪枝) HDU - 5113
— Wikipedia, the free encyclopediaInput
Output
Sample Input
1 5 2
4 1
3 3 4
1 2 2 4
2 3 3
2 2 2
3 2 3
2 2 2Sample Output
NO
Case #2:
YES
4 3 4
2 1 2
4 3 4
Case #3:
YES
1 2 3
2 3 1
Case #4:
YES
1 2
2 3
3 1理解
题目是很好理解的,就是问你M*N的棋盘能不能用K种颜色(每种颜色有数量限制)涂满且无相同颜色相邻
单纯写这题是很简单的,考虑一个取色就好了,但剪枝有点难,tle到爆炸后看了大佬代码才懂怎么剪枝
下面假设一个3*3的棋盘
只有两种涂色,我们可以发现,当一种颜色超过它一半棋盘的格数+1的时候,已经做不到相邻格子涂色不
同了,以此类推,得到公式 color[i] > (n*m - sum + 1)/2)时进行剪枝
AC代码
#include F-Find The Multiple (dfs) POJ - 1426
Input
Output
Sample Input
6
19
0Sample Output
100100100100100100
111111111111111111理解
思路是比较好想的,找个能整除6的就行,根据取模运算
刚开始自己写了bfs,然而疯狂tle???
然后看了学长讲了dfs的写法,才会写,但还是没懂bfs为啥就tle了
AC代码
#include #include G-Pots (bfs,模拟)POJ - 3414
2.DROP(i) empty the pot i to the drain;
3.POUR(i,j) pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).Input
Output
Sample Input
Sample Output
FILL(2)
POUR(2,1)
DROP(1)
POUR(2,1)
FILL(2)
POUR(2,1)理解
题目很好理解,两个壶相互倒以及加水和倒水的操作,使其中一个壶内的水达到要求要求的水量即可
个人理解过来,就是把我们之前写的类似迷宫的写法(4种操作方式)改成题目中的六种操作即可
因为上周写的大量的模拟题,这种题目的模拟写起来还是很简单的
AC代码
#include H-Asteroids! (bfs) HDU - 1240
You want to get home.
There are asteroids.
You don’t want to hit them.Input
Output
Sample Input
O
0 0 0
0 0 0
END
START 3
XXX
XXX
XXX
OOO
OOO
OOO
XXX
XXX
XXX
0 0 1
2 2 1
END
START 5
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
XXXXX
XXXXX
XXXXX
XXXXX
XXXXX
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
OOOOO
0 0 0
4 4 4
ENDSample Output
3 4
NO ROUTE理解
题意也是很简单的,大意就是走三维迷宫,唯一要注意的点是,因为迷宫是三维的,在填入时,要把z轴放
在最外层(z轴增加最慢)
AC代码
#include I-Friend Chains (bfs)HDU - 4460
For example, if XXX is YYY’s friend and YYY is ZZZ’s friend, but XXX is not ZZZ’s friend, then there is a friend chain of length 2 between XXX and ZZZ. The length of a friend chain is one less than the number of persons in the chain.
Note that if XXX is YYY’s friend, then YYY is XXX’s friend. Give the group of people and the friend relationship between them. You want to know the minimum value k, which for any two persons in the group, there is a friend chain connecting them and the chain’s length is no more than k .Input
For each case, there is an integer N (2<= N <= 1000) which represents the number of people in the group.
Each of the next N lines contains a string which represents the name of one people. The string consists of alphabet letters and the length of it is no more than 10.
Then there is a number M (0<= M <= 10000) which represents the number of friend relationships in the group.
Each of the next M lines contains two names which are separated by a space ,and they are friends.
Input ends with N = 0.Output
If the value of k is infinite, then print -1 instead.Sample Input
XXX
YYY
ZZZ
2
XXX YYY
YYY ZZZ
0Sample Output
理解
题目大意是,找出最长的朋友链,我和这人之间隔了多少人,朋友链长度就是隔的人数加1,如果出现没法
联系的朋友,就输出-1
AC代码
#include J-Eight (a*,bfs)(POJ - 1077)
1 2 3 4
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 r-> d-> r->
frustrating many people. In fact, all you have to do to make a regular puzzle into an unsolvable one is to swap two tiles (not counting the missing ‘x’ tile, of course).
arrangement.Input
1 2 3Output
Sample Input
Sample Output
理解
把输入的八数码转成12345678x要多少步,输出最短步数的走法(可能有多种)
刚开始写的朴素的bfs,结构体里面保存路径,直接mle
后来反向打了一个表,想着只有362880种可能性,但还是tle
无奈看了大佬的a*算法,才a了这题
AC代码
#include K-Solitaire (dbfs,模拟) HDU - 1401
Input
Output
Sample Input
2 4 3 3 3 6 4 6Sample Output
理解
大意就是按他的要求把棋子走到相应的位置即可(8步以内)
书上说了可以用dbfs写(也没怎么说怎么从起点和结尾同时开始搜索)
刚开始写的时候开了一个vis[8][8][8][8][8][8][8][8]标记状态,然后用1和2来记录是起点走的还是终
点走的,且开了两个队列
后面发现写出了 “灵异事件” ,起点第一个棋子走完第一步之后,终点第一个棋子会走第一步,然后回来
继续起点棋子走一步。。。而且没有输出
咋改都改不出来,后来看来大佬的写法,写成一个队列之后成功ac
AC代码
#include L-Eight II (ida*) HDU - 3567

A state of the board can be represented by a string S using the rule showed below.

The problem is to operate an operation list of ‘r’, ‘u’, ‘l’, ‘d’ to turn the state of the board from state A to state B. You are required to find the result which meets the following constrains:
Input
It is guaranteed that there is an available solution from state A to B.Output
S is the operation list meeting the constraints and it should be showed on the second line.Sample Input
12X453786
12345678X
564178X23
7568X4123Sample Output
dd
Case 2: 8
urrulldr理解
找出最小字典序的路径的串
拿刚学的a*写了一遍,发现调整不了输出路径的字典序,瞬间自闭
dbfs也不会写,想不通该咋做到字典序最小(起点从小到大,终点从大到小?)
最后学了大佬一手ida*,成功a题
AC代码
#include M-Power Calculus (ida*) POJ - 3134
Input
Output
Sample Input
31
70
91
473
512
811
953
0Sample Output
6
8
9
11
9
13
12理解
书上也讲的很明白了,当成n的加减法,自己判断深度够不够,不够就继续加
AC代码
#include N-DNA sequence (ida*)HDU - 1560

Input
Output
Sample Input
4
ACGT
ATGC
CGTT
CAGTSample Output
理解
大意也是比较简单,自己创造一个最短的串,能把给的串通过相同相消的方式消除干净就行
每次dfs枚举4^n个串就好,n为深度
AC代码
#include O-The Rotation Game (ida*,模拟) HDU - 1667

Input
Output
A' toH’, and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed’ instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases.Sample Input
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0Sample Output
2
DDHH
2理解
题意理解起来不难,通过八种操作,使中间的八个数字相等即可
用ida*很简单就可以a掉
AC代码
#include (三)一些收获
关于dfs
1.判断这条路是否能走通(触底反弹到找到一条即可)
2.输出最小字典序的答案或者按字典序输出所有能找到的答案
3.判断有多少种可能性
4.找出最小值或者最大值
关于bfs
1.判断这条路是否能走通(触底反弹到找到一条即可)
2.找出最小值或者最大值(特殊情况可以用,具体看题目)
3.最短步数或者最小拐弯数
关于dbfs
关于a*算法
关于ida*
(四)感想

