LeetCode第200场周赛Java双百解法

1534. 统计好三元组

给你一个整数数组 arr ，以及 a、b 、c 三个整数。请你统计其中好三元组的数量。

如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件，则认为它是一个 好三元组 。

0 <= i < j < k < arr.length
|arr[i] - arr[j]| <= a
|arr[j] - arr[k]| <= b
|arr[i] - arr[k]| <= c
其中 |x| 表示 x 的绝对值。

返回 好三元组的数量 。

分析 水题，数组长度极小，可直接三次循环解答。

class Solution {
    public int getAbs(int n){
        return Math.abs(n);
    }
    public int countGoodTriplets(int[] arr, int a, int b, int c) {
        int ans=0,len=arr.length;
        for(int i=0;i<len;i++){
            for(int j=i+1;j<len;j++){
                for(int k=j+1;k<len;k++){
                    if(getAbs(arr[i]-arr[j])<=a&&getAbs(arr[j]-arr[k])<=b&&getAbs(arr[i]-arr[k])<=c)
                        ans++;
                }
            }
        }
        return ans;
    }
}

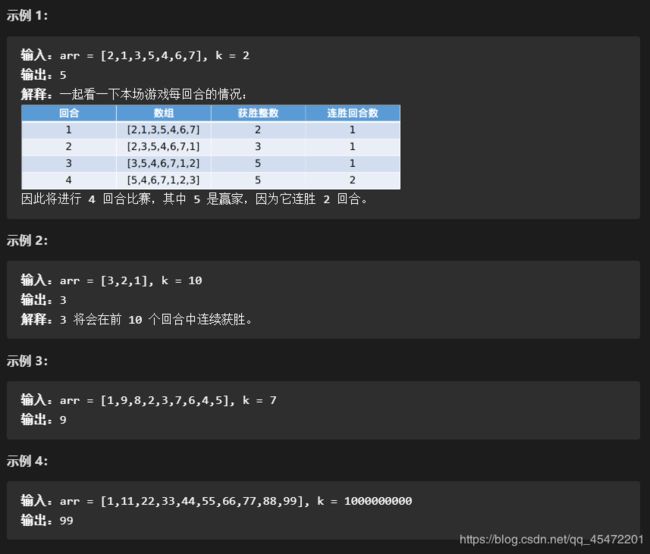
1535. 找出数组游戏的赢家

.给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。

每回合游戏都在数组的前两个元素（即 arr[0] 和 arr[1] ）之间进行。比较 arr[0] 与 arr[1] 的大小，较大的整数将会取得这一回合的胜利并保留在位置 0 ，较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时，游戏结束，该整数就是比赛的 赢家 。

返回赢得比赛的整数。

题目数据 保证 游戏存在赢家。

分析 水题，模拟即可。

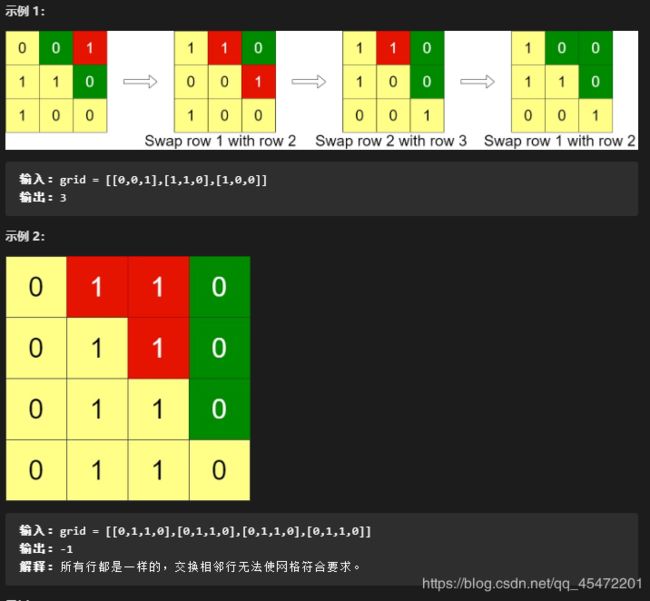
1536. 排布二进制网格的最少交换次数

给你一个 n x n 的二进制网格 grid，每一次操作中，你可以选择网格的 相邻两行 进行交换。

一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。

请你返回使网格满足要求的最少操作次数，如果无法使网格符合要求，请你返回 -1 。

主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。


分析 很容易猜到，我们要将这个二维数组转化为一维数组的形式，此一维数组即为从每一行右边开始向左边遍历，1第一次出现的位置。然后模拟交换步骤即可。

class Solution {
    public int minSwaps(int[][] grid) {
        int ans=0,len=grid.length;
        int[] arr=new int[len];
        for(int i=0;i<len;i++){
            for(int j=len-1;j>=0;j--){
                if(grid[i][j]==1){
                    arr[i]=j;
                    break;
                }
            }
        }
        for(int i=0;i<len;i++){
            if(arr[i]<=i) continue;
            int pos=-1;
            for(int j=i+1;j<len;j++){
                if(arr[j]<=i)
                {
                    pos=j;
                    break;
                }
            }
            if(pos==-1) return -1;
            for(int k = pos; k > i; k--){
                int tmp = arr[k-1];
                arr[k-1] = arr[k];
                arr[k] = tmp;
            }
            ans += (pos - i);
        }
        return ans;
    }
}

1537. 最大得分

你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。

一条 合法路径 定义如下：

选择数组 nums1 或者 nums2 开始遍历（从下标 0 处开始）。
从左到右遍历当前数组。
如果你遇到了 nums1 和 nums2 中都存在的值，那么你可以切换路径到另一个数组对应数字处继续遍历（但在合法路径中重复数字只会被统计一次）。
得分定义为合法路径中不同数字的和。

请你返回所有可能合法路径中的最大得分。

由于答案可能很大，请你将它对 10^9 + 7 取余后返回。

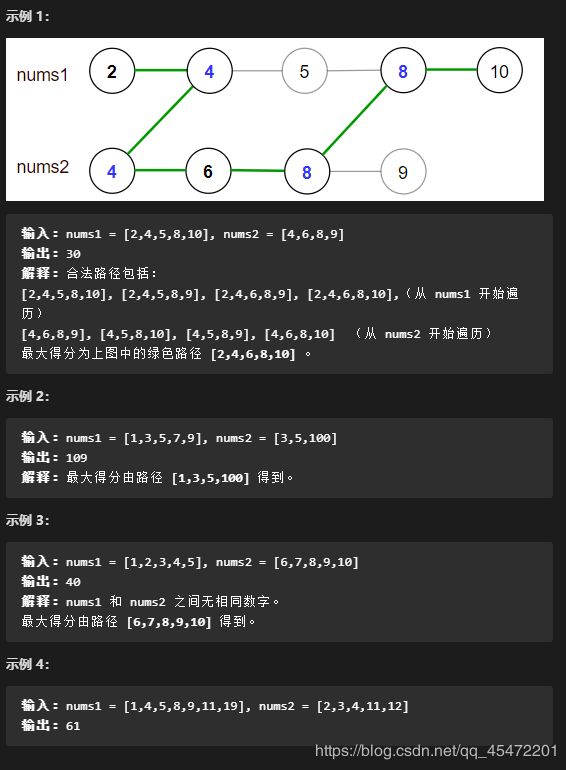
分析 可dp，可双指针。此处使用双指针解答。
以第一个示例画图举例（较为潦草，见谅）

这就是主要算法运作过程。
代码

class Solution {
    public int maxSum(int[] nums1, int[] nums2) {
        long ans1=0,ans2=0;
        int i=0,j=0;
        int mod=(int)(Math.pow(10,9)+7);
        while(i<nums1.length&&j<nums2.length){
            if(nums1[i]<nums2[j]){
                ans1+=nums1[i++];
            }else if(nums1[i]>nums2[j]){
                ans2+=nums2[j++];
            }else{
                ans1=Math.max(ans1,ans2)+nums2[j];
                ans2=ans1;
                i++;
                j++;
            }
        }
        while(i<nums1.length)
        ans1+=nums1[i++];
        while(j<nums2.length)
        ans2+=nums2[j++];
        return (int)(Math.max(ans1,ans2)%mod);
    }
}

但是我们需要验证，这样如何保证是跟题目一样的过程。
ans1 与 ans2 可以看做每次两个数组拥有相同的值的时候，所走的不同的路径，然后在下一次两个数组再次拥有相同的值的时候，将 ans1 与 ans2 整合，继续走不同的路径。思路类似于dp。
而在一个指针已经到达数组末尾时，将另外一个指针之后的数组数字累加，最后输出这两条路径中的最大值即为答案。
算法：双指针、dp

比赛总结

LeetCode的比赛相较cf而言更为简单，不要想太复杂了，而且出题较为有规律，一般竞赛如果有题目考数学与思维较多，那么竞赛大体解法较为偏数学。
而感觉此次模拟较多，我的模拟较为薄弱，还需要加强。