LeetCode 992 K 个不同整数的子数组
给定一个正整数数组 A,如果 A 的某个子数组中不同整数的个数恰好为 K,则称 A 的这个连续、不一定独立的子数组为好子数组。
(例如,[1,2,3,1,2] 中有 3 个不同的整数:1,2,以及 3。)
返回 A 中好子数组的数目。
示例 1:
输出:A = [1,2,1,2,3], K = 2
输入:7
解释:恰好由 2 个不同整数组成的子数组:[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].
示例 2:
输入:A = [1,2,1,3,4], K = 3
输出:3
解释:恰好由 3 个不同整数组成的子数组:[1,2,1,3], [2,1,3], [1,3,4].
提示:
1 <= A.length <= 200001 <= A[i] <= A.length1 <= K <= A.length
解答:
滑动窗口+Map记录窗口元素个数,当窗口长度大于K(说明窗口内部含有重复元素)时,需要考虑窗口内的连续子串可能含有满足元素个数等于K的连续子串。
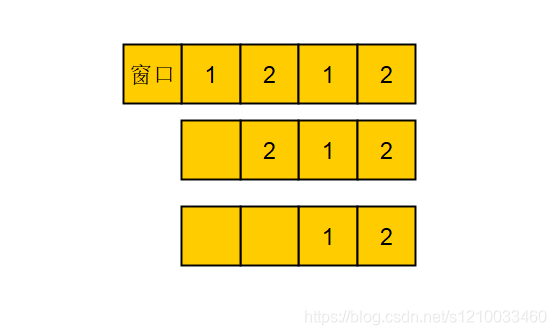
为了避免重复计算子串,采用固定尾部的方法计算,例如"1,2,1,2"的窗口含有两个子串“2,1,2”和“1,2”。
这个方法是我自己写的,有点费时(6500ms),不过通过了,哈哈哈。
class Solution {
int num = 0;
private void sub(int[] A, int K){
Map<Integer, Integer> map = new HashMap<>();
for (int a: A){
map.put(a, map.getOrDefault(a, 0) + 1);
}
int index = 0;
while (map.size() == K){
num++;
if (map.get(A[index]) == 1) { // reduce the first element
map.remove(A[index]);
} else {
map.replace(A[index], map.get(A[index]) - 1);
}
index++;
}
}
public int subarraysWithKDistinct(int[] A, int K) {
int start = 0;
int end = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(A[0], 1);
while (end < A.length) {
if (map.size() == K) {
num++;
if (end - start >= K) {
sub(Arrays.copyOfRange(A,start+1,end+1), K);
}
if (++end < A.length ) { // add the last element
map.put(A[end], map.getOrDefault(A[end], 0) + 1);
}
} else if (map.size() < K) {
if (++end < A.length ) { // add the last element
map.put(A[end], map.getOrDefault(A[end], 0) + 1);
}
} else if (map.size() > K) {
if (map.get(A[start]) == 1) { // reduce the first element
map.remove(A[start]);
} else {
map.replace(A[start], map.get(A[start]) - 1);
}
start++;
}
}
return num;
}
}
双滑动窗口法(官方给的),跟上面的方法类似。使用另外一个窗口处理窗口中满足条件的连续子串,第一个窗口跟上面方法的窗口完全一样,第二个窗口表示“以第一个窗口的end为结尾的窗口B,而且这个窗口B是第一个不满足K条件的窗口(就是while (map.size() == K)这个退出条件表示的sub函数中的map)”,然后两个窗口的差值就是以当前end为结尾的满足K条件的连续子串数。
class Solution {
class Window {
Map<Integer, Integer> count;
int nonzero;
Window() {
count = new HashMap();
nonzero = 0;
}
void add(int x) {
count.put(x, count.getOrDefault(x, 0) + 1);
if (count.get(x) == 1)
nonzero++;
}
void remove(int x) {
count.put(x, count.get(x) - 1);
if (count.get(x) == 0)
nonzero--;
}
int different() {
return nonzero;
}
}
public int subarraysWithKDistinct(int[] A, int K) {
Window window1 = new Window();
Window window2 = new Window();
int ans = 0, left1 = 0, left2 = 0;
for (int right = 0; right < A.length; ++right) {
int x = A[right];
window1.add(x);
window2.add(x);
while (window1.different() > K)
window1.remove(A[left1++]);
while (window2.different() >= K)
window2.remove(A[left2++]);
ans += left2 - left1;
System.out.println(ans);
}
return ans;
}
}