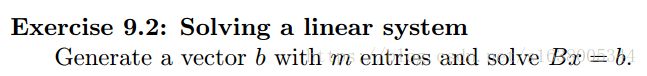Python学习第十一周作业——矩阵运算

Python可以对矩阵进行运算，但需要扩展包numpy和scipy支持。

题目需要生成符合要求的矩阵，使用mat函数实现

import numpy as np
from scipy.linalg import toeplitz
A = np.mat(np.random.normal(size=(200, 500)))
B = np.mat(toeplitz(np.random.normal(size=500), np.random.normal(size=500)))

第一题

进行几种简单的运算，加法，转置，乘法，编写函数计算A(B - λI) 

result1 = A + A
result2 = A.dot(A.T)
result3 = A.T.dot(A)
result4 = A.dot(B)

def practice(factor):
    return A.dot(B-factor*np.eye(500))

第二题

生成向量b，求解线性方程组，解为B的逆矩阵乘b

b = np.random.randint(0,10,500)
x = B.I.dot(b)

第三题

计算范数与奇异值，调用函数norm并穿对应参数实现

F_norm = np.linalg.norm(A, ord='fro')
inf_norm = np.linalg.norm(B, ord=np.inf) 
max_singular = np.linalg.norm(B, ord=2) 
min_singular = np.linalg.norm(B, ord=-2) 

第四题

使用幂迭代法求特征向量

def power_iteration(A, threshold):
    v_k0 = np.random.rand(A.shape[1])
    v_k = np.random.rand(A.shape[1])
    count = 0
    while np.linalg.norm(v_k - v_k0) >= threshold:
        v_k0 = v_k
        u_k = np.dot(A, v_k0)
        m_k = np.max(u_k)
        v_k = u_k/m_k
        count += 1

    return (np.max(u_k), v_k, count)

Z = np.random.normal(size=(200,200))
power_iteration(Z, 0.0001)

第五题

寻找n,p和最大奇异值的关系，看图可以发现最大奇异值与n正相关，与p负相关

from scipy import linalg
from matplotlib import pyplot as plt  

def get_singular_value(size, p):
    t = np.random.rand(size, size) > p
    C = np.zeros((size,size))
    C[t]=1
    singular = linalg.svd(C)[1]
    max_singular = np.max(singular)
    return max_singular

singulars = []
for n in range(5, 100):
    singulars.append(get_singular_value(n, 0.6))
plt.plot(range(5, 100), singulars)

singulars = []
for n in np.rand(30):
    singulars.append(get_singular_value(100, n))
plt.plot(np.rand(30),singulars)

plt.show()

第六题

寻找A中最接近z的元素

def find_nearest(A, z):
    return A[np.argmin(np.abs(A-z))]