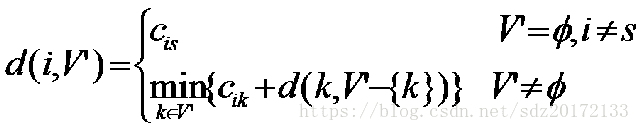状态压缩DP的TSP问题
1.问题定义
TSP问题(旅行商问题)是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
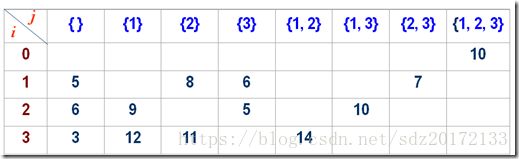
假设现在有四个城市,0,1,2,3,他们之间的代价如图一,可以存成二维表的形式
现在要从城市0出发,最后又回到0,期间1,2,3都必须并且只能经过一次,使代价最小。
2.动态规划可行性
设s, s1, s2, …, sp, s是从s出发的一条路径长度最短的简单回路,假设从s到下一个城市s1已经求出,则问题转化为求从s1到s的最短路径,显然s1, s2, …, sp, s一定构成一条从s1到s的最短路径,所以TSP问题是构成最优子结构性质的,用动态规划来求解也是合理的。
3.推导动态规划方程
假设从顶点s出发,令d(i, V’)表示从顶点i出发经过V’(是一个点的集合)中各个顶点一次且仅一次,最后回到出发点s的最短路径长度。
推导:(分情况来讨论)
①当V’为空集,那么d(i, V’),表示从i不经过任何点就回到s了,如上图的 城市3->城市0(0为起点城市)。此时d(i, V’)=Cis(就是 城市i 到 城市s 的距离)、
②如果V’不为空,那么就是对子问题的最优求解。你必须在V’这个城市集合中,尝试每一个,并求出最优解。
d(i, V’)=min{Cik + d(k, V’-{k})}
注:Cik表示你选择的城市和城市i的距离,d(k, V’-{k})是一个子问题。
综上所述,TSP问题的动态规划方程就出来了:
4.实例分析
现在对问题定义中的例子来说明TSP的求解过程。(假设出发城市是 0城市)
①我们要求的最终结果是d(0,{1,2,3}),它表示,从城市0开始,经过{1,2,3}之中的城市并且只有一次,求出最短路径.
②d(0,{1,2,3})是不能一下子求出来的,那么他的值是怎么得出的呢?看上图的第二层,第二层表明了d(0,{1,2,3})所需依赖的值。那么得出:
d(0,{1,2,3})=min {
C01+d(1,{2,3})
C02+d{2,{1,3}}
C03+d{3,{1,2}}
}
③d(1,{2,3}),d(2,{1,3}),d(3,{1,2})同样也不是一步就能求出来的,它们的解一样需要有依赖,就比如说d(1,{2,3})
d(1,{2,3})=min{
C12+d(2,{3})
C13+d(3,{2})
}
d(2,{1,3}),d(3,{1,2})同样需要这么求。
④按照上面的思路,只有最后一层的,当当V’为空集时,Cis的值才可以求,它的值是直接从
这张表里求得的。
5.编程思路
将d(i, V’)转换成二维表,d[i][j]
在程序中模拟填表的过程,主要要考虑到j这个参数的表示,它要代表一个集合,可以用二维数组来表示。
6.代码实现
记忆化搜索DP:
#include
#include
#include
#include
using namespace std;
#define M 19
#define INF 0x3f3f3f3f
int n;
int mp[M][M]; //注意mp是从0行开始的
int dp[1<<11][M];
/*将S看作一个长度为n的bit流,
第几号节点访问过就把S的第几号节点置为1,其他都是0,
这样就可以将状态压缩成了一个数字来表示,并且有一一对应性。*/
int slove(int s,int v) //记忆化搜索
{
if(dp[s][v] >= 0) return dp[s][v]; //已经有结果
if(s == (1<> u) & 1)) //判断是否访问过,如果u这一位是0,即没有访问过
ret = min(ret,slove(s|(1< 递推DP:
#include
#include
using namespace std;
int n,INF=1e9;
int dp[1<<10001][10001],d[10001][10001];
//注意d是从0开始的
int main()
{
cin>>n;
for(int i=0;i>d[i][j];
for(int S=0;S<(1<=0;S--){
for(int v=0;v>u&1)){//取出整数S在二进制表示下的第u位
dp[S][v]=min(dp[S][v],dp[S|1< 7.经典例题
POJ 3311 Hie with the Pie 状态压缩DP TSP问题(两种方法)
HDU 5418 Victor and World 状压DP的TSP问题
hdu3001 Traveling (三进制状态压缩dp)