集成学习 (投票分类器 & bagging/pasting & RandomForest & Boosting)
集成学习
本文主要介绍
- voting (投票学习器)
- bagging / pasting
3.随机森林- boosting
1.集成学习概述
1.1 概述
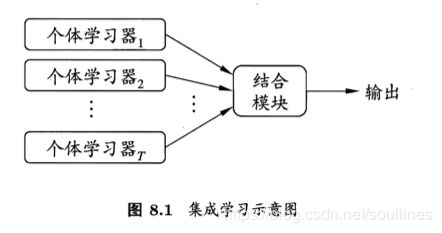
集成学习通过结合多个单一学习器,并聚合其预测结果的学习任务,也可以称作多分类系统等,下面是集成学习的概要图:
- 单一的学习器可以被称为个体学习器,聚合的过程对应结合模块
- 根据学习器是否一致可以分为 同质 和 异质
- 同质集成中的个体学习器被称为"基学习器"
为了理解集成学习,我们先举一个例子来理解集成学习:
我们对一个问题疑惑,那么向基数比较大的群众进行问卷调查,那么根据每个人的回答以少数服从多数的原则来确定问题的答案,根据大数定理往往会获得一个比较满意的答案.
同理运用到机器学习中,一堆弱学习模型有时候单个的预测准确率仅仅比随机概率要大一些,那么我们可以根据所有预测器的预测结果占比来输出最终的预测结果.
大部分时候基于多预测器的集成学习要优于单个预测,这便是集成学习,下面是继承学习的公式:
H ( x ) = s i g n ( ∑ i = 1 T h i ( x ) ) H(x) = sign(\sum_{i=1}^T h_i(x)) H(x)=sign(i=1∑Thi(x))
1.2 基学习器的选择
集成学习一般通过多个学习器进行结合,然后获得比单一学习器显著优越的泛化性能,这对"弱学习器"的优化尤为重要;
但是实践中并不总是集成学习器优于单个学习器,我们需要注重个体学习器的质量,下面来看一个例子:

上面三个例子在集成过程中,可以看到集成学习并不能所有情况下都符合预期
- 图a,每个个体学习器准确率是 66.7 % 66.7\% 66.7%,但是集成之后准确率可以达到 100 % 100\% 100%,那么 集成提升性能
- 图b,每个个体学习率准确率是 66.7 % 66.7\% 66.7%,那么 集成之后准确率依旧
- 图c,集合前的准确率是 66.7 % 66.7\% 66.7%,但是集成之后变成 0 % 0\% 0%,那么 集成起到了负作用
那么可以看到 有效的个体学习器可以提升集成学习器的性能, 那么我们此时需要思考一个问题,如何选择 优秀的个体学习器 :
- 个体学习器要有一定的 准确性
- 个体学习器要有 多样性, 学习器之间要有差异性,这样有利于范化
到此为止,可以知道个体学习器的选取,便是集成学习的难点和核心
集成学习根据并行/串行,或者说是否更新后序学习器的样本数据权重可以分成两大类:
- voting(投票分类器) / bagging & pasting / 随机森林,并行运行所有个体学习器,然后聚合预测结果
- bosting, 重训运行每个个体学习器,然后每次训练完一个便更新预测错误的样本权重,使得下一个个体学习器,可以更加关注这些样本
2.投票分类器
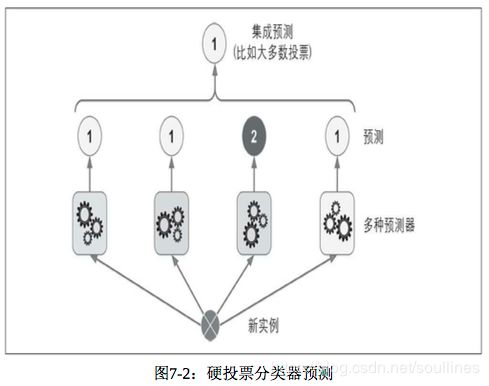
- 1.训练多种分类器的集成学习模型:logits分类器,SVM分类器,随机森林分类器…
- 2.根据不同种类的分类器输出结果进行统计,将占比最大的结果作为本次投票的最终结果输出
这就是投票分类器,这样的集成模型基于大数定理要高于预测模型序列中任何一个最优模型的准确率,也就是说:
在数据足够大的基础上,这样可以将一系列弱学习器,通过集合的方式,将预测模型变成一个强学习器
下面用scikit-learn来实现投票分类器:
# 使用scikit中自带的卫星数据
moons = make_moons(n_samples=20000)
# 逻辑回归分类器
log_clf = LogisticRegression()
# 随机森林分类器
rnd_clf = RandomForestClassifier()
# 支持向量机分类器
svm_clf = SVC(probability=True)
# 集成以上3种分类器的投票分类器
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='soft'
)
# 分别输出 逻辑回归,随机森林,svm,投票分类器的准确率
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(x_train, y_train)
y_pred = clf.predict(x_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
out:
LogisticRegression 0.891
RandomForestClassifier 1.0
SVC 1.0
VotingClassifier 1.0
-
注意 voting_clf 中voting参数:
-
hard: 独立个体的大多数类别就是改预测器的预测结果
模型1: A-0.9 B-0.1 模型2: A-0.8 B-0.9 # A 1票(模型1) B 3票 Hard voting预测结果B 模型3: A-0.3 B-0.2 模型4: A-0.4 B-0.3 -
soft: 将每个预测器对某一类别的概率进行平均,最后横向比较
模型1: A-0.9 B-0.1 模型2: A-0.8 B-0.9 # A 平均概率:0.6 B 平均概率:0.375 Soft voting预测结果A 模型3: A-0.3 B-0.2 模型4: A-0.4 B-0.3
-
3. bagging 和 pasting
3.1概述
上面提到的投票分类是:通过集成不同分类器进行集成分类
bagging和pasting则有些不同:集成序列中每一个预测器都是相同的,但是每个预测器在不同的训练自己上进行训练,那么既然是不同的训练子集,那么就应该在样本集上进行子样本的抽取,这也是 bagging 和 pasting 的区别:
- bagging是有放回的抽取
- pasting是没有放回的抽取
也就是说bagging 和 pasting 都允许在样本集上多次抽样,但是 pasting 因为是不放回的抽取,所以 pasting 的子集不会交叉

- 1.对所有预测进行统计
- 2.聚合所有预测器的预测结果,分类场景可以使用少数服从多数的原则计算最终结果或者计算所有列别预测概率平均值然后在类别的方向进行横向比较,回归场景直接计算平均值即可
集成模式相比于单一模型场景可以有效的降低偏差以及方差
3.2 算法推导,以bagging为例
- II表示示性函数,表示当括号内条件成立时取值为1,否则为0.
由于bagging是有放回的抽取,所以会用到约 63.2 % 63.2\% 63.2%的数据,所以剩下的 36.8 % 36.8\% 36.8%可以进行包外估计:
-
H o o b ( x ) H^{oob}(x) Hoob(x)表示预测的概率, T是个体学习器的数目, D o o b D_{oob} Doob代表包外的样本数目
-
ϵ \epsilon ϵ 标识误差率
H o o b = s i g n ( ∑ t = 1 T h t ( x ) ) H^{oob} = sign (\sum_{t=1}^Th_t(x)) Hoob=sign(t=1∑Tht(x))
ϵ = 1 D o o d ∑ x , y ϵ D o o d ( H o o d ( x ) ≠ y ) / T \epsilon = \frac{1}{D_{ood}} \sum_{x,y \epsilon D_{ood}} (H^{ood}(x) \neq y)/T ϵ=Dood1x,yϵDood∑(Hood(x)=y)/T
3.3 代码实现
代码实现,基于多个决策树的bagging和pasting 实现:
# bagging 实现
bag_clf = BaggingClassifier(
DecisionTreeClassifier(), n_estimators=500, max_samples=100,
bootstrap=True, n_jobs=-1, random_state=42
)
# pasting 实现
past_clf = BaggingClassifier(
DecisionTreeClassifier(), n_estimators=500, max_samples=100,
bootstrap=False, n_jobs=-1, random_state=42
)
下面是单个 决策树 和上面 bagging or pasting 的对比图:
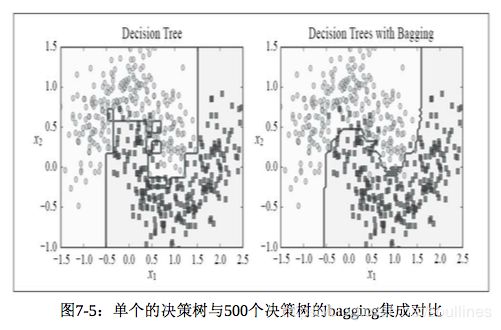
- 可以明显看到,集成模型的边界拟合度更高,方差更小,同样偏差也会更低
4 随机森林
随机森林其实就是Bagging的一个扩展变体,下面直接看代码即可:
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1)
rnd_clf.fit(x_train, y_train)
y_pred = rnd_clf.predict(x_test)
print(accuracy_score(y_test, y_pred))
print(rnd_clf.feature_importances_)
'''
下面的bagging分类器 等同于上面的随机森林
'''
bag_clf = BaggingClassifier(
DecisionTreeClassifier(splitter='random', max_leaf_nodes=16),
n_estimators=500, max_samples=1.0, bootstrap=True, n_jobs=-1
)
bag_clf.fit(x_train, y_train)
y_pred = bag_clf.predict(x_test)
print(accuracy_score(y_test, y_pred))
有一点不同,随机森林通常具有更强的泛化能力和训练效率:
- bagging使用"确定型"决策树,在选择划分属性时要对结点的所有属性进行考察
- 随机森林使用"随机性"决策树则只需要考察一个属性子集即可
5 Boosting
Boosting算法的原理:
先从初始训练集中训练出一个基学习器,再根据当前基学习器的训练误差进行分析,将错分的样本提升权值,使得下一个学习器更加关注这些权值,重复这个过程知道遍历至最后一个学习器,然后将 T T T个基学习器的预测结果进行加权结合
5.1 接着看boosting的算法流程
全局数据: 个体学习器数T,训练数据 D t D_t Dt t = (1,2….T) ,标签是y
-
训练数据的取样概率初始相等的,均为 1 m \frac{1}{m} m1, 串行训练基学习器:
h t = ξ ( D , D t ) h_t = \xi(D,D_t) ht=ξ(D,Dt)
-
计算预测误差,并计算权重:
ϵ t = P x D t , y D t ( h t ( x ) ≠ y ) \epsilon_t = P_{x~D_t,y~D_t}(h_t(x) \neq y) ϵt=Px Dt,y Dt(ht(x)=y)
α t = 1 2 I n ( 1 − ϵ t ϵ t ) \alpha_t = \frac{1}{2}In(\frac{1-\epsilon_t}{\epsilon_t}) αt=21In(ϵt1−ϵt)
-
更新当前样本集每个样本的取样权重:
D t + 1 ( x ) = D t ( x ) Z t ∗ e x p ( − α t ) i f h ( x ) = y D_t+1(x) = \frac{D_t(x)}{Z_t} * exp(-\alpha_t) if h(x) = y Dt+1(x)=ZtDt(x)∗exp(−αt)ifh(x)=y
D t + 1 ( x ) = D t ( x ) Z t ∗ e x p ( α t ) i f h ( x ) ≠ y D_t+1(x) = \frac{D_t(x)}{Z_t} * exp(\alpha_t) if h(x) \neq y Dt+1(x)=ZtDt(x)∗exp(αt)ifh(x)=y
-
更新权重之后循环上述过程,知道最后一个学习器,然后聚合所有学习器的结果:
H ( x ) = s i g n ( ∑ t = 1 T α t h t ( x ) ) H(x) = sign(\sum_{t=1}^T\alpha_th_t(x)) H(x)=sign(t=1∑Tαtht(x))
但是权重 α \alpha α为什么这样定义呢,我们继续往下看
-
AdaBoost的损失函数
l ( H ∣ D ) = E x D [ e − y H ( x ) ] l(H|D) = E_{x~D}[e^{-yH(x)}] l(H∣D)=Ex D[e−yH(x)]
-
对 H ( x ) H(x) H(x)求偏导
d l ( H ∣ D ) d ( H ( x ) ) = − y e − y H ( x ) \frac{dl(H|D)}{d(H(x))} = -y\;e^{-yH(x)} d(H(x))dl(H∣D)=−ye−yH(x)
又因为 y ϵ { 1 , − 1 } y\epsilon \lbrace{1,-1}\rbrace yϵ{1,−1}
d l ( H ∣ D ) d ( H ( x ) ) = − y e − y H ( x ) = − e − H ( x ) P ( y = 1 ∣ x ) + e H ( x ) P ( y = − 1 ∣ x ) \frac{dl(H|D)}{d(H(x))} = -y\;e^{-yH(x)} = -e^{-H(x)}P(y=1|x) + e^{H(x)}P(y=-1|x) d(H(x))dl(H∣D)=−ye−yH(x)=−e−H(x)P(y=1∣x)+eH(x)P(y=−1∣x)
-
假设误差率是 ϵ \epsilon ϵ,那么:
P ( y = − 1 ∣ x ) = ϵ P ( y = 1 ∣ x ) = ( 1 − ϵ ) P(y=-1|x) = \epsilon \;\;\;\; P(y=1|x) =(1- \epsilon) P(y=−1∣x)=ϵP(y=1∣x)=(1−ϵ)
d l ( H ∣ D ) d ( H ( x ) ) = − y e − y H ( x ) = − e − H ( x ) ( 1 − ϵ ) + e H ( x ) ϵ \frac{dl(H|D)}{d(H(x))} = -y\;e^{-yH(x)} = -e^{-H(x)}(1-\epsilon) + e^{H(x)}\epsilon d(H(x))dl(H∣D)=−ye−yH(x)=−e−H(x)(1−ϵ)+eH(x)ϵ
-
又因为在AdaBoots中,且个体学习器是串行执行:
H ( x ) = s i g n ( ∑ t = 1 T α t h t ( x ) ) H(x) = sign(\sum_{t=1}^T\alpha_th_t(x)) H(x)=sign(t=1∑Tαtht(x))
d l ( H ∣ D ) d ( H ( x ) ) = − e − H ( x ) ( 1 − ϵ ) + e H ( x ) ϵ = − e − α t h t ( x ) ( 1 − ϵ ) + e α t h t ( x ) ϵ \frac{dl(H|D)}{d(H(x))} = -e^{-H(x)}(1-\epsilon) + e^{H(x)}\epsilon = -e^{-\alpha_th_t(x)}(1-\epsilon) + e^{\alpha_th_t(x)}\epsilon d(H(x))dl(H∣D)=−e−H(x)(1−ϵ)+eH(x)ϵ=−e−αtht(x)(1−ϵ)+eαtht(x)ϵ
- 又因为 h t ( x ) ϵ { − 1 , 1 } h_t(x) \epsilon \lbrace{-1,1}\rbrace ht(x)ϵ{−1,1}
d l ( H ∣ D ) d ( H ( x ) ) = e − α t h t ( x ) ( 1 − ϵ ) + e α t h t ( x ) ϵ = e − α t ( 1 − ϵ t ) + e α t ϵ t \frac{dl(H|D)}{d(H(x))} = e^{-\alpha_th_t(x)}(1-\epsilon) + e^{\alpha_th_t(x)}\epsilon = e^{-\alpha_t}(1-\epsilon_t) + e^{\alpha_t}\epsilon_t d(H(x))dl(H∣D)=e−αtht(x)(1−ϵ)+eαtht(x)ϵ=e−αt(1−ϵt)+eαtϵt
-
上式对 α t \alpha_t αt求导,则:
d ( e − α t ( 1 − ϵ ) + e α t ϵ ) d α t = − e − α t ( 1 − ϵ t ) + e α t ϵ t \frac{d( e^{-\alpha_t}(1-\epsilon) + e^{\alpha_t}\epsilon)}{d\alpha_t} = -e^{-\alpha_t}(1-\epsilon_t) + e^{\alpha_t}\epsilon_t dαtd(e−αt(1−ϵ)+eαtϵ)=−e−αt(1−ϵt)+eαtϵt
-
令上述式子等于0,则:
α t = 1 2 I n ( 1 − ϵ t ϵ t ) \alpha_t = \frac{1}{2}In(\frac{1-\epsilon_t}{\epsilon_t}) αt=21In(ϵt1−ϵt)
5.2 代码实现
'''
提升法AdaBoost:
仅仅是计算每一个分类器的权重而已
'''
'''
最后 会获得每一个分类器的权重,然后利用投票法进行预测
'''
'''
下面来看scikit-learn代码
基于200个单层的决策树
'''
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1), n_estimators=200,
algorithm='SAMME.R', learning_rate=0.5
)
ada_clf.fit(x_train, y_train)
y_pred = ada_clf.predict(x_test)
print(accuracy_score(y_test, y_pred))
欢迎补充,感谢阅读 ^ ^