CCF 全国信息学奥林匹克联赛(NOIP2018)复赛真题
CCF 全国信息学奥林匹克联赛(NOIP2018)复赛
普及组 (请选手务必仔细阅读本页内容)
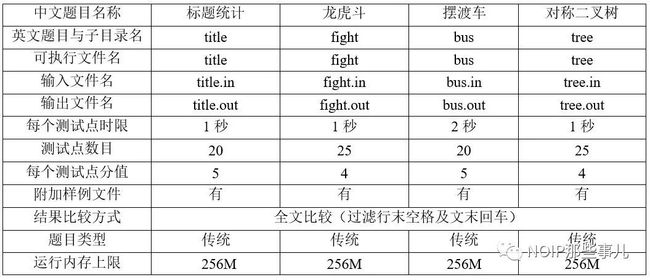
一.题目概况
二.提交源程序文件名
三.编译命令(不包含任何优化开关)
注意事项:
1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是 0。
3、全国统一评测时采用的机器配置为:
Intel(R) Core(TM) i7-8700K CPU @ 3.70GHz,内存32GB。上述时限以此配置为准。
4、只提供 Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的 NOI Linux 下进行,各语言的编译器版本以其为准。
1. 标题统计
(title.cpp/c/pas)
【问题描述】
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符?
注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。
统计标题字符数时,空格和换行符不计算在内。
【输入格式】
输入文件名为 title.in。
输入文件只有一行,一个字符串 s。
【输出格式】
输出文件名为 title.out。
输出文件只有一行,包含一个整数,即作文标题的字符数(不含空格和换行符)。
【输入输出样例 1】
| title.in |
title.out |
| 234 |
3 |
见选手目录下的 title/title1.in 和 title/title1.ans。
【输入输出样例 1 说明】
标题中共有 3 个字符,这 3 个字符都是数字字符。
【输入输出样例 2】
| title.in |
title.out |
| Ca 45 |
4 |
见选手目录下的 title/title2.in 和 title/title2.ans。
【输入输出样例 2 说明】
标题中共有 5 个字符,包括 1 个大写英文字母,1 个小写英文字母和 2 个数字字符,还有 1 个空格。由于空格不计入结果中,故标题的有效字符数为 4 个。
【数据规模与约定】
规定 |s| 表示字符串 s 的长度(即字符串中的字符和空格数)。
对于 40% 的数据,1 ≤ |s| ≤ 5,保证输入为数字字符及行末换行符。
对于 80% 的数据,1 ≤ |s| ≤ 5,输入只可能包含大、小写英文字母、数字字符及行末换行符。
对于 100% 的数据,1 ≤ |s| ≤ 5,输入可能包含大、小写英文字母、数字字符、空格和行末换行符。
2. 龙虎斗
(fight.cpp/c/pas)
【问题描述】
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏,游戏的棋盘是一条线段,线段上有 n个兵营(自左至右编号 1 ~ n),相邻编号的兵营之间相隔 1 厘米,即棋盘为长度为n − 1 厘米的线段。i 号兵营里有 ci 位工兵。
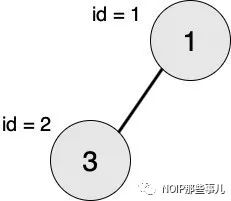
下面图 1 为 n = 6 的示例:
图 1. n = 6的示例
轩轩在左侧,代表“龙”;凯凯在右侧,代表“虎”。他们以 m 号兵营作为分界,靠左的工兵属于龙势力,靠右的工兵属于虎势力,而第 m 号兵营中的工兵很纠结,他们不属于任何一方。
一个兵营的气势为:该兵营中的工兵数 × 该兵营到 m 号兵营的距离;参与游戏一方的势力定义为:属于这一方所有兵营的气势之和。
下面图 2 为 n = 6, m = 4 的示例,其中红色为龙方,黄色为虎方:
图 2. n = 6, m = 4的示例
游戏过程中,某一刻天降神兵,共有 s1 位工兵突然出现在了 p1 号兵营。作为轩轩和凯凯的朋友,你知道如果龙虎双方气势差距太悬殊,轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续,你需要选择一个兵营 p2,并将你手里的 s2 位工兵全部派往兵营 p2,使得双方气势差距尽可能小。
注意:你手中的工兵落在哪个兵营,就和该兵营中其他工兵有相同的势力归属(如果落在 m 号兵营,则不属于任何势力)。
【输入格式】
输入文件名为 fight.in。
输入文件的第一行包含一个正整数 n,代表兵营的数量。
接下来的一行包含 n 个正整数,相邻两数之间以一个空格分隔,第 i个正整数代表编号为 i 的兵营中起始时的工兵数量 ci。
接下来的一行包含四个正整数,相邻两数间以一个空格分隔,分别代表 m, p1, s1, s2。
【输出格式】
输出文件名为 fight.out。
输出文件有一行,包含一个正整数,即 p2,表示你选择的兵营编号。如果存在多个编号同时满足最优,取最小的编号。
【输入输出样例 1】
| fight.in |
fight.out |
| 6 2 3 2 3 2 3 4 6 5 2 |
2
|
见选手目录下的 fight/fight1.in 和 fight/fight1.ans。
【输入输出样例 1 说明】见问题描述中的图 2。
双方以 m = 4 号兵营分界,有 s1 = 5 位工兵突然出现在 p1 = 6 号兵营。
龙方的气势为:
2 × (4 − 1) + 3 × (4 − 2) + 2 × (4 − 3) = 14
虎方的气势为:
2 × (5 − 4) + (3 + 5) × (6 − 4) = 18
当你将手中的 s2 = 2 位工兵派往 p2 = 2 号兵营时,龙方的气势变为:
14 + 2 × (4 − 2) = 18
此时双方气势相等。
【输入输出样例 2】
| fight.in |
fight.out |
| 6 1 1 1 1 1 16 5 4 1 1 |
1
|
见选手目录下的 fight/fight2.in 和 fight/fight2.ans。
【输入输出样例 2 说明】
双方以 m = 5 号兵营分界,有 s1 = 1 位工兵突然出现在 p1 = 4 号兵营。
龙方的气势为:
1 × (5 − 1) + 1 × (5 − 2) + 1 × (5 − 3) + (1 + 1) × (5 − 4) = 11
虎方的气势为:
16 × (6 − 5) = 16
当你将手中的 s2 = 1 位工兵派往 p2 = 1 号兵营时,龙方的气势变为:
11 + 1 × (5 − 1) = 15
此时可以使双方气势的差距最小。
【输入输出样例 3】
见选手目录下的 fight/fight3.in 和 fight/fight3.ans。
【数据规模与约定】
1 < m < n, 1 ≤ p1 ≤ n。
对于 20% 的数据,n = 3, m = 2, ci = 1, s1, s2 ≤ 100。
另有 20% 的数据,n ≤ 10, p1 = m, ci = 1, s1, s2 ≤ 100。
对于 60% 的数据,n ≤ 100, ci = 1, s1, s2 ≤ 100。
对于 80% 的数据,n ≤ 100, ci, s1, s2 ≤ 100。
对于 100% 的数据,n ≤ 105, ci, s1, s2 ≤ 109。
3. 摆渡车
(bus.cpp/c/pas)
【问题描述】
有 n 名同学要乘坐摆渡车从人大附中前往人民大学,第 i 位同学在第 ti 分钟去等车。只有一辆摆渡车在工作,但摆渡车容量可以视为无限大。摆渡车从人大附中出发、把车上的同学送到人民大学、再回到人大附中(去接其他同学),这样往返一趟总共花费 m 分钟(同学上下车时间忽略不计)。摆渡车要将所有同学都送到人民大学。
凯凯很好奇,如果他能任意安排摆渡车出发的时间,那么这些同学的等车时间之和最小为多少呢?
注意:摆渡车回到人大附中后可以即刻出发。
【输入格式】
输入文件名为 bus.in。
第一行包含两个正整数 n,m,以一个空格分开,分别代表等车人数和摆渡车往返一趟的时间。
第二行包含 n 个正整数,相邻两数之间以一个空格分隔,第 i 个非负整数 ti 代表第 i 个同学到达车站的时刻。
【输出格式】
输出文件名为 bus.out。
输出一行,一个整数,表示所有同学等车时间之和的最小值(单位:分钟)。
【输入输出样例 1】
| bus.in |
bus.out |
| 5 1 3 4 4 3 5 |
0
|
见选手目录下的 bus/bus1.in 和 bus/bus1.ans。
【输入输出样例 1 说明】
同学 1 和同学 4 在第 3 分钟开始等车,等待 0 分钟,在第 3 分钟乘坐摆渡车
出发。摆渡车在第 4 分钟回到人大附中。
同学 2 和同学 3 在第 4 分钟开始等车,等待 0 分钟,在第 4 分钟乘坐摆渡车
出发。摆渡车在第 5 分钟回到人大附中。
同学 5 在第 5 分钟开始等车,等待 0 分钟,在第 5 分钟乘坐摆渡车出发。自此所有同学都被送到人民大学。总等待时间为 0。
【输入输出样例 2】
| bus.in |
bus.out |
| 5 5 11 13 1 5 5 |
4
|
见选手目录下的 bus/bus2.in 和 bus/bus2.ans。
【输入输出样例 2 说明】
同学3在第1 分钟开始等车,等待 0 分钟,在第1 分钟乘坐摆渡车出发。
摆渡车在第 6 分钟回到人大附中。
同学4和同学5在第5分钟开始等车,等待1 分钟,在第 6 分钟乘坐摆渡车出发。
摆渡车在第11分钟回到人大附中。
同学1在第11分钟开始等车,等待 2 分钟;
同学2在第13分钟开始等车,等待 0 分钟。
他/她们在第13分钟乘坐摆渡车出发。
自此所有同学都被送到人民大学。总等待时间为 4。可以证明,没有总等待时间小于 4 的方案。
【输入输出样例 3】
见选手目录下的 bus/bus3.in 和 bus/bus3.ans。
【数据规模与约定】
对于10%的数据,n ≤ 10, m = 1, 0 ≤ ti ≤ 100。
对于30% 的数据,n ≤ 20, m ≤ 2, 0 ≤ ti ≤ 100。
对于50%的数据,n ≤ 500, m ≤ 100, 0 ≤ ti ≤ 104。
另有20%的数据,n ≤ 500, m ≤ 10, 0 ≤ ti ≤ 4 × 106 。
对于 100% 的数据,n ≤ 500, m ≤ 100, 0 ≤ ti ≤ 4 × 106。
4. 对称二叉树
(tree.cpp/c/pas)
【问题描述】
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
1. 二叉树;
2. 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
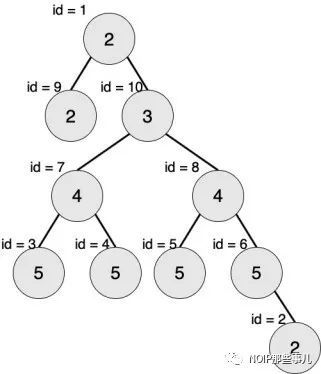
下图中节点内的数字为权值,节点外的 id 表示节点编号。
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。
本题中约定,以节点 T 为子树根的一棵“子树”指的是:节点 T 和它的全部后代节点构成的二叉树。
【输入格式】
输入文件名为 tree.in。
第一行一个正整数 n,表示给定的树的节点的数目,规定节点编号 1~n,其中节点1 是树根。
第二行 n 个正整数,用一个空格分隔,第 i 个正整数 vi 代表节点 i 的权值。
接下来 n 行,每行两个正整数 li, ri ,分别表示节点 i 的左右孩子的编号。
如果不存在左 / 右孩子,则以 −1 表示。两个数之间用一个空格隔开。
【输出格式】
输出文件名为 tree.out。
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
【输入输出样例 1】
| tree.in |
tree.out |
| 2 1 3 2 -1 -1 -1 |
1
|
见选手目录下的 tree/tree1.in 和 tree/tree1.ans。
【输入输出样例 1 说明】
最大的对称二叉子树为以节点 2 为树根的子树,节点数为 1。
【输入输出样例 2】
| tree.in |
tree.out |
| 10 2 2 5 5 5 5 4 4 2 3 9 10 -1 -1 -1 -1 -1 -1 -1 -1 -1 2 3 4 5 6 -1 -1 7 8
|
1
|
见选手目录下的 tree/tree2.in 和 tree/tree2.ans。
【输入输出样例 2 说明】
最大的对称二叉子树为以节点 7 为树根的子树,节点数为 3。
【输入输出样例 3】
见选手目录下的 tree/tree3.in 和 tree/tree3.ans。
【数据规模与约定】
共 25 个测试点。
vi ≤ 1000。
测试点 1~3,n ≤ 10,保证根结点的左子树的所有节点都没有右孩子,根结点的右子树的所有节点都没有左孩子。
测试点 4~8,n ≤ 10。
测试点 9~12,n ≤ 105 ,保证输入是一棵“满二叉树”。
测试点 13~16,n ≤ 105,保证输入是一棵“完全二叉树”。
测试点 17~20,n ≤ 105,保证输入的树的点权均为 1。
测试点 21~25,n ≤ 106。
本题约定:
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。
树中任一节点的层次等于其父亲节点的层次加 1。
树的深度:树中节点的最大层次称为树的深度。
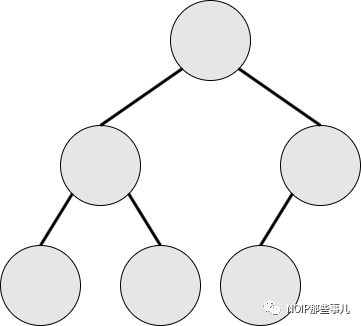
满二叉树:设二叉树的深度为 h,且二叉树有 2h−1 个节点,这就是满二叉树。
满二叉树(深度为 3)
完全二叉树:设二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 ℎ 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树(深度为 3)
完全二叉树(深度为 3)
![]()
![]()
微信搜索
NOIP那些事儿
长按识别左侧二维码,关注我