TreeMap底层原理解析（jdk1.8）
TreeMap底层原理解析
一.TreeMap概述
- TreeMap存储K-V键值对，通过红黑树（R-B tree）实现；
- TreeMap继承了NavigableMap接口，NavigableMap接口继承了SortedMap接口，可支持一系列的导航定位以及导航操作的方法，当然只是提供了接口，需要TreeMap自己去实现；
- TreeMap实现了Cloneable接口，可被克隆，实现了Serializable接口，可序列化；
- TreeMap因为是通过红黑树实现，红黑树结构天然支持排序，默认情况下通过Key值的自然顺序进行排序；
二.TreepMap的成员变量
/**
* 我们前面提到TreeMap是可以自动排序的，默认情况下comparator为null，
* 这个时候按照key的自然顺序进行排序
* 我们可以通过TreepMap的构造函数传递Comparator的实现类，这样TreepMap
* 中的元素节点即key就由我们自定义的Comparator来进行排序
*/
private final Comparator<? super K> comparator;
/**
* 指向TreepMap的根节点
*/
private transient Entry<K,V> root;
/**
* Map中key-val对的数量，也即是红黑树中节点Entry的数量
*/
private transient int size = 0;
/**
* 树的结构修改次数.
*/
private transient int modCount = 0;
三.TreeMap中节点的类型
从上面成员变量发现根节点root是Entry类型，即TreeMap中节点的类型是Entry类型。
Entry类为TreeMap中的静态内部类，如下：
static final class Entry<K,V> implements Map.Entry<K,V> {
K key; //该节点的键
V value; //该节点的值
Entry<K,V> left; //定义了该节点的左孩子
Entry<K,V> right; //定义了该节点的右孩子
Entry<K,V> parent; //定义了该节点的父节点
boolean color = BLACK; //该节点的颜色
/**
*构造器
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* 获取节点的key
*/
public K getKey() {
return key;
}
/**
* 获取节点的value值
*/
public V getValue() {
return value;
}
/**
* 用新值替换当前值，并返回当前值
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
四.TreepMap的构造函数
/**
* 空参构造函数，按照key的自然顺序排列
*/
public TreeMap() {
comparator = null;
}
/**
* 传递Comparator具体实现，按照该实现规则进行排序
*/
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
/**
* 传递一个map实体构建TreeMap,按照默认规则排序
*/
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
/**
* 传递一个map实体构建TreeMap,按照传递的map的排序规则进行排序
*/
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
五.示例
public class TreeMapDemo {
public static void main(String[] args) {
TreeMap<Integer, String> map = new TreeMap<Integer,String>();
map.put(1,"刘宇才");
map.put(2, "邓雪绸");
System.out.println(map); //{1=刘宇才, 2=邓雪绸}
map.put(1,"刘宇才2");
System.out.println(map); //{1=刘宇才2, 2=邓雪绸}
System.out.println(map.get(1)); //刘宇才2
}
}
六.put（）方法
public V put(K key, V value) {
Entry<K,V> t = root;
/**
* 如果根节点都为null，表示还没建立起来红黑树，则通过new Entry（）
* 来创建根节点
*/
if (t == null) {
compare(key, key); // type (and possibly null) check 即：键入（可能为null）检查 即：检查节点的key是否为NUll
root = new Entry<>(key, value, null); //创建根节点
size = 1; //红黑树的节点数量为1
modCount++; //修改次数加1
return null;
}
int cmp; //如果节点不为null,定义一个cmp，存放比较的结果
Entry<K,V> parent; //定义parent，是new Entry时必须要的参数
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) { //表示用户自定义了比较器comparator
do {
parent = t;
/*
*调用比较器cpr的compare()方法比较parent 的key和要插入节点的key
*如果key为null时，compare(key, t.key)里面会报错
*/
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else //key相同，则更改节点的值
return t.setValue(value);
} while (t != null);
}
else { //表示用户自默认比较器comparator，TreeMap中的key对象都要实现Comparable接口，并重写compareTo()方法
if (key == null) //key值是不能为null的
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
/*
* 能执行到这里，说明前面并没有找到相同的key,节点已经遍历到最后了,
* 我们只需要new一个Entry放到parent下面即可，但放到左子节点上还是右子节
* 点上，就需要按照红黑树的规则来。
*/
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
/**
* 节点加进去了，并不算完，我们在前面红黑树原理章节提到过，一般情况下加入
* 节点都会对红黑树的结构造成破坏，我们需要通过一些操作来进行自动平衡处置
* 如【变色】【左旋】【右旋】
*/
fixAfterInsertion(e); //调整红黑树
size++;
modCount++;
return null;
}
上面put()代码中， compare(key, key)和cmp = cpr.compare(key, t.key);中compare()方法用来判断key是否为null。如果为null则会报错，这就体现了，TreeMap中的key不能为null,以及TreeMap中key类型必须为引用类型
/**
* 使用此TreeMap的正确比较方法比较两个键。
* 如果key为null时，(Comparable)k1).compareTo((K)k2)
* 和comparator.compare((K)k1, (K)k2)就会报错，
*/
@SuppressWarnings("unchecked")
final int compare(Object k1, Object k2) {
return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2)
: comparator.compare((K)k1, (K)k2);
}
红黑树规则特点：
- 节点分为红色或者黑色；
- 根节点必为黑色；
- 叶子节点都为黑色，且为null；
- 连接红色节点的两个子节点都为黑色（红黑树不会出现相邻的红色节点）；即：若一个节点为红色，则其父节点为黑色（重要）
- 从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点（每个节点的黑高相同；
- 新加入到红黑树的节点为红色节点；
/** From CLR */
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //先把新增的节点变为红色，对应特点6
//如果新增节点为 根节点 或者 父节点为红色，则新增节点变为 黑色 即可
while (x != null && x != root && x.parent.color == RED) {
//如果新增节点的 父节点 为 爷爷的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//y为新增节点的 右叔叔 节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { //如果右叔叔为红色
setColor(parentOf(x), BLACK); //把父节点变为黑色
setColor(y, BLACK); //把右叔叔节点变为黑色
setColor(parentOf(parentOf(x)), RED); //把爷爷节点变为红色，由特点四得之前为黑色
x = parentOf(parentOf(x)); //x变为爷爷节点
} else { //如果右叔叔为黑色
//如果单前节点为 右孩子节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x); //单前节点为父节点
rotateLeft(x); //左旋
}
setColor(parentOf(x), BLACK); //设置父节点为黑色
setColor(parentOf(parentOf(x)), RED); //设置爷爷节点为红色
rotateRight(parentOf(parentOf(x))); //对爷爷节点右旋
}
} else { //如果新增节点的 父节点 为 爷爷的右孩子节点
//y为新增节点的 左叔叔 节点
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) { //如果左叔叔为红色
setColor(parentOf(x), BLACK); //把父节点变为黑色
setColor(y, BLACK); //把左叔叔节点变为黑色
setColor(parentOf(parentOf(x)), RED); //把爷爷节点变为红色
x = parentOf(parentOf(x)); //x变为爷爷节点
} else { //如果左叔叔为黑色
//如果单前节点为 左孩子节点
if (x == leftOf(parentOf(x))) {
x = parentOf(x); //单前节点为父节点
rotateRight(x); //右旋
}
setColor(parentOf(x), BLACK); //设置父节点为黑色
setColor(parentOf(parentOf(x)), RED); //设置爷爷节点为红色
rotateLeft(parentOf(parentOf(x))); //对爷爷节点左旋
}
}
}
root.color = BLACK;
}
先了解下左旋和右旋：
 |
 |
|---|---|
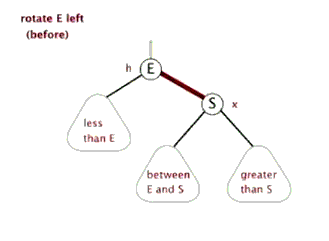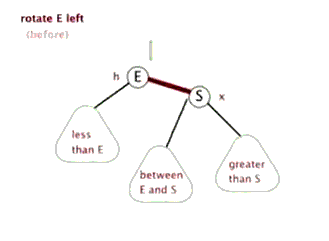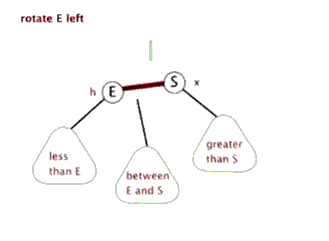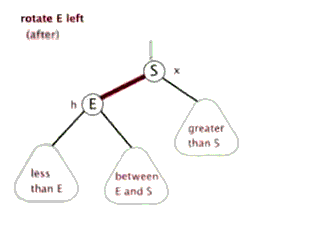| 左旋 | 右旋 |
（图片来自：http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html）
/** 左旋 */
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right; //r为单前节点的右孩子
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
/** 右旋 */
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
左旋过程图片：
put()流程图：
case1: y为右叔叔，且y为红色
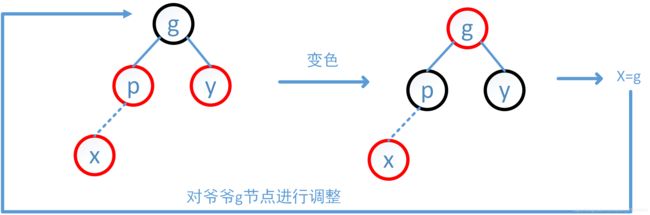
解决：p、y染黑，g染红。由于g原本为黑，黑 ——>红 可能会对g的上面结构进行破坏，此时要对g进行调整。
case2: y为右叔叔，且y为黑色
case2-1: x为右孩子
解决：先把x指向父节点，再对父节点x进行左旋，通过染色，p(x) 红——>黑，
g 黑——>红， g右旋。 由于调整后g——>P(x),颜色不发生改变，故对P(x)上面的结构没有造成破坏。
case2-2: x为左孩子
解决：先变色，p 红——>黑，g 黑——>红， g右旋。 由于调整后g——>P,颜色不发生改变，故对P上面的结构没有造成破坏。
分析： 通过case2-1和case2-2的图发现，case2-2是case2-1图的一部分。可以得出，当x为右孩子时，先左旋变为x为左孩子的情况，再做进一步的调整。
case3: y为左叔叔，且y为红色
解决：p、y染黑，g染红。由于g原本为黑，黑 ——>红 可能会对g的上面结构进行破坏，此时要对g进行调整。
case4: y为左叔叔，且y为黑色
case4-1: x为右孩子
解决：先变色，p 红——>黑，g 黑——>红， g左旋。 由于调整后g——>P,颜色不发生改变，故对P上面的结构没有造成破坏。
case4-2: x为左孩子
解决：先把x指向父节点，再对父节点x进行右旋，通过染色，p(x) 红——>黑，g 黑——>红， g左旋。 由于调整后g——>P(x),颜色不发生改变，故对P(x)上面的结构没有造成破坏。
分析： 通过case4-1和case4-2的图发现，case4-1是case4-2图的一部分。可以得出，当x为左孩子时，先右旋变为x为右孩子的情况，再做进一步的调整。
总结: 在最后一次旋转节点时，Y黑情况，口诀
y右黑 x左 g右旋；
y左黑 x右 g左旋；
七.get（）方法
get方法是通过二分查找的思想，我们看一下源码
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
if (comparator != null) //如果自定义了比较器，通过下面方法用自定义比较器查找
return getEntryUsingComparator(key);
if (key == null) //key不能为null
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
/**
*用自定义比较器查找
*/
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator<? super K> cpr = comparator;
if (cpr != null) {
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}
八.remove（）方法
remove方法可以分为两个步骤：
- 先是调用了上面介绍的getEntry(Object key)方法找到要删除的节点
- 找到删除的节点后的调用deleteEntry§方法执行删除操作。
public V remove(Object key) {
Entry<K,V> p = getEntry(key); //找到要删除的节点
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p); //删除节点，
return oldValue;
}
deleteEntry§执行删除节点时分为两个步骤：
- 删除节点
- 调整红黑树（由于删除节点后可能会对红黑树的平衡结构进行破坏）
通过deleteEntry§进行删除操作的原理：
- 删除的是根节点，则直接将根节点置为null;
- 待删除节点的左右子节点都为null，删除时将该节点置为null;
- 待删除节点的左右子节点有一个有值，则用有值的节点替换该节点即可；
- 待删除节点的左右子节点都不为null，则找前驱或者后继，将前驱或者后继的值复制到该节点中，然后删除前驱或者后继（前驱：左子树中值最大的节点，后继**：右子树中值最小的节点**）；
/**
* Delete node p, and then rebalance the tree.
* 翻译：删除节点p，然后重新平衡树。
*/
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// point to successor.即：指向继任者。
if (p.left != null && p.right != null) { //如果删除的节点有左右孩子
Entry<K,V> s = successor(p); //通过successor(p)遍历红黑树找到前驱或者后继
/*
*找到前驱和后继节点s后
*将前驱或者后继的key和value复制到当前节点p中
*然后删除节点s(通过将节点p引用指向s)
*/
p.key = s.key;
p.value = s.value;
p = s;
}
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
//如果至少有一个左右孩子
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null) //如果该节点是根节点
root = replacement; //把replacement作为根节点
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
/**
* p如果是红色节点的话，那么其子节点replacement必然为红色的，并不影响红黑树的结构。
* 但如果p为黑色节点的话，那么其父节点以及子节点都可能是红色的，
* 那么很明显可能会存在红色相连的情况，因此需要进行自平衡的调整
*/
if (p.color == BLACK)
fixAfterDeletion(replacement); //调整红黑树
} else if (p.parent == null) { //说明没有左右孩子且没有父节点
root = null; //说明该节点是根节点且红黑树只有这一个节点
} else { //没有左右孩子
/**
* 如果p节点为黑色，那么p节点删除后，就可能违背每个节点到其叶子节点
* 路径上黑色节点数量一致的规则，因此需要进行自平衡的调整
*/
if (p.color == BLACK)
fixAfterDeletion(p);
//把该节点的父节点指向该节点的引用为空
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
/**
* Returns the successor of the specified Entry, or null if no such.
* 翻译：返回指定Entry的后继者，如果不是，则返回null。
* 如果要删除的节点有的右孩子有左子树，则返回左子树中最小的节点
* 如果没有左子树，则返回左孩子
*/
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { //删除操作这部分代码没有用到，不解释
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
case1: 删除的节点有左右孩子
解决：如果删除的节点p有左右子节点，如果右子节点中有左子树，则找出右子节点的左子树的最小节点s，如果右子节点没有左子树，则找该右子节点为s；接着把s的key和value值赋给要删除的节点p。如果s有左右子节点（此时s只有右节点，由于s已是最左侧的最小的了），则把s的右节点作为s父节点的子节点。
**注意：**还没结束，由于要删除的节点在结构上并不是真正的删除目标节点，而是把另一个节点的key和value赋值给该节点，而删除的是另一节点即s节点，目标节点的颜色没有改变。如果s的节点是黑色，可能会违法红黑树的特点5，即：从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点。此时要对s的右子节点replacement 进行调整。
case2: 删除的节点有左孩子，没右孩子
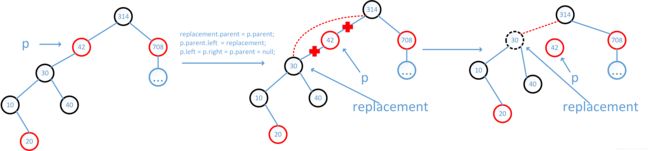解决：要删除的节点p只有左孩子，则把该左孩子replacement作为p节点的父节点的左孩子节点。
注意： 由于要删除的节点p如果颜色为黑色，删除后，可能会违法红黑树的特点5，即：从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点。此时要对p的左子节点replacement 进行调整（此时的P没有右子节点的）。
case3: 删除的节点有右孩子，没左孩子
解决：要删除的节点p只有右孩子，则把该右孩子replacement作为p节点的父节点的左孩子节点。
注意： 由于要删除的节点p如果颜色为黑色，删除后，可能会违法红黑树的特点5，即：从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点。此时要对p的右子节点replacement 进行调整（此时的P没有左子节点的）。
参考： https://www.cnblogs.com/LiaHon/p/11221634.html