java实现二叉树的Node节点定义,并手撕8种遍历

最近准备秋招面试，发现二叉树这种可以无限扩展知识点来虐别人的数据结构，很受面试官的青睐。

如果掌握的不好，会直接死在一面哦。

怕吗？当你原理、思想，内部结构通通明白，分分钟手撕代码的程度，还怕吗？

本篇文章就从用java的思想和程序从最基本的怎么将一个int型的数组变成Node树状结构说起，再到递归前序遍历，递归中序遍历，递归后序遍历，非递归前序遍历，非递归前序遍历，非递归前序遍历，到最后的广度优先遍历和深度优先遍历

来咯！

---

一、Node节点的java实现

首先在可以看到打上Node这个字符串，就可以看到只能的IDEA系统提供的好多提示：

点进去看，却不是可以直接构成二叉树的Node，不是我们需要的东西。这里举个例子来看
org.w3c.dom
这里面的Node是一个接口，是解析XML时的文档树。在官方文档里面看出：该 Node 接口是整个文档对象模型的主要数据类型。它表示该文档树中的单个节点。当实现 Node 接口的所有对象公开处理子节点的方法时，不是实现 Node 接口的所有对象都有子节点。

所以我们需要自定义一个Node类

package com.sort.text;

public class Node {
	private int value;        //节点的值
	private Node node;        //此节点，数据类型为Node
	private Node left;        //此节点的左子节点，数据类型为Node
	private Node right;       //此节点的右子节点，数据类型为Node
	
	public int getValue() {
		return value;
	}

	public void setValue(int value) {
		this.value = value;
	}

	public Node getNode() {
		return node;
	}

	public void setNode(Node node) {
		this.node = node;
	}

	public Node getLeft() {
		return left;
	}

	public void setLeft(Node left) {
		this.left = left;
	}

	public Node getRight() {
		return right;
	}

	public void setRight(Node right) {
		this.right = right;
	}

	public Node(int value) {
		this.value=value;
		this.left=null;
		this.right=null;
	}
	public String toString() {         //自定义的toString方法，为了方便之后的输出
		return this.value+" ";
	}
}

定义好了之后就可以开始直接使用了，相信大家都可以秒看懂。

二、数组升华二叉树

一般拿到的数据是一个int型的数组，那怎么将这个数组变成我们可以直接操作的树结构呢？

1、数组元素变Node类型节点
2、给N/2-1个节点设置子节点
3、给最后一个节点设置子节点【有可能只有左节点】

那现在就直接上代码

public  static void create(int[] datas,List list) {

		//将数组里面的东西变成节点的形式
		for(int i=0;i

很细致的加上了很多的注释啊，所以保证一看就懂。
开始大招前的攒金币过程正式结束
现在开始放大招

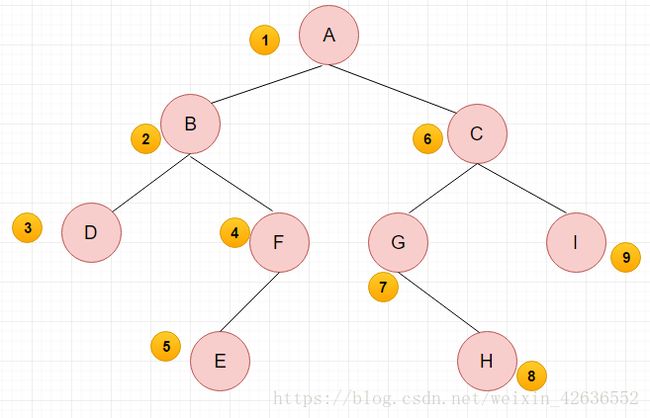
三、递归前序遍历

具体的原理没有什么好讲的，知道顺序即可

先序遍历过程：
（1）访问根节点；
（2）采用先序递归遍历左子树；
（3）采用先序递归遍历右子树；

这里用图来说明

先序遍历结果：A BDFE CGHI

还是看代码吧

 public void preTraversal(Node node){
       if (node == null) //很重要，必须加上 当遇到叶子节点用来停止向下遍历
             return; 
         System.out.print(node.getValue()+" ");
        preTraversal(node.getLeft());
        preTraversal(node.getRight());
 }

看，说了很简单吧！

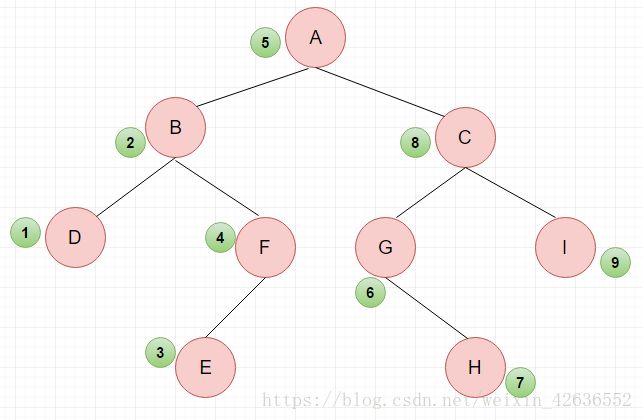
四、递归中序遍历

中序遍历：
（1）采用中序遍历左子树；
（2）访问根节点；
（3）采用中序遍历右子树

中序遍历结果：DBEF A GHCI

有请代码：

public void    MidTraversal(Node node){
      if (node == null)
          return; 
     MidTraversa(node.getLeft());
     System.out.print(node.getValue()+" ");
     MidTraversa(node.getRight());
 }

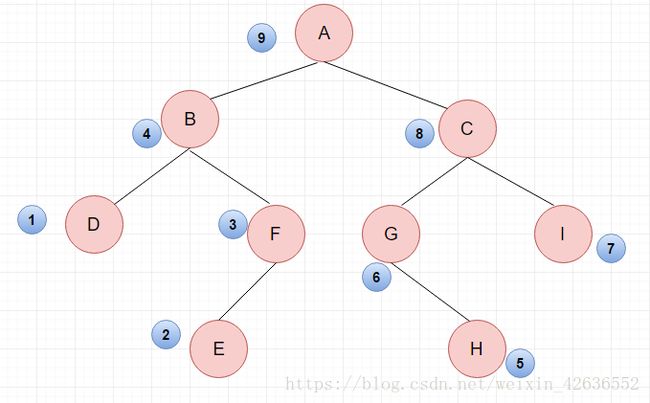
五、递归后序遍历

后序遍历：
（1）采用后序递归遍历左子树；
（2）采用后序递归遍历右子树；
（3）访问根节点；

后序遍历的结果：DEFB HGIC A

代码：

 public void postTraversal(Node node){
         if (node == null) 
                 return; 
         postTraversal(node.getLeft());
        postTraversal(node.getRight());
        System.out.print(node.getValue()+" ");
 }

其实代码和思想一样，只是输出的位置和递归调用的位置不同而已。

个人觉得懂得非递归的原理和代码比懂递归更有意思，当你能手撕非递归二叉树遍历的时候，面试官问你原理，还能不知道吗？

那接下来的三个模块就是非递归的三种遍历

拭目以待

六、非递归前序遍历

我这里使用了栈这个数据结构，用来保存不到遍历过但是没有遍历完全的父节点
之后再进行回滚。

基本的原理就是当循环中的p不为空时，就读取p的值，并不断更新p为其左子节点，即不断读取左子节点，直到一个枝节到达最后的子节点，再继续返回上一层进行取值

代码：

public void preOrderTraversalbyLoop(Node node){
          Stack stack = new Stack();
          Node p = node;
          while(p!=null || !stack.isEmpty()){
                 while(p!=null){ 
                 //当p不为空时，就读取p的值，并不断更新p为其左子节点，即不断读取左子节点
                   System.out.print(p.getValue()+" ");
                   stack.push(p); //将p入栈
                   p = p.getLeft(); 
               }
              if(!stack.isEmpty()){
               p = stack.pop();
               p = p.getRight();
             }
        }
 }

执行结果，很顺利的得到想要的结果

七、非递归中序遍历

同原理

就是当循环中的p不为空时，就读取p的值，并不断更新p为其左子节点，但是切记这个时候不能进行输出，必须不断读取左子节点，直到一个枝节到达最后的子节点，然后每次从栈中拿出一个元素，就进行输出，再继续返回上一层进行取值

代码如下：

public void inOrderTraversalbyLoop(Node node){
         Stack stack = new Stack();
         Node p = node;
         while(p!=null || !stack.isEmpty()){
            while(p!=null){
               stack.push(p);
               p = p.getLeft();
          }
           if(!stack.isEmpty()){ 
                  p = stack.pop();
                     System.out.print(p.getValue()+" ");
                 p = p.getRight();
            }
      }
 }

八、非递归后序遍历

后序遍历相比前面的前序遍历和中序遍历在编程这里会难一点，不过理解了思想，看代码还是没有什么问题的

 public void postOrderTraversalbyLoop(Node node){

          Stack stack = new Stack();
         Node p = node,    prev = node;
         while(p!=null || !stack.isEmpty()){
                while(p!=null){
                     stack.push(p);
                     p = p.getLeft();
              }
               if(!stack.isEmpty()){
                     Node temp = stack.peek().getRight();
                     //只是拿出来栈顶这个值，并没有进行删除
                     if(temp == null||temp == prev){
                       //节点没有右子节点或者到达根节点【考虑到最后一种情况】
                        p = stack.pop();
                       System.out.print(p.getValue()+" ");
                       prev = p;
                       p = null;
                       }
                       else{
                                p = temp;
                                } 
                 }
       }
 }

最后就可以放大招了，来看看广度优先遍历和深度优先遍历吧

九、广度优先遍历

 public void bfs(Node root){
  if(root == null) return;
  LinkedList queue = new LinkedList();
  queue.offer(root); //首先将根节点存入队列
  //当队列里有值时，每次取出队首的node打印，打印之后判断node是否有子节点，若有，则将子节点加入队列
  while(queue.size() > 0){ 
  Node node = queue.peek();
   queue.poll(); //取出队首元素并打印
   System.out.print(node.var+" ");
   if(node.left != null){ //如果有左子节点，则将其存入队列
    queue.offer(node.left);
   }
   if(node.right != null){ //如果有右子节点，则将其存入队列
    queue.offer(node.right);
   }
  }
 }

九、深度优先遍历

public void dfs(Node node,List> rst,List list){
 if(node == null) return;
 if(node.left == null && node.right == null){
  list.add(node.var);
  /* 这里将list存入rst中时，不能直接将list存入，而是通过新建一个list来实现，
  * 因为如果直接用list的话，后面remove的时候也会将其最后一个存的节点删掉
  * */
  rst.add(new ArrayList<>(list));
  list.remove(list.size()-1);
 }
 list.add(node.var);
 dfs(node.left,rst,list);
 dfs(node.right,rst,list);
 list.remove(list.size()-1);
 }

------------------------------------------------------未完待续哦-----------------------------