图论——最大团问题和最大独立集、二分图相关
文章目录
- 最大团问题和最大独立集
- 二分图、用网络流解决最大二分匹配的方法
- 一种另类的增广路——交替路、匈牙利算法
- 一般图、二分图中的其它性质
- P1640 [SCOI2010]连续攻击游戏
最大团问题和最大独立集
最大团的定义:
设一个无向图 G ( V , E ) G(V,E) G(V,E), V V V为点集, E E E为两点间的边集。设 U U U为 V V V的一个子集,若对于任意的结点对 u u u, v v v属于 U U U都有边连通,则称点集U构成的图为 完全子图 。无向图 G G G的完全子图 U U U是 G G G的团, G G G的最大团即为 G G G的最大完全子图。

众所周知,最大团问题是一个NP完全问题,有很多求解它的 名字中二而且牛逼的 算法,此处一概不叙述。

独立集:
图 G ( V , E ) G(V,E) G(V,E)中互不相邻的点构成的集合为独立集。
最大团与最大独立集的关系:
求解一个图中的最大独立街等价于求解其补图的最大团。
独立集的条件是任意两个点互不连通,那么如果把原图中连通的点之间的边删除,不连通点连接,即转化为求个数最多的两两连通点集,也即求最大团。
用DFS+剪枝,实现的求最大团的算法。
P1692 最大团模板
#include二分图、用网络流解决最大二分匹配的方法
二分图
设图 G ( V , E ) G(V,E) G(V,E)是一个无向图,如果图 G G G中的点可以划分为两个没有交集的点集 V 1 V1 V1和 V 2 V2 V2,并且每条边的两个端点分别在这个两个点集中,则称这样的图 G G G为一个二分图。
二分匹配:
给定一个二分图 G ( V , E ) G(V,E) G(V,E),对于它的一个子图 M M M,如果 M M M中任意的两条边都不连接同一个端点,则称 M M M为一个匹配。
最大二分匹配,要求 M M M中包括的点最多。
二分匹配与网络流的关系:
在二分匹配中,我们规定所有点集 V 1 V1 V1连向的边都指向点集 V 2 V2 V2,这样就能在不改变二分匹配性质的基础上转化为一个有向图。由于匹配的两个结点完全占用一条边,所以不妨设所有边的 “ 容量 ” 都为1。二分图显然是一个多源点、多汇点的图,但是并没有要求必须由哪个源点和哪个汇点一定要匹配。因此,可以考虑缩点,把所有源点合并,所有汇点合并。而这在网络流问题中有一个很好用的技巧,就是建立超级源点和超级汇点。建立一组边关系,超级源点 s s s指向点集 V 1 V1 V1中所有的点;同理,使点集 V 2 V2 V2中所有的点都有指向超级汇点 t t t的边。为了符合二分匹配的性质,要求这些新增的边的权值都为1。处理最大二分匹配的问题即转化为计算最大流的问题(或者说寻找所有的增广路径),只不过,每一次增加的流大小只能是1,当没有增广路径的同时,答案也就显然了。

不清楚网络流的同学可以看这一篇博客图论——最大流的增广路相关算法
参考模板题:P3386 【模板】二分图匹配
这一百来行dinic算法的运行效率(两个点集的点数各小于等于1000):

Code
#include一种另类的增广路——交替路、匈牙利算法
交替路:
通过上面对dinic算法的分析,很明显可以看出,使用网络流算法解决二分匹配问题是没有必要的。就像处理边权为1的单源最短路径,没有必要使用dijkstra算法。网络流中寻找增广路以及建立反向边的操作实际是在浪费时间,完全可以用 交替路 处理。交替路适用于无向图,从一个为匹配点出发,一次走未匹配边、匹配边、未匹配边…直到遇到未匹配点,这样就构建出一条增广路径,沿着这条增广路径,对边的性质取反。
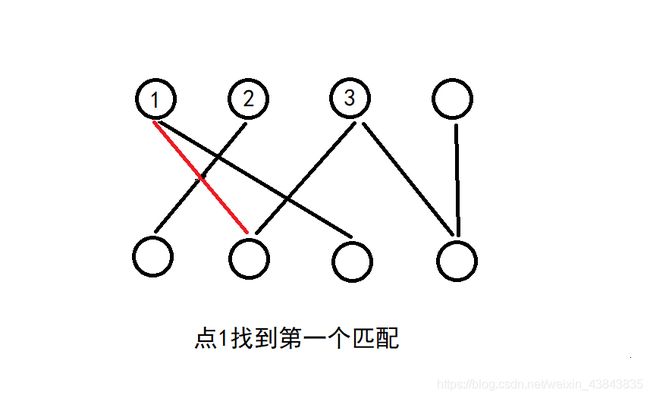

匈牙利算法:
寻找交替路是匈牙利算法的核心,每找到一次增广路,对边进行反转,当某个点集遍历完一遍没有新的增广路时,算法终止,此时满足最大二分匹配。以下证明一下匈牙利算法的正确性:
定理一:满足最大匹配的充要条件是没有新的增广路
按照增广路的选取规则,每次选择的路径都是按未匹配、匹配、未匹配的规则进行,每一次增广都会增加一个匹配。假设图 G ( V , E ) G(V,E) G(V,E)此时满足最大匹配,显然匹配数已经无法增加,所以增广路必然不存在。如果一个图不满足最大匹配,就一定能找到一个新的匹配,也即一定会有一条新的增广路径。(和网络流中增广路性质等同)
定理二:如果某一个点没有新的增广路,那么后面的点的增广路径与该点无关。
假设某一个点 u u u没有新的增广路径,而后面某一个点 u ′ u' u′的增广路径经过了 u u u,那就说明在这之前的某一个结点一定也存在一条相对短的增广路径经过 u u u。同时可以推出,如果没有新的结点加入,而且最后一个点也没有新的增广路径,那么整个图就没有增广路径,所以,匈牙利算法中只要对其中一个点集遍历一遍,就能找到最大二分匹配。
匈牙利算法的实现,可以基于DFS或BFS,下面是一个DFS的版本。
P3386 【模板】二分图匹配
Code
#include一般图、二分图中的其它性质
最小边覆盖:
边覆盖指图 G ( V , E ) G(V,E) G(V,E)中的一个边子集,满足图上的每一个结点都与这个边集合关联。
最小边覆盖中,这个边子集包含的边数最少。
最小点覆盖:
点覆盖值图 G ( V , E ) G(V,E) G(V,E)中的一个点子集,满足图中的每一个边都与这个点集合关联。
最小点覆盖中,这个点子集包含的点数最少。
对于一个连通图:最大匹配+最小边覆盖=结点数
最大独立集+最小顶点覆盖=结点数
二分图中:最小顶点覆盖=最大二分匹配
P1640 [SCOI2010]连续攻击游戏
——题解——
做一道最大二分匹配的题目练练手。本题有两个思路,一个是对装备进行匹配,一个是对属性进行匹配。但是,题目要求,攻击必须满足属性值连续且递增,所以不妨对属性进行匹配。当存在某个属性不存在或无法被匹配时,即可得出符合题意的最大匹配度。
——Code——
#include