线段树求解各种问题的模板(单点修改、区间修改、扫描线思想)
文章目录
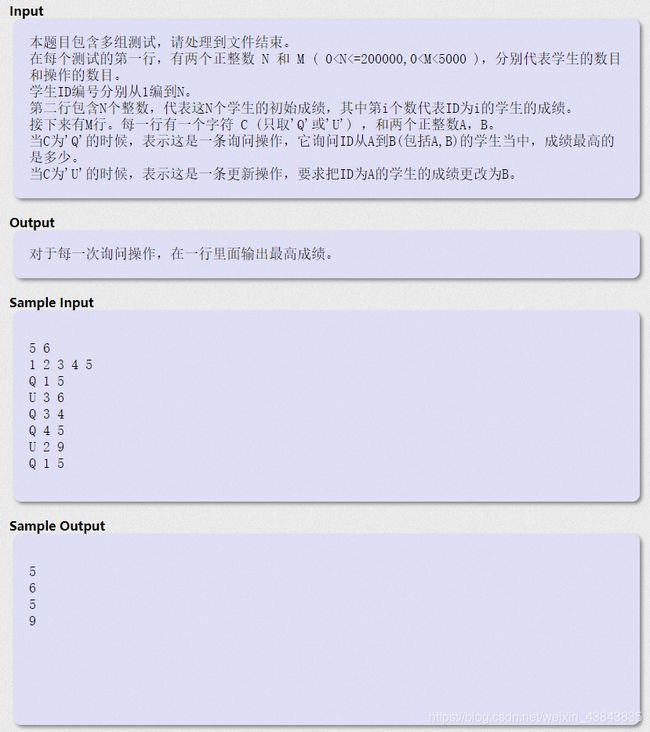
- 单点修改
- 区间求和
- 区间最值
- 求逆序对
- 求区间最大位子
- 区间修改
- 成段替换
- 成段增减区间求和
- 成段替换简单hash
- 区间合并
- 扫描线
- 矩形面积并
- 矩形周长并
这篇博客的基础: 线段树(简单实现高效区间操作)
单点修改
线段树的单点修改可以看成一个完整线段树的简化版,它的修改方式相当于在树状数组的基础上附带一个递归到需要修改的点的过程,所以效率略低于树状数组。
理解区间修改、区间最值及求和的原理后,单点更新的求和及最值问题就直接贴模板了。
区间求和
#include区间最值
#include求逆序对
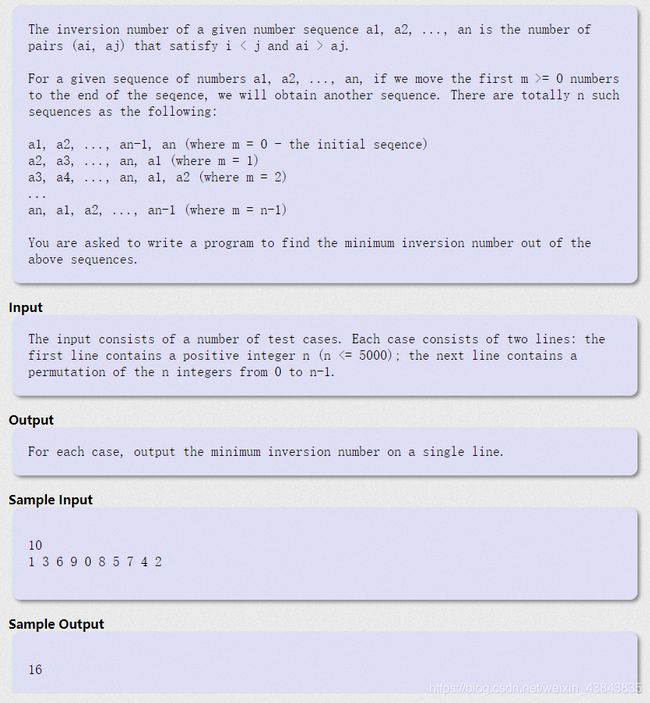
——题解——
出现过的数字标记为1,未出现的记为0,。我们维护的线段树相当于区间求和,每读入一个数字i,就对区间i~n求一次和,然后把i的位置标记为1
——Code——
#include求区间最大位子


——题解——
这题的意思是不断从左往右寻找能贴海报的位置,需要用一个线段树维护某段区间中最大的空余位置或最小的利用位置。
——Code——
#include区间修改
关于区间修改的问题我在上一篇博客中已经详细说明,下面的一些问题基本是模板或者是模板的简单变形。
成段替换
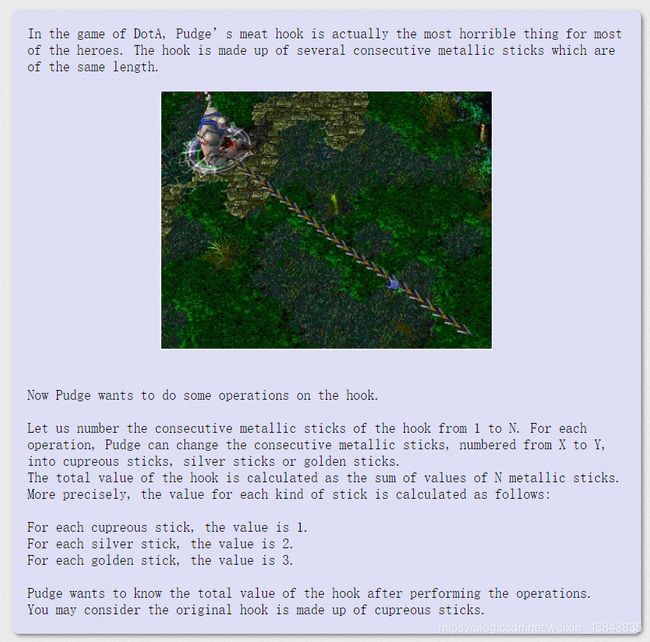

——题解——
在这题中lazytag充当区间属性的作用(即标记1、2、3),线段树维护区间和,答案就是线段树根节点的值。需要注意的是,当初始lazytag值为0时,千万不要向下传导lazytag。
——Code——
#include成段增减区间求和
——题解——
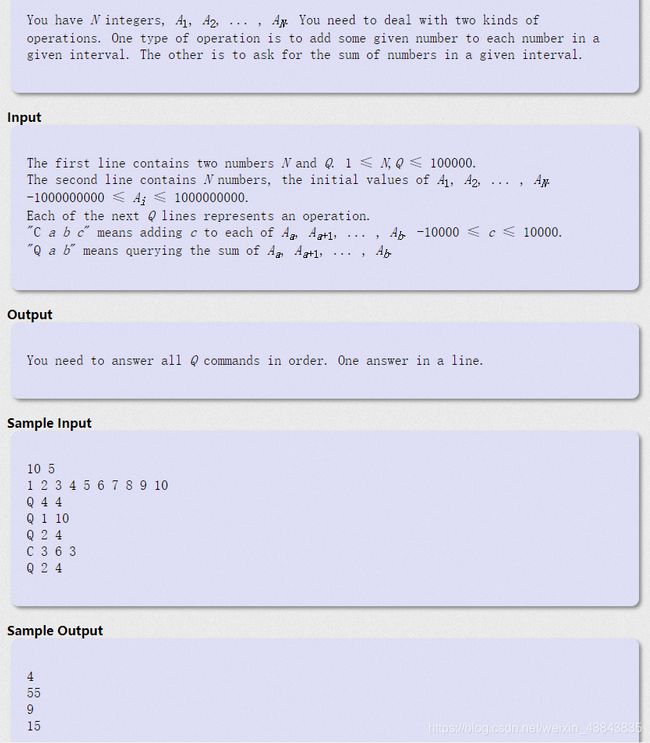
这是一道完整的线段树模板题,涵盖的线段树所有的操作,包括:建树、区间修改、lazytag传导、区间查询
——Code——
#include成段替换简单hash

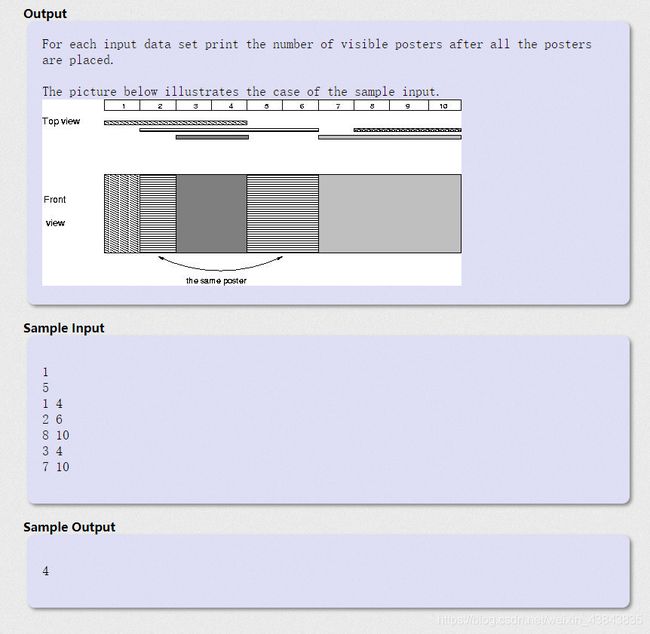
——题解——
这题是成段替换的一个变式,首先要对海报的区间进行离散化,然后从最后一张海报开始贴,如果能贴上,则返回bool值true,答案数加1
——Code——
#include 区间合并


——题解——
这是一道进阶的线段树题。线段树需要维护的是区间最大空余位置,考虑到有可能某连续空区间正好卡在两段自区间之间,所以线段树的维护需要三个值:从左端开始的连续空区间长度lv、从右端开始的连续空区间长度rv、最大空区间长度mv。对于一个区间来讲,它的lv即为左子区间的lv,rv即为右子区间的rv,中间空余区间长度即为左子区间的rv加上右子区间的lv,而mv即为三者中的最大值。
——Code——
#include
}else{
int x;
int d;
scanf("%d %d",&x,&d);
update(x,x+d-1,1,n,1,1);
}
}
}
return 0;
}
扫描线
关于扫面线的讲解,我推荐这篇博客扫描线+线段树
接下去的两题都是上面这篇博客的例题,所以我直接贴代码了。
矩形面积并
——Code——
#include
int length = unique(x+1,x+cntline+1)-x-1;//离散化,去掉重复的端点
double ans=0;
for(int i=1;i<=cntline;++i)
{
int lq = binary(length,seg[i].l)+1;
int rq = binary(length,seg[i].r);
update(lq,rq,1,length,1,seg[i].d);
ans+=(seg[i+1].h-seg[i].h) * tree[1];
// cout<
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",now,ans);
}
return 0;
}
矩形周长并
#include