noip 2002 普及组 T4 过河卒

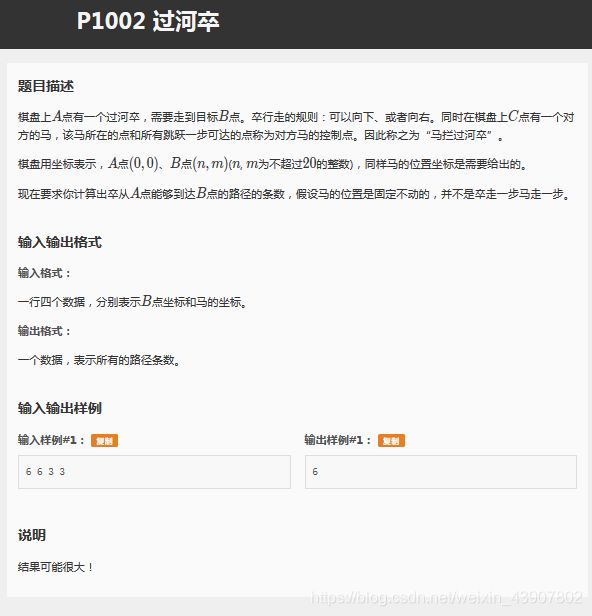
题面

分析

乍一看，水题！深搜秒掉！好的，最多最多60pts lol
为什么呢？说明中说：结果可能很大！
dfs只有走向爆栈
正解是DP
由于兵只可以向上或右走，于是设f[x][y]是位置为（x，y）的点到点（n，m）的所有路径，据加法原理有
$f[x][y]=f[x-1][y]+f[x][y-1]$

code

DFS(luogu 40pts)

#include
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;i++)
#define clean(arry,num); memset(arry,num,sizeof(arry));
#define max(a,b) (a>b)?a:b;
#define min(a,b) (a
#define printG(); loop(i,0,20){loop(j,0,20)printf("%3.d ",(g[i][j]==0)?9:g[i][j]);printf("\n");}
int n,m,m_x,m_y;//ans=0;
const int maxn=25;
const int maxm=25;
int g[maxn][maxm];
bool vis[maxn][maxm];
int dx[2]={0,1};
int dy[2]={1,0};
int dx2[8]={2,-2,2,-2,-1,1,-1,1},dy2[8]={1,1,-1,-1,2,2,-2,-2};
inline int read()
{
    int ans=0;char r=getchar();bool neg=false;
    while(r>'9'||r<'0'){if(r=='-')neg=true;r=getchar();}
    while(r>='0'&&r<='9'){ans=ans*10+r-'0';r=getchar();}
    return ans;
}
void datasetting()
{
    clean(g,0);
    n=read();m=read();m_x=read();m_y=read();
    n++;m++;m_x++;m_y++;
    clean(g[0],-1);clean(g[n+1],-1);
    loop(i,0,n+1)g[i][0]=g[i][m+1]=-1;
    g[m_x][m_y]=-1;
    loop(i,0,7)if(m_x+dx2[i]>0&&m_x+dx2[i]<n+1&&m_y+dy2[i]>0&&m_y+dy2[i]<m+1)g[m_x+dx2[i]][m_y+dy2[i]]=-1;//
    //printG();
}
int dfs(int x,int y)
{
    //printf("%d %d\n",x,y);
    if(x==n&&y==m)return 1;
    int ans=0;
    loop(i,0,1)
    {
        int nx=x+dx[i];
        int ny=y+dy[i];
        if(g[nx][ny]==-1||vis[nx][ny])continue;
        //printf("%d %d\n",nx,ny);
        vis[nx][ny]=true;
        ans+=dfs(nx,ny);
        vis[nx][ny]=false;
    }
    return ans;
}
int main()
{
    //freopen("datain.txt","r",stdin);
    //freopen("dataout.txt","w",stdout);
    clean(vis,false);
    datasetting();
    vis[1][1]=true;
    printf("%d",dfs(1,1));
    return 0;
}

DP

#include
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;i++)
#define clean(arry,num); memset(arry,num,sizeof(arry));
#define max(a,b) (a>b)?a:b;
#define min(a,b) (a
#define printG(); loop(i,0,24){loop(j,0,24)printf("%9.d",f[i][j]/*(f[i][j]==0)?-2:f[i][j]*/);printf("\n");}printf("\n");
#define clear(a) ((a==-1)?0:a)//防止马控制区的标记对dp的影响
#define ll long long
const int maxn=25,maxm=25;
ll f[maxn][maxm];
int dx2[8]={2,-2,2,-2,-1,1,-1,1},dy2[8]={1,1,-1,-1,2,2,-2,-2};
int n,m,m_x,m_y;
inline int read()
{
    int ans=0;char r=getchar();
    while(r>'9'||r<'0')r=getchar();
    while(r>='0'&&r<='9'){ans=ans*10+r-'0';r=getchar();}
    return ans;
}
int main()
{
    n=read()+1;m=read()+1;m_x=read()+1;m_y=read()+1;
    clean(f,0);
    f[m_x][m_y]=-1;
    loop(i,0,7)if(m_x+dx2[i]>0&&m_x+dx2[i]<n+1&&m_y+dy2[i]>0&&m_y+dy2[i]<m+1)f[m_x+dx2[i]][m_y+dy2[i]]=-1;//
    f[n][m]=1;
    for(int i=n;i>=1;i--)
    {
        for(int j=m;j>=1;j--)//这里的顺序根据实际情况调整了一下
        {
            if(f[i][j]==-1)continue;
            f[i][j]+=clear(f[i+1][j])+clear(f[i][j+1]);
        }
    }
    printf("%lld",f[1][1]);
    return 0;
}

学到的东西

1.时间复杂度的估计
为什么dfs会TLE？
dfs实质是对二叉树的遍历，若不考虑玄学回溯的话，其时间复杂度是O(n),n是节点个数
而本题中，节点个数n有最大值为
$2^{20}+2^{19}+2^{18}+...+2^2+2^1+2^0$
这可是个天文数字，再加上出题人的精心设计（玄学复杂度的消失不见），呵呵呵

2.注意开long long