矩阵加速

目录

一.矩阵乘法

1.什么是矩阵乘法

2.矩阵乘法运算的规律

3.模板

二.矩阵加速

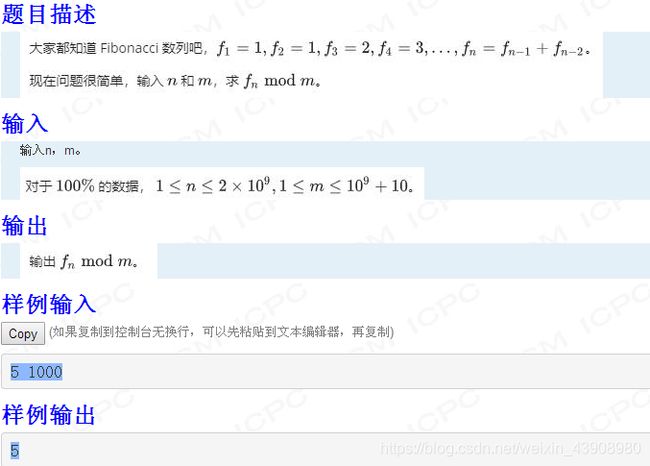
1.例1：Fibonacci 第 n 项

（1）题目

（2）题解

（3）代码

2.例2：Fibonacci前n项和

（1）题目

（2）题解

（3）代码

谢谢！

---

一.矩阵乘法

要想学会矩阵加速就要学会一个重头戏——矩阵乘法。

1.什么是矩阵乘法

矩阵乘法只有在第一个矩阵的列数等于第二个矩阵的行数的时候才能进行运作。

举个例子：

矩阵乘法就是拿第一个矩阵的第i行依次去乘第二个矩阵的每一列作为最终答案矩阵的第i行，最终答案矩阵的大小是取第一个矩阵的行数和第二个矩阵的列数，所以不一定是个方阵。

2.矩阵乘法运算的规律

矩阵乘法满足结合律、分配率，但是不满足交换律，用字母表示就是（A,B,C表示矩阵）：

，除非A和B矩阵都是方阵。

3.模板

//结构体模板，好用一些，不用传参
struct node {
    int n, m;
    LL jz[M][M];
    void Read (){
        scanf ("%d %d", &n, &m);
        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= m; j ++)
                scanf ("%lld", &jz[i][j]);
    }
    node operator * (const node& r) const{
        node ans;
        for (int i = 1; i <= n; i ++){
            for (int j = 1; j <= r.m; j ++){
                for (int k = 1; k <= r.n; k ++){
                    ans.jz[i][j] += jz[i][k] * r.jz[k][j];
                }
            }
        }
        ans.n = n;
        ans.m = r.m;
        return ans;
    }
    void print (){
        for (int i = 1; i <= n; i ++){
            for (int j = 1; j < m; j ++){
                printf ("%lld ", jz[i][j]);
            }
            printf ("%lld\n", jz[i][m]);
        }
    }
}A, B, C;

二.矩阵加速

矩阵加速说白了就是利用矩阵乘法来对算法进行一些十分神奇的加速。请看例题：

1.例1：Fibonacci 第 n 项

（1）题目

（2）题解

这道题如果用暴力的话绝对超时，所以我们的目标就是优化。

只有降到log级别的时间复杂度才能解决这道题，那么你想到了吗？矩阵快速幂！

那么，如何定义这两个矩阵呢？一个矩阵用来快速幂，一个矩阵用来计算结果。

公布答案：用来计算答案的矩阵A：，用来快速幂的矩阵B：

为什么呢？大家不妨来乘一乘：

啊，是不是很震惊，想要算直接用A乘就行了。

矩阵快速幂就是一般快速幂加矩阵乘法。

（3）代码

#include 
#include 
#include 
using namespace std;
#define LL long long
LL n, m;
struct node {
    LL r, c, jz[10][10];
    node operator * (const node& rhs) const{
        node ans;
        ans.r = r, ans.c = rhs.c;
        for (int i = 0; i <= 9; i ++)
            for (int j = 0; j <= 9; j ++)
                ans.jz[i][j] = 0;
        for (int i = 1; i <= r; i ++)
            for (int j = 1; j <= rhs.c; j ++)
                for (int k = 1; k <= c; k ++)
                    ans.jz[i][j] = (ans.jz[i][j] + jz[i][k] * rhs.jz[k][j] % m) % m;
        return ans;
    }
}A, B, C;
void prepare (node &ans){
    for (int i = 0; i <= 9; i ++)
        for (int j = 0; j <= 9; j ++)
            ans.jz[i][j] = 0;
}
node qkpow (node x, LL y){
    node ans;
    prepare (ans);
    ans.r = ans.c = 2;
    for (int i = 1; i <= ans.r; i ++)
        ans.jz[i][i] = 1;
    while (y > 0){
        if (y % 2 == 1)
            ans = ans * x;
        x = x * x;
        y /= 2;
    }
    return ans;
}
int main (){
    scanf ("%lld %lld", &n, &m);
    B.r = 2, B.c = 2;
    B.jz[1][1] = 0, B.jz[1][2] = B.jz[2][1] = B.jz[2][2] = 1;
    A.r = 1, A.c = 2;
    A.jz[1][1] = A.jz[1][2] = 1;
    A = A * qkpow (B, n - 2);
    printf ("%lld\n", A.jz[1][2]);
    return 0;
}

2.例2：Fibonacci前n项和

（1）题目

（2）题解

经过上一题的锻炼，我们已经掌握了如何求第n项，但是这次要求的是和。大家想到了吗？

我们模仿上一题，定义，自然B矩阵也要改成3*3。

我们的目标是，自然可以想到B为

然后和的变化模仿上一道题：

B矩阵就出来了，最后就又是一个矩阵快速幂的问题了。

（3）代码

#include 
#include 
#include 
using namespace std;
#define LL long long
LL n, m;
struct node {
    LL r, c, jz[10][10];
    node operator * (const node& rhs) const{
        node ans;
        ans.r = r, ans.c = rhs.c;
        for (int i = 0; i <= 9; i ++)
            for (int j = 0; j <= 9; j ++)
                ans.jz[i][j] = 0;
        for (int i = 1; i <= r; i ++)
            for (int j = 1; j <= rhs.c; j ++)
                for (int k = 1; k <= c; k ++)
                    ans.jz[i][j] = (ans.jz[i][j] + jz[i][k] * rhs.jz[k][j] % m) % m;
        return ans;
    }
}A, B, C;
void prepare (node &ans){
    for (int i = 0; i <= 9; i ++)
        for (int j = 0; j <= 9; j ++)
            ans.jz[i][j] = 0;
}
node qkpow (node x, LL y){
    node ans;
    prepare (ans);
    ans.r = ans.c = 3;
    for (int i = 1; i <= ans.r; i ++)
        ans.jz[i][i] = 1;
    while (y > 0){
        if (y % 2 == 1)
            ans = ans * x;
        x = x * x;
        y /= 2;
    }
    return ans;
}
int main (){
    scanf ("%lld %lld", &n, &m);
    B.r = 3, B.c = 3;
    B.jz[1][1] = B.jz[2][1] = B.jz[3][1] = B.jz[3][2] = B.jz[2][3] = B.jz[3][3] = 1;
    A.r = 1, A.c = 3;
    A.jz[1][3] = A.jz[1][2] = 1, A.jz[1][1] = 2;
    A = A * qkpow (B, n - 2);
    printf ("%lld\n", A.jz[1][1]);
    return 0;
}

谢谢！