图论--SPFA算法
算法优点:
1.时间复杂度比普通的Dijkstra和Ford低。
2.能够计算负权图问题。
3.能够判断是否有负环 (即:每跑一圈,路径会减小,所以会一直循环跑下去)。
算法思想:
我们用数组记录每个结点的最短路径估计值,用邻接表来存储图G。
我们采取的方法是动态逼近法:
1.设立一个先进先出的队列用来保存待优化的结点。
2.优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。
3.这样不断从队列中取出结点来进行松弛操作,直至队列空为止
期望的时间复杂度O(ke), 其中k为所有顶点进队的平均次数,可以证明k一般小于等于2。
实现方法:
1.存入图。可以使用链式前向星或者vector。
2.开一个队列,先将开始的节点放入。
3.每次从队列中取出一个节点X,遍历与X相通的Y节点,查询比对 Y的长度 和 X的长度+ X与Y的长度
如果X的长度+ X与Y的长度 > Y的长度,说明需要更新操作。
1).存入最短路。
2).由于改变了原有的长度,所以需要往后更新,与这个节点相连的最短路。(即:判断下是否在队列,在就不用重复,不在就加入队列,等待更新)。
3).在这期间可以记录这个节点的进队次数,判断是否存在负环。
4.直到队空。
判断有无负环:如果某个点进入队列的次数超过N次则存在负环
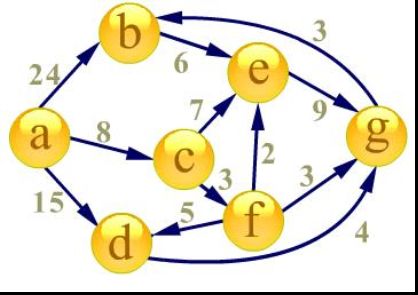
模拟过程:
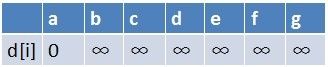
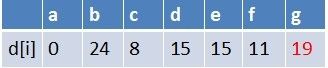
首先建立起始点a到其余各点的最短路径表格
首先源点a入队,当队列非空时:
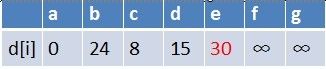
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要入队,此时队列中的元素为c,d,e
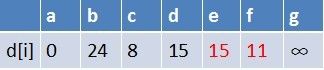
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此e不用入队了,f要入队,此时队列中的元素为d,e,f
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
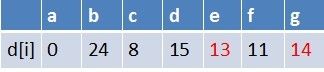
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:
在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
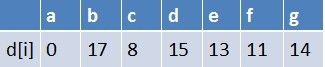
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
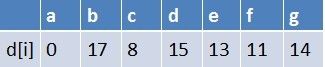
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:
在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为14
SPFA核心代码:
bool SPFA(int s,int n)
{
queue q;
memset(vis,inf,sizeof(vis));
memset(ven,0,sizeof(ven));
memset(nums,0,sizeof(nums));
vis[s]=0;//初始化距离
ven[s]=1,nums[s]++;//标记s节点在队列,队列次数+1
q.push(s);
while(!q.empty())
{
int x=q.front();
q.pop();//出队
ven[x]=0;//标记不在队列
for(int i=pre[x]; ~i; i=a[i].next)//遍历与x节点连通的点
{
int y=a[i].y;
if(vis[y]>vis[x]+a[i].time)//更新
{
vis[y]=vis[x]+a[i].time;
if(!ven[y])
//由于更新了节点,所以后续以这个为基础的最短路,也要更新下
//所以如果在队列就不用加入,不在的话加入更新后续节点
{
q.push(y);
ven[y]=1;//标记这个节点在队列中
nums[y]++;//记录加入次数
if(nums[y]>n)//如果这个点加入超过n次,说明存在负圈,直接返回
return false;
}
}
}
}
return true;
} 扔个例题~(hdu 2066)
虽然草儿是个路痴(就是在杭电待了一年多,居然还会在校园里迷路的人,汗~),但是草儿仍然很喜欢旅行,因为在旅途中 会遇见很多人(白马王子,^0^),很多事,还能丰富自己的阅历,还可以看美丽的风景……草儿想去很多地方,她想要去东京铁塔看夜景,去威尼斯看电影,去阳明山上看海芋,去纽约纯粹看雪景,去巴黎喝咖啡写信,去北京探望孟姜女……眼看寒假就快到了,这么一大段时间,可不能浪费啊,一定要给自己好好的放个假,可是也不能荒废了训练啊,所以草儿决定在要在最短的时间去一个自己想去的地方!因为草儿的家在一个小镇上,没有火车经过,所以她只能去邻近的城市坐火车(好可怜啊~)。
Input
输入数据有多组,每组的第一行是三个整数T,S和D,表示有T条路,和草儿家相邻的城市的有S个,草儿想去的地方有D个;
接着有T行,每行有三个整数a,b,time,表示a,b城市之间的车程是time小时;(1=<(a,b)<=1000;a,b 之间可能有多条路)
接着的第T+1行有S个数,表示和草儿家相连的城市;
接着的第T+2行有D个数,表示草儿想去地方。
Output
输出草儿能去某个喜欢的城市的最短时间。
Sample Input
6 2 3
1 3 5
1 4 7
2 8 12
3 8 4
4 9 12
9 10 2
1 2
8 9 10
Sample Output
9
#include
#define inf 0x3f3f3f3f
using namespace std;
const int M=10005;
struct A {
int y,time,next;
} a[M<<1];
int pre[M],cent=0;//链式前向星数组
int vis[M],ven[M],nums[M]; //SPFS数组,vis记录最短路,ven记录是否在队列,nums记录入队次数
void add(int x,int y,int k) { //链式前向星,加入节点
a[cent].y=y, a[cent].time=k, a[cent].next=pre[x];
pre[x]=cent++;
}
bool SPFA(int s,int n) {
queue q;
memset(vis,inf,sizeof(vis));
memset(ven,0,sizeof(ven));
memset(nums,0,sizeof(nums));
vis[s]=0;//初始化距离
ven[s]=1,nums[s]++;//标记s节点在队列,队列次数+1
q.push(s);
while(!q.empty()) {
int x=q.front();
q.pop();//出队
ven[x]=0;//标记不在队列
for(int i=pre[x]; ~i; i=a[i].next) { //遍历与x节点连通的点
int y=a[i].y;
if(vis[y]>vis[x]+a[i].time) { //更新
vis[y]=vis[x]+a[i].time;
if(!ven[y]) { //所以如果在队列就不用加入,不在的话加入更新后续节点
q.push(y);
ven[y]=1;//标记这个节点在队列中
nums[y]++;//记录加入次数
if(nums[y]>n) return false;//如果这个点加入超过n次,说明存在负圈,直接返回
}
}
}
}
return true;
}
int main() {
int n,m,t;
int b[M],c[M];
while(cin>>n>>m>>t) {
cent=0;
memset(pre,-1,sizeof(pre));
for(int i=0; i>x>>y>>k;
add(x,y,k);
add(y,x,k);
}
for(int i=0; i>b[i];
for(int i=0; i>c[i];
int minn=inf;
for(int i=0; i
由A*引发的连环惨案(SPFA、dijkstra、链式前向星)我哭了
近一年后,我果然忘得一干二净,然后重温了一遍,又做了个题,记录一下:
数据比较水,因为基本都在卡spfa,只是想多掌握一种思想
洛谷 P3371 【模板】单源最短路径(弱化版)
题目背景
本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式
第一行包含三个整数 n,m,sn,m,sn,m,s,分别表示点的个数、有向边的个数、出发点的编号。
接下来 mmm 行每行包含三个整数 u,v,wu,v,wu,v,w,表示一条 u→vu \to vu→v 的,长度为 www 的边。
输出格式
输出一行 nnn 个整数,第 iii 个表示 sss 到第 iii 个点的最短路径,若不能到达则输出 231−12^{31}-1231−1。
输入输出样例
输入
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出
0 2 4 3
代码:
#include
const long long inf=2147483647;
const int maxn=10005;
const int maxm=500005;
using namespace std;
int n,m,s,num_edge=0;
int dis[maxn],vis[maxn],head[maxm];
struct Edge
{
int next,to,dis;
}edge[maxm]; //结构体表示静态邻接表
void addedge(int from,int to,int dis) //邻接表建图
{ //以下是数据结构书上的标准代码,不懂翻书看解释
edge[++num_edge].next=head[from]; //链式存储下一条出边
edge[num_edge].to=to; //当前节点编号
edge[num_edge].dis=dis; //本条边的距离
head[from]=num_edge; //记录下一次的出边情况
}
void spfa()
{
queue q; //spfa用队列,这里用了STL的标准队列
for(int i=1; i<=n; i++)
{
dis[i]=inf; //带权图初始化
vis[i]=0; //记录点i是否在队列中,同dijkstra算法中的visited数组
}
q.push(s); dis[s]=0; vis[s]=1; //第一个顶点入队,进行标记
while(!q.empty())
{
int u=q.front(); //取出队首
q.pop(); vis[u]=0; //出队标记
for(int i=head[u]; i; i=edge[i].next) //邻接表遍历,不多解释了(也可用vector代替)
{
int v=edge[i].to;
if(dis[v]>dis[u]+edge[i].dis) //如果有最短路就更改
{
dis[v]=dis[u]+edge[i].dis;
if(vis[v]==0) //未入队则入队
{
vis[v]=1; //标记入队
q.push(v);
}
}
}
}
}
int main()
{
cin>>n>>m>>s;
for(int i=1; i<=m; i++)
{
int f,g,w;
cin>>f>>g>>w;
addedge(f,g,w); //建图,有向图连一次边就可以了
}
spfa(); //开始跑spfa
for(int i=1; i<=n; i++)
if(s==i) cout<<0<<" "; //如果是回到自己,直接输出0
else cout<