C++数据结构——数组与广义表
C++数据结构——数组与广义表
参考博客：
（1）理论：https://www.cnblogs.com/KennyRom/p/5971853.html
（2）理论：https://www.cnblogs.com/zyrblog/p/6870097.html
（3）题型：https://www.cnblogs.com/xingyunblog/p/4229812.html
（4）数据结构小结（五）数组与广义表
一、数组
1、数组的定义、特点、操作
（1） 数组的定义：
1）一个 N 维数组是受 N 组线性关系约束的线性表。详细定义见数组定义。
2）一维数组是定长线性表； 二维数组是一个定长线性表，它的每个元素是一个一维数组；n维数组是线性表，它的每个元素是n-1维数组。
（2） 数组的特点：元素数目固定且下标有界。
（3） 数组的操作：按照下标进行读写。
2、数组的顺序表示与实现
由于数组一般不作插入与删除操作，一旦建立了数组，结构中的数据元素个数和元素之间的关系就不再发生变动，因此，采用顺序存储结构表示数组是自然的事。计算机的内存结构是一维的，因此用一维内存来表示多维数组，就必须按某种次序将数组元素排成一列序列，然后将这个线性序列存放在储存器中。
通常有两种顺序存储方式：
（1）行优先顺序——将数组元素按行排列
在PASCAL、C语言中，数组就是按行优先顺序储存。（C/C++，Python，Java）
（2）列优先顺序——将数组按列向量排列。
在FORTRAN语言中，数组就是按列优先顺序储存的。（FORTRAN，Matlab）
3、矩阵的压缩存储
（1）定义
为节省储存空间，矩阵进行压缩存储：即为多个相同的非零的元素值分配一个储存空间；对0元素不分配空间。
（2）特殊矩阵
对称矩阵，三角矩阵等特殊矩阵的存储方法：非零元素的分布都有一个明显的规律，从而都可将其压缩存储到一维数组中，并找到每个非零元在一维数组中的对应关系。
（3）稀疏矩阵
1）定义
假设在mxn的矩阵中，有t个元素不为0，令delta=t/(mxn)，称delta为矩阵的稀疏因子，通常认为delta <= 0.05 时将矩阵称为稀疏矩阵。
2）如何进行稀疏矩阵的压缩存取呢？
A、三元组顺序表（参考博客：https://www.cnblogs.com/KennyRom/p/5971853.html）
用三项内容表示稀疏矩阵中的每个非零元素，进行形式为：（i,j,value），其中i表示行序号，j表示列序 号，value表示非零元素的值。
//稀疏矩阵，非零元素比较少
const int max=1000;
template
typedef struct
{
int i, j;
Object e;
}Triple;
template
typedef struct
{
Triple 稀疏矩阵的转置算法：转置前矩阵为M，转置后为T，M的列为T的行，因此，要按M.data的列序转置所得到的转置矩阵T的三元组表必定按行优先存放。其转置算法时间复杂度为O(n*t)，代码为：
template
void trans( TSMattrix 快速转置算法：
一遍扫描先确定三元组的位置关系，二次扫描由位置关系装入三元组。为了预先确定矩阵M中的每一列的第一个非零元素在数组B中应有的位置，需要闲球的矩阵M中的每一列中非零元素的个数。为此，需要设计两个一位数组num[0...n-1]和cpot[1..n-1]，num[0...n-1]：统计M中每一列非零元素的个数。cpot[0...n-1]：由递推关系得出M中的每列第一个非零元素在B中的位置，cpot[col]=cpot[col-1]+num[col-1]。算法时间复杂度为O(n+t)，代码如下：
template
void fasttranstri( TSMatrix B、行逻辑链接的顺序表
将快速转置矩阵的算法中创建的指示“行”信息的辅助数组cpot固定在稀疏矩阵的存储结构中，称这种“带行链接信息”的三元组表为行逻辑链接的顺序表。
C、十字链表
当矩阵的非零元个数和位置在操作过程中变化较大时，就不宜采用顺序存储结构来表示三元组的线性表了。
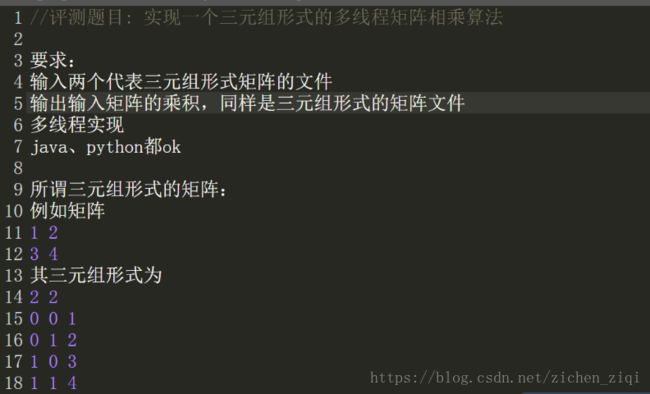
3)稀疏矩阵的运算操作（矩阵的乘法）——多线程稀疏矩阵乘法（python）
若用python进行稀疏矩阵的乘法操作，不调用from scipy import sparse，代码如下：
import numpy as np
import time
res = []
class SparseMultiply():
def __init__(self,ii,jj,A,B):
self.x, self.y = ii,jj
self.A, self.B = A, B
def run(self):
global res
A = self.A[self.A[:,0]==self.x]
B = self.B[self.B[:,1]==self.y]
value = 0.
for item1 in A:
for item2 in B:
if item1[1] == item2[0]:
value += item1[2]*item2[2]
res.append([self.x,self.y,value])
if "__main__" == __name__:
# 输入矩阵m1,m2
m1 = [[2,2],[0,0,1],[0,1,2],[1,0,3],[1,1,4]]
m2 = [[2,3],[0,0,2],[0,2,1],[1,2,3],[1,1,4]]
s1, s2 = m1[0], m2[0]
# 判断矩阵m1的列与m2的行数是否相等，若不等抛出异常
assert s1[1]==s2[0], '矩阵维度不匹配!'
m1_value = np.array(m1[1:])
m2_value = np.array(m2[1:])
rows, cols = s1[0], s2[1]
res.append([rows, cols])
# 调用类函数
for i in range(rows):
for j in range(cols):
SparseMultiply(i,j,m1_value,m2_value).run()
# 输出矩阵相乘结果
print (res)
运行结果：
[[2, 3], [0, 0, 2.0], [0, 1, 8.0], [0, 2, 7.0], [1, 0, 6.0], [1, 1, 16.0], [1, 2, 15.0]]a、参考博客：https://www.cnblogs.com/YiXiaoZhou/p/8810085.html
代码：
import threading, time
import numpy as np
res = []
class MyThread(threading.Thread):
def __init__(self,i,j,m1,m2):
threading.Thread.__init__(self)
self.x, self.y = i,j
self.m1, self.m2 = m1, m2
def run(self):
global res, lock
if lock.acquire():
m1 = self.m1[self.m1[:,0]==self.x]
m2 = self.m2[self.m2[:,1]==self.y]
value = 0.
for item1 in m1:
for item2 in m2:
if item1[1] == item2[0]:
value += item1[2]*item2[2]
res.append([self.x,self.y,value])
lock.release()
if "__main__" == __name__:
m1 = [[2,2],[0,0,1],[0,1,2],[1,0,3],[1,1,4]]
m2 = [[2,3],[0,0,2],[0,2,1],[1,2,3],[1,1,4]]
s1, s2 = m1[0], m2[0]
assert s1[1]==s2[0], 'mismatch'
m1_value = np.array(m1[1:])
m2_value = np.array(m2[1:])
rows, cols = s1[0], s2[1]
res.append([rows, cols])
ThreadList = []
lock = threading.Lock()
for i in range(rows):
for j in range(cols):
t = MyThread(i,j,m1_value,m2_value)
ThreadList.append(t)
for t in ThreadList:
t.start()
for t in ThreadList:
t.join()
print (res)运行结果：
[[2, 3], [0, 0, 2.0], [0, 1, 8.0], [0, 2, 7.0], [1, 0, 6.0], [1, 1, 16.0], [1, 2, 15.0]]参考计算：
b、三元稀疏矩阵的基本操作（参考博客：稀疏矩阵基本运算与稀疏矩阵的基本运算）
#include
#include
using namespace std;
int const N = 4; //常量 数组的大小
int const MaxSize = 100; // 最大 为100 常量
typedef int ElemType; // ElemType == int
typedef struct //结构体
{
int r; //行号
int c; //列号
ElemType d; //元素值
}TupNode; //三元组定义
typedef struct // 结构体
{
int rows; // 行
int cols; // 列
int nums; //非零元素个数
TupNode data[MaxSize];
}TsMatrix; //三元组存储结构
void CreatMat(TsMatrix &t, ElemType A[N][N]) //三元组表示稀疏矩阵
{
int i, j;
t.rows = N; t.cols = N; t.nums = 0; // 行列赋值
for (i = 0; ib.data[j].c)
{
c.data[k].r = b.data[j].r;
c.data[k].c = b.data[j].c;
c.data[k].d = b.data[j].d;
k++; j++;
}
else
{
v = a.data[i].d + b.data[j].d;
if (v != 0)
{
c.data[k].r = a.data[i].r;
c.data[k].c = a.data[i].c;
c.data[k].d = v;
k++;
}
i++; j++;
}
}
else if (a.data[i].r> insert;
switch (insert)
{
case 1:
{
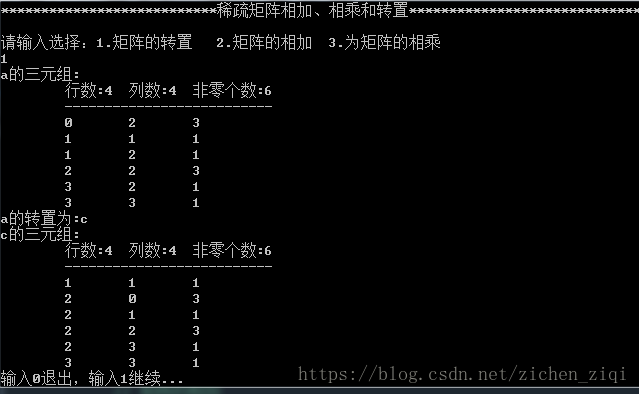
cout << "a的三元组:" << endl; // a的三元数组的输出
DispMat(a);
cout << "a的转置为:c" << endl; // a的转置为c
FastTranMat(a, c);
cout << "c的三元组:" << endl; DispMat(c); // c的三元矩阵的输出
break;
}
case 2:
{
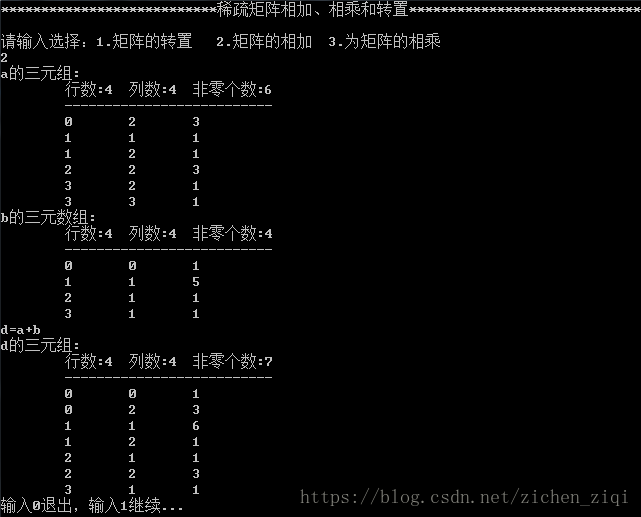
cout << "a的三元组:" << endl; // a的三元数组的输出
DispMat(a);
cout << "b的三元数组:" << endl; // b的三原数组的输出
DispMat(b);
cout << "d=a+b" << endl;
MatAdd(a, b, c);
cout << "d的三元组:" << endl; DispMat(c); // 矩阵的相加
break;
}
case 3:
{
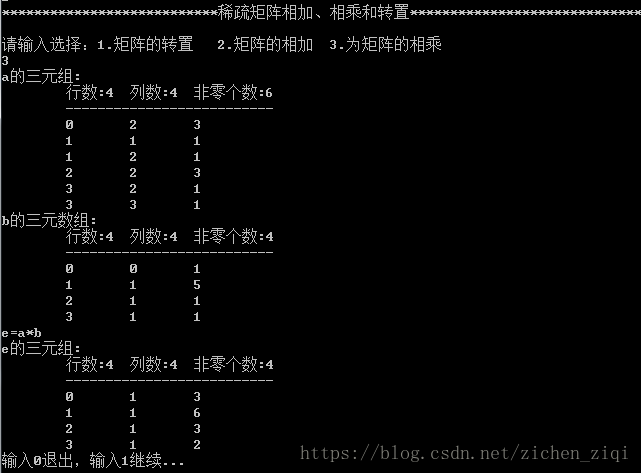
cout << "a的三元组:" << endl; // a的三元数组的输出
DispMat(a);
cout << "b的三元数组:" << endl; // b的三原数组的输出
DispMat(b);
cout << "e=a*b" << endl;
MatMul(a, b, c);
cout << "e的三元组:" << endl; DispMat(c); // 为矩阵的相乘
break;
}
default:{
cout << "输入错误" << endl;
}
}
cout << "输入0退出，输入1继续..." << endl;
cin >> flag;
}
}
运行结果：
二、广义表
