第三部分 数据结构 -- 第四章 图论算法1345：【例4-6】香甜的黄油

1345：【例4-6】香甜的黄油

时间限制: 1000 ms 内存限制: 65536 KB

【题目描述】
农夫John发现做出全威斯康辛州最甜的黄油的方法：糖。把糖放在一片牧场上，他知道N（1≤N≤500）只奶牛会过来舔它，这样就能做出能卖好价钱的超甜黄油。当然，他将付出额外的费用在奶牛上。

农夫John很狡猾。像以前的巴甫洛夫，他知道他可以训练这些奶牛，让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声，以至他可以在晚上挤奶。

农夫John知道每只奶牛都在各自喜欢的牧场（一个牧场不一定只有一头牛）。给出各头牛在的牧场和牧场间的路线，找出使所有牛到达的路程和最短的牧场（他将把糖放在那）。

【输入】
第一行: 三个数：奶牛数N，牧场数P（2≤P≤800），牧场间道路数C(1≤C≤1450)。

第二行到第N+1行: 1到N头奶牛所在的牧场号。

第N+2行到第N+C+1行：每行有三个数：相连的牧场A、B，两牧场间距（1≤D≤255），当然，连接是双向的。

【输出】
一行 输出奶牛必须行走的最小的距离和。

【输入样例】
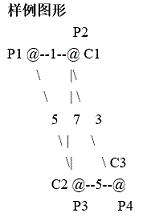
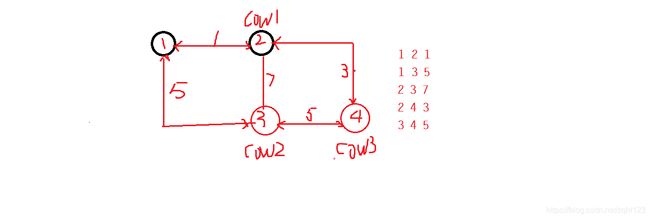
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
【输出样例】
8
【提示】
说明：放在4号牧场最优。

思路：求的是边权和最小的路径的最小和，主要算法为求最优路径的Dijstra或SPFA算法。依次枚举把糖放在第i个牧场，每枚举一个牧场计算出以i为牧场，到每个有奶牛的牧场的最短路径之和，取最小值，即为所求。注意：不是所有的牧场都有奶牛，在计算最短路径和时，是有奶牛的牧场的最短路径和。

#include
#include
#include
#include
#include
#define N 5005
using namespace std;
struct node{
	int w;
	int h;
}wh[5005]; 
int maxx,minn,f[N][N],dis[N];
int n, m ,x, y, t, k,g, mid, midd,a[N],h[N];
void spfa(int x)
{
	memset(dis,0x7f,sizeof(dis));
	bool b[N];
	dis[x] = 0;
	b[x] = 1;
	queue<int> q;
	q.push(x);
	while(!q.empty()){
		int top = q.front();
		q.pop();
		for(int  i = h[top];i;i = wh[i].h)
		{
			if(dis[wh[i].w] > dis[top] + f[top][wh[i].w])
			{
				dis[wh[i].w] = dis[top] + f[top][wh[i].w];
				if(!b[wh[i].w])
				{
					q.push(wh[i].w);
					b[wh[i].w] = 1;
				}
			}
		}
		b[top] = 0;
	}
}
int main(){
	maxx = mid = 1e9;
	scanf("%d%d%d",&n,&k,&m);
     for(int i = 1; i <= n; i++){
     	scanf("%d",&a[i]);
     	for(int j = 1; j <= n; j++)
     	f[i][j] = maxx;
     	f[i][i] = 0;
	 }
	  for(int i = 1; i <= m; i++)
	  {
	  	scanf("%d%d%d",&x,&y,&g);
	  	f[x][y] = f[y][x] = g;
	  	wh[++t] = (node){y,h[x]};h[x] = t;//邻接表 
	  	wh[++t] = (node){x,h[y]};h[y] = t;
		  
	  }
	  for(int i = 1; i <= k; i++)
	  {
	  	spfa(i);
	  	int ans = 0;
	  	for(int j = 1; j <= n; j++)
	  	ans += dis[a[j]];
	  	mid = min(mid,ans);
	  }
	 printf("%d",mid);
	return 0;
}