USACO 2019 OPEN TEST - Silver

1. Left Out

题目描述

Farmer John正在尝试给他的牛群拍照。根据以往的经验，他知道这一工作往往结果不怎么样。

这一次，Farmer John购买了一台昂贵的无人机，想要拍一张航拍照。为了使照片尽可能好看，他想让他的奶牛们在拍照时都朝向同一个方向。奶牛们现在在一块有围栏的草地上排列成 $N\times N$ 的方阵，例如：

RLR
RRL
LLR

这里，字符 R 表示一头朝右的奶牛，字符 L 表示一头朝左的奶牛。由于奶牛们都挤在一起，Farmer John没办法走到某一头奶牛面前让她调转方向。他能做的只有对着某一行或某一列的奶牛喊叫让她们调转方向，使得被叫到的这一行或列内的所有 L 变为 R，R 变为 L。Farmer John可以对任意多的行或列发号施令，也可以对同一行或列多次发令。

就如同Farmer John想象的，他发现他不可能让他的奶牛们都朝向同一个方向。他最多能做的是让所有奶牛中除了一头之外都朝向相同的方向。请找出这样的一头奶牛。

输入格式

输入的第一行包含 $N$ 。以下 $N$ 行描述了奶牛方阵的第 $1\dots N$ 行，每行包含一个长度为 $N$ 的字符串。

输出格式

输出一头奶牛的行列坐标，满足这头奶牛被调转方向的话，Farmer John就可以使他的所有奶牛都朝向同一个方向。如果不存在这样的奶牛，输出 $-1$。如果存在多头这样的奶牛，输出其中行坐标最小的，如果多头这样的奶牛具有相同的行坐标，输出其中列坐标最小的。

样例输入

3
RLR
RRL
LLR

样例输出

1 1

数据范围与说明

在这个例子中，位于第 $1$ 行第 $1$ 列（左上角）的奶牛是那头令人讨厌的奶牛，因为Farmer John可以喊叫第2行和第3列来让所有奶牛都面向左侧，只有这一头奶牛面向右侧。

对于 $100\%$ 的数据，$2\le N\le 1000$。

T1 题解

作为USACO银组的第一道题，这题还是很考察思维水平的。像我用了一个半小时写了个 $40$ 分的 $DP$，却没想到这题是道结论题。

我们不妨可以设 $L$ 为 $0$，$R$ 为 $1$。那么题面翻译过来就是经过 $n$ 次行列变换之后（因为 $0$ 和 $1$ 是互相对立的），将这个矩阵变成只有一个 $1$ 或者只有一个 $0$。否则输出 $-1$。

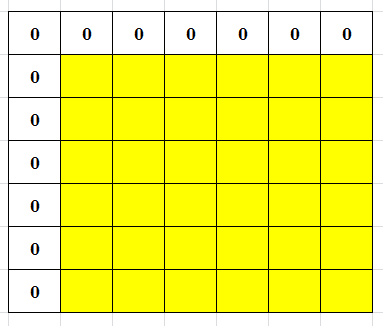
我们可以先考虑将矩阵的第一行和第一列全变成 $0$。也就是下图中的情况。具体做法就是：如果在第一行或者第一列上存在 $1$，那么就可以翻转这一行或者这一列。

然后，我们的答案就存在一下 $4$ 种情况：

1. 如果黄色部分都是 $1$ 的话，那么答案就是 1 1，因为我们可以翻转第一行与第一列，使得除 1 1 外所有的点都是 $1$。特别的，当 $n=2$ 时，是可以做到全为 $0$ 或全为 $1$，做法可以自己推

2. 如果黄色部分只有一个 $1$，其他部分都是 $0$ 时，答案显然就是这个点

3. 如果在黄色部分（$(n-1)\times (n-1)$ 的矩阵中），有一行全为 $1$，其他全为 $0$ 时，就如下图所示，那么答案就是这一行第一个元素。因为这行经过翻转就可以让这行第一列的元素为 $1$。同理，一列全为 $1$ 也就是这种情况。

   

4. 如果以上 $3$ 中情况均不满足，就是不存在答案。

T1代码

#include 
#define M 1010
using namespace std;

int n, m, s, ans=0;
int a[M][M]={0};
char c[M][M];

int main()
{
    memset(a,0,sizeof(a));
    scanf("%d",&n);
    if(n==1) {printf("-1\n"); return 0;}
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=n;++j)
        {
            cin>>c[i][j];
            if(c[i][j]=='L') a[i][j]=0;
            else a[i][j]=1;
        }
    }
    for(int i=1;i<=n;++i)
    {
        if(a[i][1]!=0)
        {
            for(int j=1;j<=n;++j) a[i][j]^=1;
        }
    }
    for(int j=2;j<=n;++j)
    {
        if(a[1][j]!=0)
        {
            for(int i=1;i<=n;++i) a[i][j]^=1;
        }
    }
    int cnt=0;
    for(int i=2;i<=n;++i) for(int j=2;j<=n;++j) cnt+=a[i][j];
    if(cnt==(n-1)*(n-1))
    {
        if(n==2) printf("-1\n"); else printf("1 1\n");
    }
    else if(cnt==1)
    {
        for(int i=2;i<=n;++i) for(int j=2;j<=n;++j) if(a[i][j]) printf("%d %d\n",i,j);
    }
    else if(cnt==n-1)
    {
        for(int i=1;i<=n;++i)
        {
            int sum=0;
            for(int j=1;j<=n;++j) sum+=a[i][j];
            if(sum==n-1)
            {
                printf("%d 1\n",i);
                return 0;
            }
        }
        for(int j=1;j<=n;++j)
        {
            int sum=0;
            for(int i=1;i<=n;++i) sum+=a[i][j];
            if(sum==n-1)
            {
                printf("1 %d\n",j);
                return 0;
            }
        }
    }
    else printf("-1\n");
    return 0;
}

2. Cow Steeplechase II

题目描述

在过去，Farmer John曾经构思了许多新式奶牛运动项目的点子，其中就包括奶牛障碍赛，是奶牛们在赛道上跑越障碍栏架的竞速项目。他之前对推广这项运动做出的努力结果喜忧参半，所以他希望在他的农场上建造一个更大的奶牛障碍赛的场地，试着让这项运动更加普及。

Farmer John为新场地精心设计了 $N$ 个障碍栏架，编号为 $1\dots N$，每一个栏架都可以用这一场地的二维地图中的一条线段来表示。这些线段本应两两不相交，包括端点位置。

不幸的是，Farmer John在绘制场地地图的时候不够仔细，现在发现线段之间出现了交点。然而，他同时注意到只要移除一条线段，这张地图就可以恢复到预期没有相交线段的状态（包括端点位置）。

请求出Farmer John为了恢复没有线段相交这一属性所需要从他的计划中删去的一条线段。如果有多条线段移除后均可满足条件，请输出在输入中出现最早的线段的序号。

输入格式

输入的第一行包含 $N$ 。余下 $N$ 行每行用四个整数 $x_1,y_1,x_2,y_2$ 表示一条线段，表示这条线段的端点为 $(x_1,y_1)$ 和 $(x_2,y_2)$ 。所有线段的端点各不相同。

输出格式

输出在输入中出现最早的移除之后可以使得余下线段各不相交的线段序号。

样例输入

4
2 1 6 1
4 0 1 5
5 6 5 5
2 7 1 3

样例输出

2

数据范围与提示

由于线段端点坐标数值的大小，在这个问题中你可能需要考虑整数类型溢出的情况。

对于 $30\%$ 的数据，$2\le N\le 1000$。

对于 $100\%$ 的数据，$2\le N\le 10^5$，$1\le x_1,x_2,y_1,y_2\le 10^9$。

T2题解与代码

因为这题十分毒瘤，一下的分析均选自peter9the6ghost的博客。

这题正解当然是 $set$+扫描线，没什么好说的，但是我最开始做这道题的时候觉得就一个silver，怎么可能这么毒，于是开始用noipcsp的思维乱 $yy$，结果想出来了一个理论 $n^2$ 但是实际上及其优秀的算法。

首先，绝对 $n^2$ 的算法应该不难对吧：

这里我们考虑进行优化。可以看出来对于每一条线段，与其相交的线段都是有一定关联的，那么我们就将这样关联的线段集中在一起。

对于一条线段，左右端点交换不会对其产生影响，所以我们进行调整：我们维护这样一个关系：$y_1\le y_2$ 当 $y_1=y_2$ 的时候，维护 $x_1<x_2$。

再对于所有线段，我们以 $y_1$ 为第一关键字，$x_1$ 为第二关键字排序。

这里我们可以轻易的发现:对于任何一条线段 $Se{g}_i$，只有可能与 $Se{g}_j$ 相交，（这里 $Se{g}_j$ 保证 $Se{g}_j\text{->}y1\le Se{g}_i\text{->}y2$）。这就是一个连续的区间了（虽然还是理论 $O(n^2)$ 但是实际上飞快）！

接下来就剩线段相交基本操作了。

线段相交： 这里我并没有使用计算几何,而是非常单纯而noip暴力地用平面几何芝士进行判定

tips:这里需要特别注意线段竖直与两线段交点的判定

db Gety(Segment a,db x){
    //计算直线a在x的y值
    db k=(a.y2-a.y1)/(a.x2-a.x1),b=a.y1-k*a.x1;
    return k*x+b;
}
db CrossPointx(Segment a,Segment b){
    if(a.x1>a.x2)swap(a.x1,a.x2),swap(a.y1,a.y2);
    if(b.x1>b.x2)swap(b.x1,b.x2),swap(b.y1,b.y2);
    db k1=(a.y2-a.y1)/(a.x2-a.x1);db b1=a.y1-k1*a.x1;
    db k2=(b.y2-b.y1)/(b.x2-b.x1);db b2=b.y1-k2*b.x1;
    //平行return -1是因为原题中所有坐标维护在x正半轴,y正半轴和第二象限内
    if(k1==k2)return -1;
    return (b2-b1)/(k1-k2);
}
bool Cross(ll aa,ll bb){
    Segment a=seg[aa],b=seg[bb];db tmp;
    //两条线段都竖直
    if(a.x1==a.x2&&b.x1==b.x2)return a.y1<b.y2&&a.y2>=b.y1&&a.x1==b.x1;
    //第一条竖直
    if(a.x1==a.x2){
        tmp=Gety(b,a.x1);
        return tmp>=a.y1&&tmp<=a.y2&&tmp>=b.y1&&tmp<=b.y2;
    }
    //第二条竖直
    if(b.x1==b.x2){
        tmp=Gety(a,b.x1);
        return tmp>=a.y1&&tmp<=a.y2&&tmp>=b.y1&&tmp<=b.y2;
    }
    //两条都不特殊
    tmp=CrossPointx(a,b);//交点x坐标
    return tmp>=Min(a.x1,a.x2)&&tmp<=Max(a.x1,a.x2)&&tmp>=Min(b.x1,b.x2)&&tmp<=Max(b.x1,b.x2);
}

算法本体介绍：

首先按上述方式给线段排序，然后找出相交的任意两条线段（记为 $x,y$），分别求出与这两条线段相交的线段条数，记为 $nu{m}_x,nu{m}_y$。

这里可以发现如果两个 $num$ 不同,则答案必定是 $num$ 大的那一条线段,证明如下：

这里使用反证法，假设我们要选择的是 $num$ 小的那条线段 $y$，那么与 $x$ 相交的 $nu{m}_x$ 条线段中必然有一些线段仍然与 $x$ 相交，所以不能选 $y$！

如果 $num$ 相同的话就输出编号小的咯。

代码就在下面：

#include
#define ll long long
#define db double
#define maxn 100005
#define Max(a,b) (((a)>(b))?(a):(b))
#define Min(a,b) (((a)<(b))?(a):(b))
using namespace std;
ll read(){
    ll a=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){a=a*10+c-'0';c=getchar();}
    return a*f;
}
struct Segment{db x1,y1,x2,y2,id;}seg[maxn];
int cmp(Segment a,Segment b){
    if(a.y1!=b.y1)return a.y1<b.y1;
    return a.x1<b.x1;
}
db Gety(Segment a,db x){
    db k=(a.y2-a.y1)/(a.x2-a.x1),b=a.y1-k*a.x1;
    return k*x+b;
}
db CrossPointx(Segment a,Segment b){
    if(a.x1>a.x2)swap(a.x1,a.x2),swap(a.y1,a.y2);
    if(b.x1>b.x2)swap(b.x1,b.x2),swap(b.y1,b.y2);
    db k1=(a.y2-a.y1)/(a.x2-a.x1);db b1=a.y1-k1*a.x1;
    db k2=(b.y2-b.y1)/(b.x2-b.x1);db b2=b.y1-k2*b.x1;
    if(k1==k2)return -1;
    return (b2-b1)/(k1-k2);
}
bool Cross(ll aa,ll bb){
    Segment a=seg[aa],b=seg[bb];db tmp;
    if(a.x1==a.x2&&b.x1==b.x2)return a.y1<b.y2&&a.y2>=b.y1&&a.x1==b.x1;
    if(a.x1==a.x2){tmp=Gety(b,a.x1);return tmp>=a.y1&&tmp<=a.y2&&tmp>=b.y1&&tmp<=b.y2;}
    if(b.x1==b.x2){tmp=Gety(a,b.x1);return tmp>=a.y1&&tmp<=a.y2&&tmp>=b.y1&&tmp<=b.y2;}
    tmp=CrossPointx(a,b);
    return tmp>=Min(a.x1,a.x2)&&tmp<=Max(a.x1,a.x2)&&tmp>=Min(b.x1,b.x2)&&tmp<=Max(b.x1,b.x2);
}
ll n;
ll Check(ll x){
    ll ret=0;
    for(int i=1;i<=n;i++){
        if(i==x)continue;
        ret+=Cross(Min(i,x),Max(i,x));
    }
    return ret;
}
int main(){
    n=read();
    for(int i=1,x1,x2,y1,y2;i<=n;i++){
        x1=read();y1=read();
        x2=read();y2=read();
        if(y1>y2){swap(x1,x2);swap(y1,y2);}
        if(y1==y2&&x1>x2){swap(x1,x2);}
        seg[i]=(Segment){x1,y1,x2,y2,i};
    }
    sort(seg+1,seg+n+1,cmp);
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            if(seg[j].y1>seg[i].y2)break;
            if(Cross(i,j)){
                ll num1=Check(i),num2=Check(j);
                if(num1==num2)cout<<Min(seg[i].id,seg[j].id);
                else cout<<(num1>num2?seg[i].id:seg[j].id);
                return 0;
            }
        }
    }
    return 0;
}
/*
5
7 1 4 0
2 1 2 6
1 4 4 2
3 2 4 3
5 2 5 5
*/
/*
9
9 6 6 8
8 5 6 5
8 4 4 1
4 9 4 5
8 3 7 0
0 7 1 2
7 4 9 5
6 9 6 4
2 1 7 7
*/
//这是作者自己hack的数据

3. Fence Planning

题目描述

Farmer John的 $N$ 头奶牛，编号为 $1\dots N$，拥有一种围绕“哞网”，一些仅在组内互相交流却不与其他组进行交流的奶牛小组，组成的复杂的社交网络。

每头奶牛位于农场的二维地图上的不同位置 $(x,y)$，并且我们知道有 $M$ 对奶牛会相互哞叫。两头相互哞叫的奶牛属于同一哞网。

为了升级他的农场，Farmer John想要建造一个四边形与 $x$ 轴和 $y$ 轴平行的长方形围栏。Farmer John想要使得至少一个哞网完全被围栏所包围（在长方形边界上的奶牛计为被包围的）。请帮助Farmer John求出满足他的要求的围栏的最小可能周长。

输入格式

输入的第一行包含 $N$ 和 $M$。以下 $N$行每行包含一头奶牛的 $x$ 坐标和 $y$ 坐标。以下 $M$ 行每行包含两个整数 $a$ 和 $b$，表示奶牛 $a$ 和 $b$ 之间有哞叫关系。每头奶牛都至少存在一个哞叫关系，并且输入中不会出现重复的哞叫关系。

输出格式

输出满足Farmer John的要求的围栏的最小周长。

样例输入

7 5
0 5
10 5
5 0
5 10
6 7
8 6
8 4
1 2
2 3
3 4
5 6
7 6

样例输出

10

数据范围与提示

注意，题目中有可能出现围栏宽为 $0$ 或高为 $0$ 的情况。

对于 $30\%$ 的数据，$2\le N\le 1000$；

对于 $100\%$ 的数据，$2\le N\le 100000$，$1\le M\le 100000$，$0\le x,y\le 10^8$。

T3题解

这可能是这套题中最简单的一道题目。我们只需找出图中有多少个连通块，然后一个一个去更新最大值就可以了。

T3代码

#include 
#define Inf 0x3f3f3f3f
#define M 505000
using namespace std;

int n, m, ans=0, now=0;
int head[M], nex[M], to[M], tot=0;
struct Node{
	int dx, dy;
}a[M];
int vis[M];
vector<int> V[M];

inline int read()
{
	int re=0, f=1; char ch=getchar();
	while(ch<'0' || ch>'9') {if(ch=='-') f=-1; ch=getchar();}
	while(ch>='0' && ch<='9') {re=re*10+(ch-'0'); ch=getchar();}
	return re*f;
}

inline void add_edge(int x,int y)
{
	to[++tot]=y;
	nex[tot]=head[x];
	head[x]=tot;
}

inline void dfs(int x,int col)
{
	V[col].push_back(x);
	vis[x]=1;
	for(int i=head[x];i;i=nex[i])
	{
		if(vis[to[i]]) continue;
		dfs(to[i],col);
	}
}

int main()
{
	n=read(), m=read();
	for(int i=1;i<=n;++i) a[i].dx=read(), a[i].dy=read();
	for(int i=1;i<=m;++i)
	{
		int x=read(), y=read();
		add_edge(x,y);
		add_edge(y,x);
	}
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;++i) 
	{
		if(!vis[i])
		{
			now++;
			dfs(i,now);
		}
	}
	int Maxh=-Inf, Minh=Inf, Maxw=-Inf, Minw=Inf;
	ans=Inf;
	for(int i=1;i<=now;++i)
	{
		Maxh=-Inf, Minh=Inf, Maxw=-Inf, Minw=Inf;
		for(int j=0;j<V[i].size();++j)
		{
			Maxw=max(Maxw,a[V[i][j]].dx);
			Minw=min(Minw,a[V[i][j]].dx);
			Maxh=max(Maxh,a[V[i][j]].dy);
			Minh=min(Minh,a[V[i][j]].dy);
		}
		ans=min(ans,2*(Maxh-Minh+Maxw-Minw));
	}
	printf("%d\n",ans);
	return 0;
}