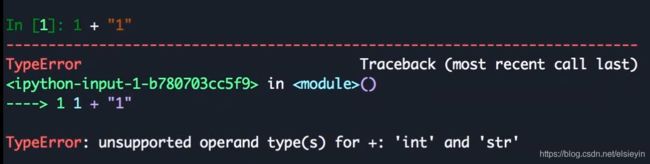
变量、运算符、数据类型
变量、运算符、数据类型
- Python语言特性
- Python2 3 区别
- 1 变量 可变类型 不可变类型
- 变量的内存地址 和值;
- `id()` 输出变量对应的内存地址
- 变量的基本类型 和声明
- 变量的类型转换
- 变量的命名规则
- 变量的多对多赋值,多变量返回
- input
- 2.1 注释
- 2.2 运算符
- 三元运算符:
- 运算
- 运算顺序
- 字符串拼接
- 变量
- 2.4 数据类型与转换
- bool(X)
- type() <> isinstance()
- 2.5 print() 函数
- 占位符
- 3.1 原码、反码和补码
- 3.2 按位非操作 ~
- 3.3 位运算
- 3.3 按位与操作 &
- 3.4 按位或操作 |
- 3.5 按位异或操作 ^
- 3.6 按位左移操作 <<
- 3.7 按位右移操作 >>
- 3.8 利用位运算实现快速计算
- 3.9 利用位运算实现整数集合
- 习题
- 位运算题解
- Refer:
Python语言特性
Python2 3 区别

左:py2 | 右: py3
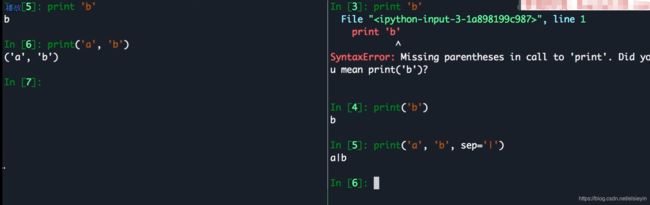
左边打印的是tuple,右 py3中,print 是函数 见2.5
1 变量 可变类型 不可变类型

定义变量不用数据类型声明,且确定一个变量的类型是第一次给他赋值的时候。
变量的内存地址 和值;
id() 输出变量对应的内存地址
python中会为每个对象分配内存,哪怕他们的值完全相等。id(object)函数是返回对象object在其生命周期内位于内存中的地址,id函数的参数类型是一个对象
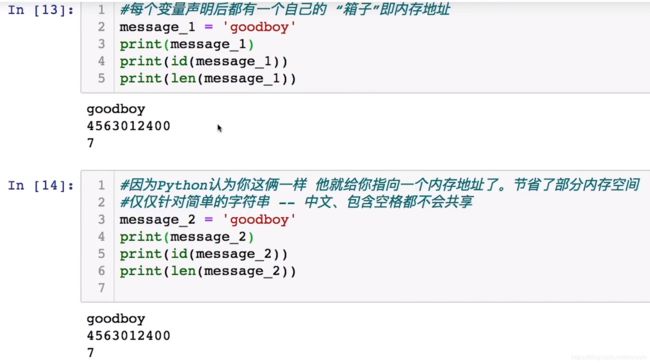
注意区分:带空格不会,中文不会
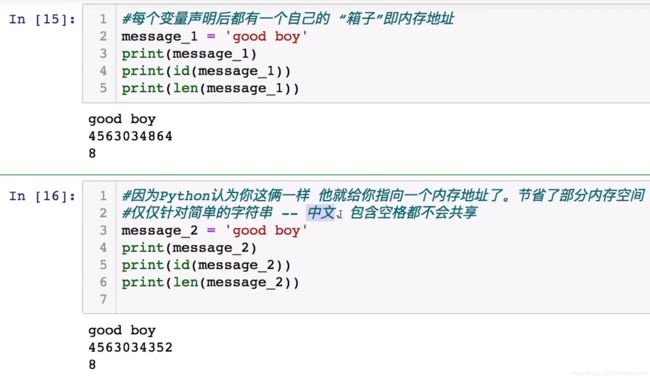

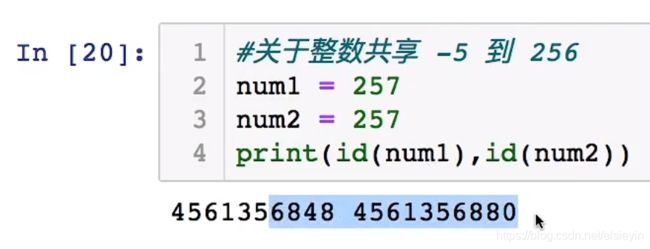



变量的基本类型 和声明
变量的类型转换

? 不可变类型 is, is not 和 ==,!= 等价
可变类型 两者有区别。

变量的命名规则

推荐使用『匈牙利命名法』,这也是在工作中最为规范的变量命名方式,有些时候看一个人写的代码,只需要看他写的变量名就能粗略判断出他的水平了。
简而言之,匈牙利命名法就是把变量的『类型』缩写,放到变量名的最前面。关键在于,这里说的变量『类型』,指的是那些和你的代码业务逻辑相关的类型。比如,在你的代码中有两个变量:students 和 teachers,他们分别代表的是用来存储学生的集合与用来存储老师的列表,使用『匈牙利命名法』后,可以把这两个名字改写成这样:
students -> set_students
teachers -> list_teachers
很多情况下,使用『匈牙利命名法』是个不错的主意,因为它可以改善你的代码可读性,尤其在那些变量众多、同一类型多次出现时,注意不要滥用就好
变量的多对多赋值,多变量返回
input
需要注意的是:当需要输入一个数字的时候,考虑到我们会用这个数字做计算,而Python3的input会默认转成str,所有我们需要把用户输入的数据转化成int
age = input('请输入年龄')
age = int(age) # 把字符串age转化成int类型age用于计算
2.1 注释
# 单行注释
“”"
多行
注释
“”"
2.2 运算符
三元运算符:
do sth1 if condition else do sth2
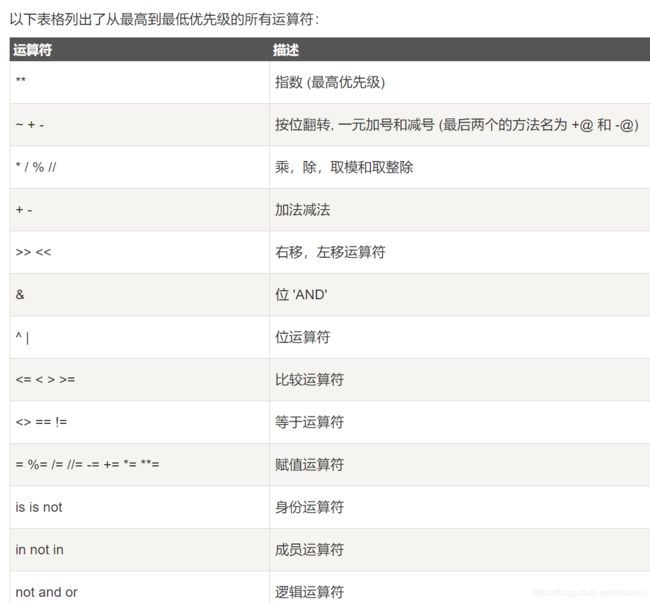
运算
运算顺序
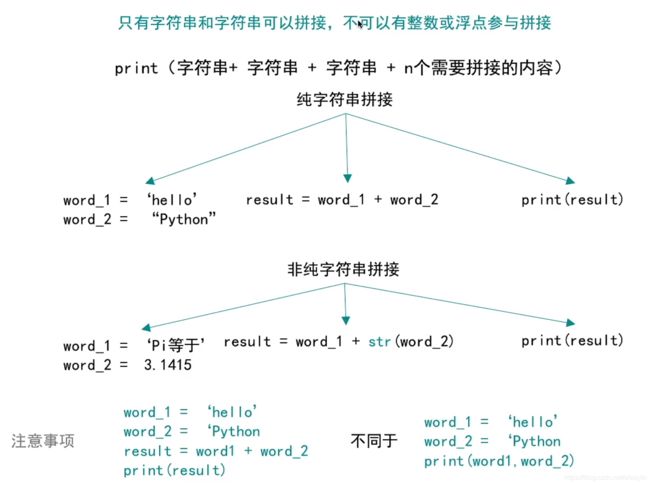
字符串拼接
变量
变量需先赋值,再使用?
变量名不能以数字开头。
变量名大小写敏感。
2.4 数据类型与转换
type()
dir() 查看其属性与方法
?什么叫bit_length
bool(X)
X 基本类型(除了0,0.0) 都是True
X 容器类型 只要非空,都是True
type() <> isinstance()
?什么叫:
- type()不会认为子类是一种父类类型,不考虑继承关系。
- isinstance()会认为子类是一种父类类型,考虑继承关系。
啥是父类类型? 啥是继承?
2.5 print() 函数
print(*objects, sep=' ', end='\n', file=sys.stdout, flush=False)
- 将对象以字符串表示的方式格式化输出到流文件对象file里。其中所有非关键字参数都按
str()方式进行转换为字符串输出; - 关键字参数
sep是实现分隔符,比如多个参数输出时想要输出中间的分隔字符; - 关键字参数
end是输出结束时的字符,默认是换行符\n; - 关键字参数
file是定义流输出的文件,可以是标准的系统输出sys.stdout,也可以重定义为别的文件; - 关键字参数
flush是立即把内容输出到流文件,不作缓存。
【例子】没有参数时,每次输出后都会换行。
shoplist = ['apple', 'mango', 'carrot', 'banana']
print("This is printed without 'end'and 'sep'.")
for item in shoplist:
print(item)
# This is printed without 'end'and 'sep'.
# apple
# mango
# carrot
# banana
【例子】每次输出结束都用end设置的参数&结尾,并没有默认换行。
shoplist = ['apple', 'mango', 'carrot', 'banana']
print("This is printed with 'end='&''.")
for item in shoplist:
print(item, end='&')
print('hello world')
# This is printed with 'end='&''.
# apple&mango&carrot&banana&hello world
【例子】item值与'another string'两个值之间用sep设置的参数&分割。由于end参数没有设置,因此默认是输出解释后换行,即end参数的默认值为\n。
shoplist = ['apple', 'mango', 'carrot', 'banana']
print("This is printed with 'sep='&''.")
for item in shoplist:
print(item, 'another string', sep='&')
# This is printed with 'sep='&''.
# apple&another string
# mango&another string
# carrot&another string
# banana&another string
占位符
其中第一个% 名字d那里是错的,但是%string可以接收28

3.1 原码、反码和补码
二进制有三种不同的表示形式:原码、反码和补码,计算机内部使用补码来表示。
原码:就是其二进制表示(注意,最高位是符号位)。
00 00 00 11 -> 3
10 00 00 11 -> -3
反码:正数的反码就是原码,负数的反码是符号位不变,其余位取反(对应正数按位取反)。
00 00 00 11 -> 3
11 11 11 00 -> -3
补码:正数的补码就是原码,负数的补码是反码+1。
00 00 00 11 -> 3
11 11 11 01 -> -3
符号位:最高位为符号位,0表示正数,1表示负数。在位运算中符号位也参与运算。
3.2 按位非操作 ~
3.3 位运算
正数 原码、 反码、 补码 相同
负数 原(符不变、其他取反=>) 反 (+1=>) 补
- 按位运算:
-
非
& 与
| 或
1就相当于True
a = 0011 1100
b = 0000 1101
-----------------
a&b = 0000 1100
a|b = 0011 1101
a^b = 0011 0001
~a = 1100 0011
不能直接写& 5
~x 等于x-1
~ 1 = 0
~ 0 = 1
~ 把num的补码中的 0 和 1 全部取反(0 变为 1,1 变为 0)有符号整数的符号位在 ~ 运算中同样会取反。
00 00 01 01 -> 5
~
---
11 11 10 10 -> -6
11 11 10 11 -> -5
~
---
00 00 01 00 -> 4
3.3 按位与操作 &
1 & 1 = 1
1 & 0 = 0
0 & 1 = 0
0 & 0 = 0
只有两个对应位都为 1 时才为 1
00 00 01 01 -> 5
&
00 00 01 10 -> 6
---
00 00 01 00 -> 4
3.4 按位或操作 |
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0
只要两个对应位中有一个 1 时就为 1
00 00 01 01 -> 5
|
00 00 01 10 -> 6
---
00 00 01 11 -> 7
3.5 按位异或操作 ^
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0
只有两个对应位不同时才为 1
00 00 01 01 -> 5
^
00 00 01 10 -> 6
---
00 00 00 11 -> 3
异或操作的性质:满足交换律和结合律
A: 00 00 11 00
B: 00 00 01 11
A^B: 00 00 10 11
B^A: 00 00 10 11
A^A: 00 00 00 00
A^0: 00 00 11 00
A^B^A: = A^A^B = B = 00 00 01 11
3.6 按位左移操作 <<
num << i 将num的二进制表示向左移动i位所得的值。
00 00 10 11 -> 11
11 << 3
---
01 01 10 00 -> 88
3.7 按位右移操作 >>
num >> i 将num的二进制表示向右移动i位所得的值。
00 00 10 11 -> 11
11 >> 2
---
00 00 00 10 -> 2
3.8 利用位运算实现快速计算
通过 <<,>> 快速计算2的倍数问题。
n << 1 -> 计算 n*2
n >> 1 -> 计算 n/2,负奇数的运算不可用
n << m -> 计算 n*(2^m),即乘以 2 的 m 次方
n >> m -> 计算 n/(2^m),即除以 2 的 m 次方
1 << n -> 2^n
通过 ^ 快速交换两个整数。
a ^= b
b ^= a
a ^= b
通过 a & (-a) 快速获取a的最后为 1 位置的整数。
00 00 01 01 -> 5
&
11 11 10 11 -> -5
---
00 00 00 01 -> 1
00 00 11 10 -> 14
&
11 11 00 10 -> -14
---
00 00 00 10 -> 2
3.9 利用位运算实现整数集合
?看不懂
一个数的二进制表示可以看作是一个集合(0 表示不在集合中,1 表示在集合中)。
比如集合 {1, 3, 4, 8},可以表示成 01 00 01 10 10 而对应的位运算也就可以看作是对集合进行的操作。
元素与集合的操作:
a | (1< 把 i 插入到集合中
a & ~(1< 把 i 从集合中删除
a & (1< 判断 i 是否属于该集合(零不属于,非零属于)
集合之间的操作:
a 补 -> ~a
a 交 b -> a & b
a 并 b -> a | b
a 差 b -> a & (~b)
注意:整数在内存中是以补码的形式存在的,输出自然也是按照补码输出。
【例子】C#语言输出负数。
class Program
{
static void Main(string[] args)
{
string s1 = Convert.ToString(-3, 2);
Console.WriteLine(s1);
// 11111111111111111111111111111101
string s2 = Convert.ToString(-3, 16);
Console.WriteLine(s2);
// fffffffd
}
}
【例子】 Python 的bin() 输出。
print(bin(3)) # 0b11
print(bin(-3)) # -0b11
print(bin(-3 & 0xffffffff))
# 0b11111111111111111111111111111101
print(bin(0xfffffffd))
# 0b11111111111111111111111111111101
print(0xfffffffd) # 4294967293
是不是很颠覆认知,我们从结果可以看出:
- Python中
bin一个负数(十进制表示),输出的是它的原码的二进制表示加上个负号,巨坑。 - Python中的整型是补码形式存储的。
- Python中整型是不限制长度的不会超范围溢出。
所以为了获得负数(十进制表示)的补码,需要手动将其和十六进制数0xffffffff进行按位与操作,再交给bin()进行输出,得到的才是负数的补码表示。
习题
leetcode 习题 136. 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
尝试使用位运算解决此题。
题目说明:
"""
Input file
example1: [2,2,1]
example2: [4,1,2,1,2]
Output file
result1: 1
result2: 4
"""
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# your code here
位运算题解
如果没有时间复杂度和空间复杂度的限制,这道题有很多种解法,可能的解法有如下几种。
使用集合存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。
使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。
使用集合存储数组中出现的所有数字,并计算数组中的元素之和。由于集合保证元素无重复,因此计算集合中的所有元素之和的两倍,即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次,其余元素都出现两次,因此用集合中的元素之和的两倍减去数组中的元素之和,剩下的数就是数组中只出现一次的数字。
上述三种解法都需要额外使用 O(n) 的空间,其中 nn 是数组长度。如果要求使用线性时间复杂度和常数空间复杂度,上述三种解法显然都不满足要求。那么,如何才能做到线性时间复杂度和常数空间复杂度呢?
答案是使用位运算。对于这道题,可使用异或运算 ⊕ \oplus ⊕。异或运算有以下三个性质。
任何数和 00 做异或运算,结果仍然是原来的数,即 a ⊕ 0 = a a \oplus 0=a a⊕0=a。
任何数和其自身做异或运算,结果是 0,即 a ⊕ a = 0 a \oplus a=0 a⊕a=0。
异或运算满足交换律和结合律,即 a ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ ( a ⊕ a ) = b ⊕ 0 = b a \oplus b \oplus a=b \oplus a \oplus a=b \oplus (a \oplus a)=b\oplus0=b a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

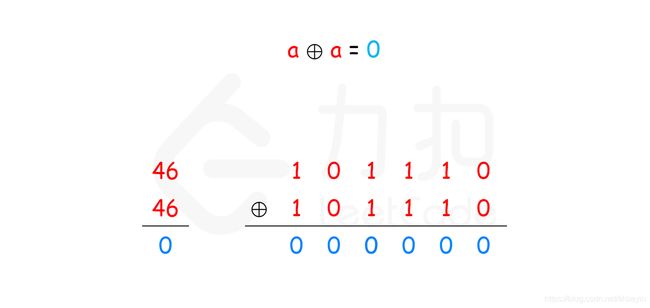

假设数组中有 2m+12m+1 个数,其中有 mm 个数各出现两次,一个数出现一次。令 a 1 a_{1} a1、 a 2 a_{2} a2 、 … \ldots …、 a m a_{m} am为出现两次的 mm 个数, a m + 1 a_{m+1} am+1为出现一次的数。根据性质 3,数组中的全部元素的异或运算结果总是可以写成如下形式:
( a 1 ⊕ a 1 ) ⊕ ( a 2 ⊕ a 2 ) ⊕ ⋯ ⊕ ( a m ⊕ a m ) ⊕ a m + 1 (a_{1} \oplus a_{1}) \oplus (a_{2} \oplus a_{2}) \oplus \cdots \oplus (a_{m} \oplus a_{m}) \oplus a_{m+1} (a1⊕a1)⊕(a2⊕a2)⊕⋯⊕(am⊕am)⊕am+1
根据性质 2 和性质 1,上式可化简和计算得到如下结果:
0 ⊕ 0 ⊕ ⋯ ⊕ 0 ⊕ a m + 1 = a m + 1 0 \oplus 0 \oplus \cdots \oplus 0 \oplus a_{m+1}=a_{m+1} 0⊕0⊕⋯⊕0⊕am+1=am+1
因此,数组中的全部元素的异或运算结果即为数组中只出现一次的数字。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
return reduce(lambda x, y: x ^ y, nums)
Refer:
- Datawhale Python
- 慕课网python后端面试课程
- 马一特-Python通用教程
- 万门python基础趣讲精练
- 力扣题解