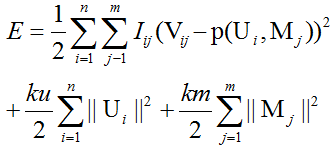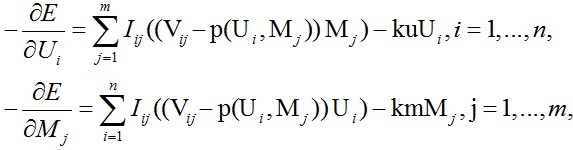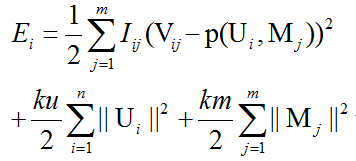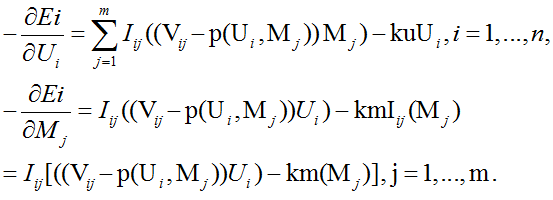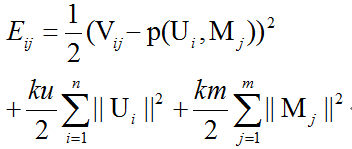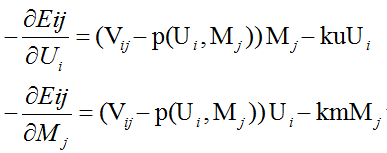基于矩阵分解的隐因子模型

推荐系统是现今广泛运用的一种数据分析方法。常见的如，“你关注的人也关注他”，“喜欢这个物品的用户还喜欢。。”“你也许会喜欢”等等。

常见的推荐系统分为基于内容的推荐与基于历史记录的推荐。

基于内容的推荐，关键在于提取到有用的用户，物品信息，以此为特征向量来进行分类，回归。

基于历史记录的推荐，记录用户的评分，点击，收藏等等行为，以此来判断。

基于内容的推荐对于用户物品的信息收集度要求比较高，而许多情况下很难得到那么多的有用信息。而基于历史记录的方法，则利用一些常见的历史记录，相比与基于内容的方法，数据的收集比较容易。

协同过滤广泛运用在推荐系统中。一般的方式是通过相似性度量，得到相似的用户集合，或者相似的物品集合，然后据此来进行推荐。

Amazon的图书推荐系统就是使用的基于物品相似性的推荐，“我猜你还喜欢**物品”。

不过，简单的协同过滤效果不是很好，我们或考虑用户聚类，得到基于用户的协同过滤；或只考虑物品聚类，得到基于物品的协同过滤。

有人提出了基于矩阵分解（SVD）的隐因子模型（Latent Factor Model）。

隐因子模型通过假设一个隐因子空间，分别得到用户，物品的类别矩阵，然后通过矩阵相乘得到最后的结果。在实践中，LFM的效果会高于一般的协同过滤算法。

 

1.      LFM基本方法

 

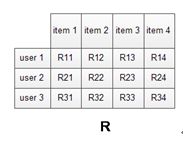
我们用user1,2,3表示用户，item 1,2,3表示物品，Rij表示用户i对于物品j的评分，也就是喜好度。那么我们需要得到一个关于用户-物品的二维矩阵，如下面的R。

常见的系统中，R是一个非常稀疏的矩阵，因为我们不可能得到所有用户对于所有物品的评分。于是利用稀疏的R，填充得到一个满矩阵R’就是我们的目的。

 

在协同过滤中，我们通常会假设一些用户，或者一些物品属于一个类型，通过类型来推荐。这这里，我们也可以假设类（class），或者说是因子（factor）。我们假设用户对于特定的因子有一定的喜好度，并且物品对于特定的因子有一定的包含度。

比如，用户对于喜剧，武打的喜好度为1,5；而物品对于喜剧，武打的包含度为5,1；那么我们可以大概地判断用户不会喜欢这部电影。

也就是我们人为地抽象出一个隐形因子空间，然后把用户和物品分别投影到这个空间上，来直接寻找用户-物品的喜好度。

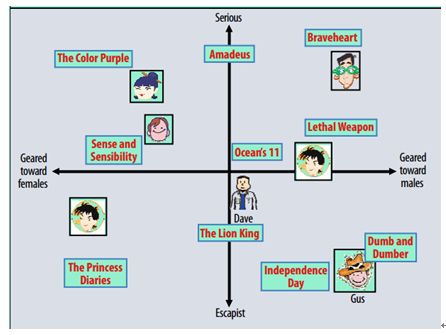
一个简单的二维隐因子空间示意图如下：

上图以男-女；轻松-严肃；两个维度作为隐因子，把用户和电影投影到这个二维空间上。

上面的问题，我们用数学的方法描述，就是写成如下的矩阵：

P表示用户对于某个隐因子的喜好度；Q表示物品对于某个隐因子的包含度。我们使用矩阵相乘得到用户-物品喜好度。

 

正如上面所说，R是一个稀疏的矩阵，我们通过R中的已知值，得到P,Q后，再相乘，反过来填充R矩阵，最后得到一个满的R矩阵。

于是隐因子模型转化为矩阵分解问题，常见的有SVD，以及下面的一些方法。

下面介绍具体的方法

 

2.      Batch learning of SVD

设已知评分矩阵V，I为索引矩阵，I（I,j）=1表示V中的对应元素为已知。U，M分别表示用户-factor，物品-factor矩阵。

于是，我们先用V分解为U*M，目标函数如下：

第一项为最小二乘误差，P可以简单理解为点乘；

第二项，第三项为防止过拟合的正则化项。

 

求解上述的优化问题，可以用梯度下降法。计算得负梯度方向如下：

我们每次迭代，先计算得到U，M的负梯度方向，然后更新U,M；多次迭代，直至收敛。

这种方法的缺点是对于大的稀疏矩阵来说，有很大的方差，要很小的收敛速度才能保证收敛。

 

改进：可以考虑加入一个动量因子，来加速其收敛速度：

 

3.      Incomplete incremental learning of SVD

上述的方法对于大的稀疏矩阵来说，不是很好的方法。

于是，我们细化求解过程。

改进后的最优化目标函数如下：

也就是，我们以V的行为单位，每次最优化每一行，从而降低batch learning的方差。

负梯度方向：

 

4.      Complete incremental learning of SVD

同样的，根据incrementlearning的减少方差的思想，我们可以再次细化求解过程。

以V的已知元素为单位，求解。

最优化目标函数如下：

 

每次迭代，我们遍历每个V中的已知元素，求得一个负梯度方向，更行U,M;

 

 

隐因子模型还有相应的其他变化版本，如compound SVD，implicit feedback SVD等，放在下一篇blog里。

参考文献：A Guide to Singular Value Decomposition for Collaborative Filtering