【Arm端算法优化笔记】一,一步步优化盒子滤波算法
1. 前言
这是我自己做的移动端算法优化笔记的第一篇文章。我入门移动端的时间其实很短,也是今年刚开始接触Neon优化并尝试用Neon来做一些算法加速工作,之前我做过系列的X86上的SSE/AVX算法加速文章分享。但那个系列已经比较久没有更新了,一是因为我日常做的都是和移动端相关的一些算法部署工作,二是因为我变懒了,所以希望新开这个专题重新找到一点分享算法优化文章的热情(笑)。关于盒子滤波这个算法的移动端优化,梁德澎作者已经有分享过一篇很优秀的文章了,即【AI移动端算法优化】二,移动端arm cpu优化学习笔记之一步步优化盒子滤波 ,所以你可能会在我的这篇文章看到很多的优化技巧已经被他讲过了,但这篇文章仍然有我自己大量的思考以及花了大量写出对应的优化代码,我接触了哪些资料或者说学习了哪些知识,我都有列举到,所以对移动端优化感兴趣的小白还是值得看看的。代码开源在https://github.com/BBuf/ArmNeonOptimization 。
2. 盒子滤波
今天要介绍的是在Arm端一步步优化盒子滤波算法,盒子滤波是最经典的滤波算法之一,常见的均值滤波算法就是盒子滤波归一化后获得结果。在原理上盒子滤波和均值滤波类似,用一个内核和图像进行卷积:
其中:
如果选择归一化,那么盒子滤波就是标准的均值滤波。
3. 原始实现
按照上面的原理,盒子滤波可以简单实现如下:
void BoxFilterOrigin(float *Src, float *Dest, int Width, int Height, int Radius){
for(int Y = 0; Y < Height; Y++){
for(int X = 0; X < Width; X++){
int ST_Y = Y - Radius;
if(ST_Y < 0) ST_Y = 0;
int EN_Y = Y + Radius;
if(EN_Y > Height-1) EN_Y = Height-1;
int ST_X = X - Radius;
if(ST_X < 0) ST_X = 0;
int EN_X = X + Radius;
if(EN_X > Width-1) EN_X = Width-1;
float sum = 0;
for(int ty = ST_Y; ty <= EN_Y; ty++){
for(int tx = ST_X; tx <= EN_X; tx++){
sum += Src[ty * Width + tx];
}
}
Dest[Y * Width + X] = sum;
}
}
}
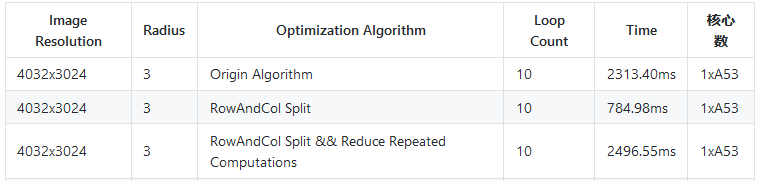
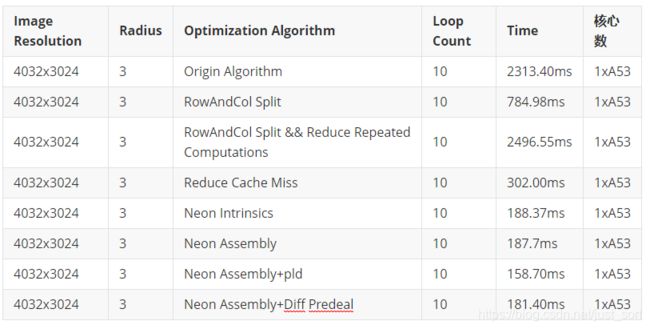
在一块Arm A53上进行测试,耗时结果如下:
2. 第一版优化
首先我们借鉴一下OpenCV在实现盒子滤波时的Trick,即利用盒子滤波是一种行列可分离的滤波,所以先进行行方向的滤波,得到中间结果,然后再对中间结果进行列方向的处理,得到最终的结果。代码实现如下:
void BoxFilterOpenCV(float *Src, float *Dest, int Width, int Height, int Radius, vector <float>&cache){
float *cachePtr = &(cache[0]);
// chuizhi
for(int Y = 0; Y < Height; Y++){
for(int X = 0; X < Width; X++){
int ST_X = X - Radius;
if(ST_X < 0) ST_X = 0;
int EN_X = X + Radius;
if(EN_X > Width-1) EN_X = Width-1;
float sum = 0;
for(int tx = ST_X; tx <= EN_X; tx++){
sum += Src[Y * Width + tx];
}
cachePtr[Y * Width + X] = sum;
}
}
//shuiping
for(int Y = 0; Y < Height; Y++){
int ST_Y = Y - Radius;
if(ST_Y < 0) ST_Y = 0;
int EN_Y = Y + Radius;
if(EN_Y > Height-1) EN_Y = Height-1;
for(int X = 0; X < Width; X++){
float sum = 0;
for(int ty = ST_Y; ty <= EN_Y; ty++){
sum += cachePtr[ty * Width + X];
}
Dest[Y * Width + X] = sum;
}
}
}
同样测一下耗时情况:
可以看到使用这种行列分离求和的技巧后,速度优化了3-4倍,但是整体耗时还是挺高的,需要继续努力。
3. 第二版优化
在上一版算法中,虽然使用行列分离技巧后降低了一些重复计算,但是并没有完全解决重复计算的问题,在行或列的单独方向上仍然存在重复计算。并且此算法的复杂度仍然和半径有关,大概复杂度为 O ( n × m × r ) O(n\times m\times r) O(n×m×r)其中 n n n为矩阵的宽度, m m m为矩阵的高度, r r r为滤波半径。实际上我们在这里再加一个Trick,就可以让算法的复杂度和半径无关了。例如对于某一行来讲,我们首先计算第一个点开头的半径范围内的和,然后对于接下来遍历到的点不需要重复计算半径区域内的和,只需要把前一个元素半径内的和,按半径窗口右/下偏移之后,减去左边移出去的点并且加上右边新增的一个点即可。这样维护这个行或者列的和就和半径无关了。
void BoxFilterOpenCV2(float *Src, float *Dest, int Width, int Height, int Radius, vector<float>&cache){
float *cachePtr = &(cache[0]);
//chuizhi
for(int Y = 0; Y < Height; Y++){
int Stride = Y * Width;
//head
float sum = 0;
for(int X = 0; X < Radius; X++){
sum += Src[Stride + X];
}
for(int X = 0; X <= Radius; X++){
sum += Src[Stride + X + Radius];
cachePtr[Stride + X] = sum;
}
//middle
for(int X = Radius+1; X <= Width-1-Radius; X++){
sum += Src[Stride + X + Radius];
sum -= Src[Stride + X - Radius - 1];
cachePtr[Stride + X] = sum;
}
//tail
for(int X = Width - Radius; X < Width; X++){
sum -= Src[Stride + X - Radius - 1];
cachePtr[Stride + X] = sum;
}
}
//shuipin
for(int X = 0; X < Width; X++){
//head
float sum = 0;
for(int Y = 0; Y < Radius; Y++){
sum += cachePtr[Y * Width + X];
}
for(int Y = 0; Y <= Radius; Y++){
sum += cachePtr[Y * Width + Radius * Width + X];
Dest[Y * Width + X] = sum;
}
//middle
for(int Y = Radius+1; Y <= Height-1-Radius; Y++){
sum += cachePtr[Y * Width + Radius * Width + X];
sum -= cachePtr[Y * Width - (Radius + 1) * Width + X];
Dest[Y * Width + X] = sum;
}
//tail
for(int Y = Height-Radius; Y < Height; Y++){
sum -= cachePtr[Y * Width - (Radius + 1) * Width + X];
Dest[Y * Width + X] = sum;
}
}
}
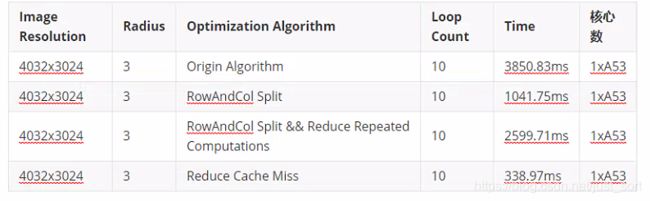
理论上来说,这版优化的速度比第一版要快很多吧?我们来测一下速:
现在发生了一个非常奇怪的事情,虽然计算量变少了,但是耗时甚至比原始实现还多了?这是为什么呢?
4. 第三版优化 减少Cache Miss
在上一版优化中,我们在列方向上的处理方式和行方向上完全相同。但由于CPU架构的一些原因(主要是Cache Miss的增加),同样的算法沿着列方向处理总是会比按照行方向慢一个档次,因此在上面的第二版优化中由于频繁的在列方向进行操作(这个操作的跨度还比较大,比如第 Y Y Y行会访问第 Y − R a d i u s − 1 Y-Radius-1 Y−Radius−1行的元素)使得算法速度被严重拖慢,解决这个问题的方法有很多,例如:先对中间结果进行转置,然后再按照行方向的规则进行处理,处理完后在将数据转置回去,但是矩阵转置相对比较麻烦。还有一种方法是OpenCV代码实现中展示的,即用了一个大小是 W i d t h Width Width的向量colSum,来存储某一行对应点的列半径区域内的和,然后遍历的时候还是按照行来遍历,中间部分对colSum的更新也是减去遍历跑出去的一行,加上进来的一行,这样就可以减少Cache Miss。
这部分的代码实现如下:
void BoxFilterCache(float *Src, float *Dest, int Width, int Height, int Radius, vector<float>&cache){
float *cachePtr = &(cache[0]);
//chuizhi
for(int Y = 0; Y < Height; Y++){
int Stride = Y * Width;
//head
float sum = 0;
for(int X = 0; X < Radius; X++){
sum += Src[Stride + X];
}
for(int X = 0; X <= Radius; X++){
sum += Src[Stride + X + Radius];
cachePtr[Stride + X] = sum;
}
//middle
for(int X = Radius+1; X <= Width-1-Radius; X++){
sum += Src[Stride + X + Radius];
sum -= Src[Stride + X - Radius - 1];
cachePtr[Stride + X] = sum;
}
//tail
for(int X = Width - Radius; X < Width; X++){
sum -= Src[Stride + X - Radius - 1];
cachePtr[Stride + X] = sum;
}
}
vector <float> colsum;
colsum.resize(Width);
float *colsumPtr = &(colsum[0]);
for(int X = 0; X < Width; X++){
colsumPtr[X] = 0;
}
//shuipin
for(int Y = 0; Y < Radius; Y++){
int Stride = Y * Width;
for(int X = 0; X < Width; X++){
colsumPtr[X] += colsumPtr[Stride + X];
}
}
//head
for(int Y = 0; Y <= Radius; Y++){
int Stride = Y * Width;
for(int X = 0; X < Width; X++){
colsumPtr[X] += cachePtr[(Y + Radius) * Width + X];
Dest[Stride + X] = colsumPtr[X];
}
}
//middle
for(int Y = Radius+1; Y <= Height-1-Radius; Y++){
int Stride = Y * Width;
for(int X = 0; X < Width; X++){
colsumPtr[X] += cachePtr[(Y + Radius) * Width + X];
colsumPtr[X] -= cachePtr[(Y - Radius - 1) * Width + X];
Dest[Stride + X] = colsumPtr[X];
}
}
//tail
for(int Y = Height-Radius; Y < Height; Y++){
int Stride = Y * Width;
for(int X = 0; X < Width; X++){
colsumPtr[X] -= cachePtr[(Y - Radius - 1) * Width + X];
Dest[Stride + X] = colsumPtr[X];
}
}
}
可以看到速度相比于第一版又优化了3倍,所以我们这个减少Cache Miss的技巧是行之有效的。
5. 第四版优化 Neon Intrinsics
接下来我们试一下使用Neon Intrinsics来优化一下这个算法,关于Neon指令集的编写入门可以看这篇文章:【AI移动端算法优化】五,移动端arm cpu优化学习笔记之内联汇编入门 。
在行方向上由于相邻元素有依赖关系,因此是无法并行的,所以我们可以在列方向上使用Neon Intrinsics来并行处理数据。
由于这里代码实现比较长,所以我只贴出一段原始实现和改写后的Neon Intrinsics实现,完整代码可以在https://github.com/BBuf/ArmNeonOptimization/blob/master/src/boxFilter.cpp 中找到。贴出列方向求和部分的head的原始实现和改写成Neon Intrinsics后的实现:
int Block = Width >> 2;
int Remain = Width - (Block << 2);
//Origin
// for(int Y = 0; Y < Radius; Y++){
// int Stride = Y * Width;
// for(int X = 0; X < Width; X++){
// colsumPtr[X] += colsumPtr[Stride + X];
// }
// }
for(int Y = 0; Y < Radius; Y++){
int Stride = Y * Width;
float* tmpColSumPtr = colsumPtr;
float* tmpCachePtr = cachePtr;
int n = Block;
int re = Remain;
for(; n > 0; n--){
float32x4_t colsum = vld1q_f32(tmpColSumPtr);
float32x4_t cache = vld1q_f32(tmpCachePtr);
float32x4_t sum = vaddq_f32(colsum, cache);
vst1q_f32(tmpColSumPtr, sum);
tmpColSumPtr += 4;
tmpCachePtr += 4;
}
for (; re > 0; re--) {
*tmpColSumPtr += *tmpCachePtr;
tmpColSumPtr ++;
tmpCachePtr ++;
}
}
这个代码也比较好懂,v1d1q_f32代表同时加载4个浮点数,然后vaddq_f32代表将两个float32x4_t的向量相加,即同时处理了4个浮点数,然后再把结果用vst1q_fp32写回内存,并且把参与运算的指针地址移动4个单位。下面转载了一个Neon指令集书写格式的解释可以更好的帮助大家理解。
下方代码块转自:http://blog.csdn.net/charleslei/article/details/52698220
NEON 内置函数命名方式有两种,分别对应源操作数是否涉及标量,具体解释如下。
1)源操作数涉及标量时,数据类型表示为v op dt_n/lane_type。
其中:
①n表示源操作数是标量而返回向量,lane 表示运算涉及向量的一个元素。
②op表示操作,如dup、add、sub、mla等。
③dt是目标向量和源向量长度表示符。
如果目标向量和源向量长度都为64位,dt为空。
如果源向量和目标向量长度一致都为128位,dt为q。
如果目标向量长度比源数向量长度大,且源向量长度都为 64 位、目标向量长度为 128 位,dt为 l(英文字母,不是数字1)。
如果多个源向量长度不一致且都不大于目标向量长度(一个源向量长度为 64 位,另一个为 128 位,目标向量长度为 128 位),dt为 w。
如果目标向量长度比源向量长度小,即目标向量长度dt为 n。
④type表示源数据类型缩写,如u8 表示 uint8;u16 表示 uint16;u32 表示 uint32;s8 表示 int8;s16 表示 int16;s32 表示 int32;f32 表示 float32。
2)源操作数全是向量时,数据类型表示为v op dt_type,其中op、dt和type的含义和源操作数为标量时一致。
下面给出几个实例以增加读者理解。
1)内置函数vmla_f32表示使用64位向量寄存器操作32位浮点数据,即源操作数使用的向量寄存器和目标操作数使用的向量寄存器表示都是float32x2_t。
2)内置函数vmlaq_f32表示使用128位向量寄存器操作32位浮点数据,即源操作数使用的向量寄存器和目标操作数使用的向量表示都是float32x4_t。
3)内置函数vmlal_u32表示使用的目标寄存器是128位向量,源寄存器是64位向量,操作32位无符号整数。
4)内置函数vaddw_s32表示使用的目标寄存器是128位向量,源寄存器一个是64位向量,一个是128位向量。
5)内置函数vmovn_u64表示目标寄存器是64位向量,源寄存器是128位向量,即同时操作两个数。
然后我们再测一下这一版的耗时情况:
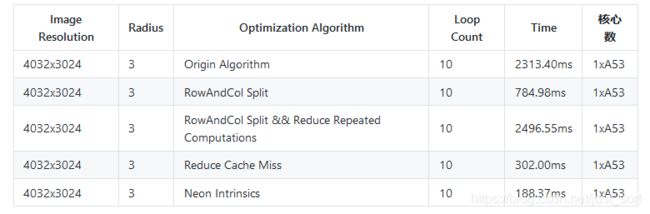
可以看到使用Neon Intrinsics之后,速度又有了进一步提升,接下来的一步需要向Neon Assembly以及调度板子上拥有的2块A53角度去分析了。
关于更多的Intrinsics指令可以在下面的文档中查询到:https://static.docs.arm.com/den0018/a/DEN0018A_neon_programmers_guide_en.pdf 。
6. 内联汇编入门
在上面我们用C++写了上层代码,同时也写了一版Neon Intrinsics来处理盒子滤波算法。但实际上,无论是上面的哪种写法在程序编译之后都会变成更底层的汇编指令。这些汇编指令可以控制寄存器完成数据读取,数据计算,数据存储整个流程。而仅仅依靠编译器的自动优化有时候是不够的,甚至编译器在某些特殊硬件或者一些特殊逻辑上进行负优化。基于此,做算法优化的人员就需要自己手动操作寄存器来优化数据读写,数据计算,甚至指令重排来完成进一步加速。
我是一个小白,这里也是我写的第一份Neon内联汇编代码,所以我们还是先大概讲一下寄存器的概念以及内联汇编的基本格式,这对后面理解代码至关重要。
6.1 armv7/v8 寄存器介绍
ARM是微处理器行业的一家知名企业,其芯片结构有:armv5、armv6、armv7和armv8系列。芯片类型有:arm7、arm9、arm11、cortex系列。指令集有:armv5、armv6和neon指令。具体可以参考:http://baike.baidu.com/view/11200.htm 。
目前经常使用到的一些用于移动端算法开发的芯片如华为Hisi系列,RK系列一般都是采用armv7/v8结构。所以我们以这两种Arm架构出发来科普一下通用寄存器和向量寄存器。
通用寄存器
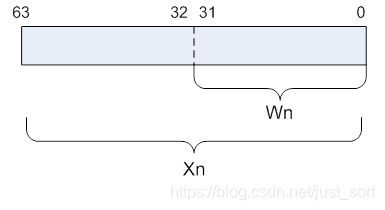
armv7有16个32-bit的通用寄存器,用R0-R15来表示,而armv8有31个64-bit的通用寄存器,用X0-X30 来表示,还有一个不同名字的特殊寄存器,用途取决于上下文,,因此我们可以看成 31个64位的X寄存器或者31个32位的W寄存器(X寄存器的低32位)。如下图所示:
向量寄存器
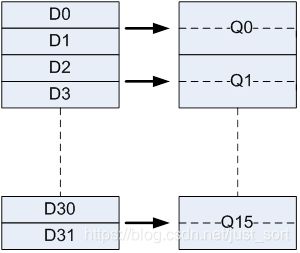
armv7包含16个128-bit的向量寄存器,用Q0-Q15来表示,其中每个寄存器又可以当作两个64-bit的向量寄存器来使用,用D0-D31来表示,对应关系为:
Q n = ( D n ∗ 2 , D n ∗ 2 + 1 ) Q_n=(D_{n*2},D_{n*2+1}) Qn=(Dn∗2,Dn∗2+1)
即D寄存器的偶数下标对应着此下标的Q寄存器的低64-bit,而奇数下标则对应着此下标的Q寄存器的高64-bit。对应关系如下图所示:
对于armv8则有32个128-bit的向量寄存器(可以想一下SSE和AVX的对应关系,道理是一样的)用V0-V31来表示,其表达形式相比armv7则更加灵活,如下图所示:
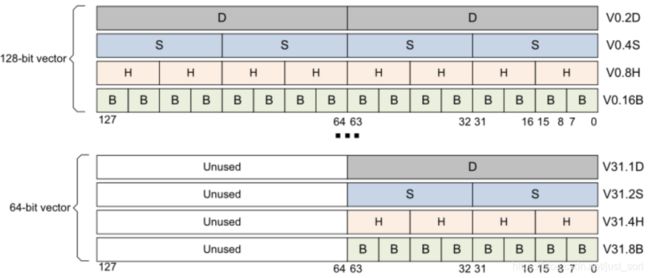
从上图的上半部分来看,每一个128-bit的V寄存器都可以当做
- 2个64-bit的向量寄存器,用Vn.2D来表示,注意n代表寄存器的下标,图中展示了0和31两种情况。
- 4个32-bit的向量寄存器,用Vn.4S来表示。
- 8个16-bit的向量寄存器,用Vn.8H来表示。
- 16个8-bit的向量寄存器,用Vn.16B来表示。
从下半部分来看,每一个128-bit的V寄存器都可以只用低64-bit,这样每一个V寄存器也可以看作:
- 1个64-bit的向量寄存器,用Vn.1D来表示。
- 2个32-bit的向量寄存器,用Vn.2S来表示。
- 4个16-bit的向量寄存器,用Vn.4H来表示。
- 8个8-bit的向量寄存器,用Vn.8B来表示。
6.2 内联汇编一般格式
了解了一下通用寄存器和向量寄存器之后我们可以来看一下Arm内联汇编代码编写的一般格式,这个文档说的很清楚:https://gcc.gnu.org/onlinedocs/gcc/Extended-Asm.html#Extended-Asm ,这里翻译一下。
内联汇编代码的一般格式可以表示如下:
asm asm-qualifiers ( AssemblerTemplate
: OutputOperands
: InputOperands
: Clobbers)
其中:
-
AssemblerTemplate:代表我们需要自己实现的汇编代码部分。
-
OutputOperands: 代表在内联汇编中会被修改的变量列表,变量之间用逗号隔开。然后每个变量的格式表示为:
[asmSymbolicName] "constraint"(cvariablename),其中:- cvariablename:表示变量原始的名字。
- asmSymbolicName:表示变量在内联汇编代码中的别名,一般和cvariablename一样,在汇编代码部分就可以通过
%[asmSymbolicName]去使用这个变量。 - constraint:这个比较复杂可以填的参数很多,例如填
r就表示如果寄存器操作数在通用寄存器中,则允许使用该操作数。更详细可以看https://gcc.gnu.org/onlinedocs/gcc/Extended-Asm.html#OutputOperands。
-
InputOperands : 代表在内联汇编中用到的所有变量列表(包含会被修改和无须修改的),变量之间仍用逗号隔开。每个变量的格式为:
[asmSymbolicName] "constraint"(cexpression)。和上面介绍的OutputOperands 不一样的地方在于,首先需要按照OutputOperands列表的顺序将变量再列一遍,但是constraint用数字代替从0开始,然后才是写其他只读变量,只读变量constraint填r。 -
Clobbers:一般以
"cc", "memory"开头,然后接着填内联汇编中用到的通用寄存器和向量寄存器。其中cc表示内联汇编代码修改了标志寄存器,而memory则通知GCC当前内联汇编语句可能会对某些寄存器或内存进行修改,希望GCC在编译时能够将这一点考虑进去。
我们看一下NCNN的absval算子在arm端的实现代码:
#if __ARM_NEON
int nn = size >> 2;
int remain = size - (nn << 2);
#else
int remain = size;
#endif // __ARM_NEON
#if __ARM_NEON
#if __aarch64__
if (nn > 0)
{
asm volatile(
"0: \n"
"prfm pldl1keep, [%1, #128] \n"
"ld1 {v0.4s}, [%1] \n"
"fabs v0.4s, v0.4s \n"
"subs %w0, %w0, #1 \n"
"st1 {v0.4s}, [%1], #16 \n"
"bne 0b \n"
: "=r"(nn), // %0
"=r"(ptr) // %1
: "0"(nn),
"1"(ptr)
: "cc", "memory", "v0");
}
#else
if (nn > 0)
{
asm volatile(
//汇编代码部分
"0: \n"
"vld1.f32 {d0-d1}, [%1] \n"
"vabs.f32 q0, q0 \n"
"subs %0, #1 \n"
"vst1.f32 {d0-d1}, [%1]! \n"
"bne 0b \n"
//OutputOperands
: "=r"(nn), // %0
"=r"(ptr) // %1
//InputOperands
: "0"(nn),
"1"(ptr)
//Clobbers 这里只有q0这个向量寄存器
: "cc", "memory", "q0");
}
#endif // __aarch64__
#endif // __ARM_NEON
for (; remain > 0; remain--)
{
*ptr = *ptr > 0 ? *ptr : -*ptr;
ptr++;
}
}
可以看到到里的实现这和上面介绍的内联汇编一般形式是一致的。我们可以来解释一下这段汇编代码,其中 "vld1.f32 {d0-d1}, [%1] \n"表示从ptr这个地址连续读取4个浮点数到{d0-d1}也就是q0寄存器,浮点数每个32位,乘以四就是128位。然后"vabs.f32 q0, q0 \n"就是将q0寄存器中的数取绝对值操作(这里是实现的NCNN中的AbsVal OP)。然后"subs %0, #1 \n"代表将nn减一然后然后bne判断是否为0, 不为0则继续循环跳到开头0标记出继续执行。再bne这行代码之前还有一行是"vst1.f32 {d0-d1}, [%1]! \n",这代表把寄存器的内容存到ptr指向的内存里面。
7. 第五版优化 Neon内联汇编
有了上面的铺垫,我们就不难写出内联汇编版本的盒子滤波代码了,我这里只改写了水平方向求和的中间部分,因为这部分是最耗时的(头尾两部分求和的矩阵的宽度都只有一个Radius这么大),如果需要改写头尾两部分也可以直接参考这个代码,代码实现如下:
int n = Block;
int re = Remain;
// for(; n > 0; n--){
// float32x4_t colsum = vld1q_f32(tmpColSumPtr);
// float32x4_t add = vld1q_f32(tmpaddPtr);
// float32x4_t sub = vld1q_f32(tmpsubPtr);
// float32x4_t sum = vaddq_f32(colsum, add);
// sum = vsubq_f32(sum, sub);
// vst1q_f32(tmpColSumPtr, sum);
// vst1q_f32(tmpDestPtr, sum);
// tmpaddPtr += 4;
// tmpsubPtr += 4;
// tmpColSumPtr += 4;
// tmpDestPtr += 4;
// }
// 我的翻译顺序为OutputOperands->InputOperands->汇编代码->Clobbers
asm volatile(
"0: \n" //开头0标记,类似do while中的while(n>0)里的0
"vld1.s32 {d0-d1}, [%0]! \n" //表示从tmpaddPtr这个地址连续读取4个浮点数到{d0-d1}也就是q0寄存器
//浮点数每个32位,乘以四就是128位。最后感叹号表示,这个指令完成之后
//tmpaddPtr地址加4的意思,没有就是不变。,和上面代码对应
"vld1.s32 {d2-d3}, [%1]! \n" //同理,处理tmpsubPtr,放到q1寄存器
"vld1.s32 {d4-d5}, [%2] \n" //同理,处理tmpColSumPtr,放到q2寄存器,由于tmpColSumPtr要改变值
//,所以暂时不移动地址,等待计算完成再移动
"vadd.f32 q4, q0, q2 \n" //对应float32x4_t sum = vaddq_f32(colsum, add);
"vsub.f32 q3, q4, q1 \n" //对应sum = vsubq_f32(sum, sub);
"vst1.s32 {d6-d7}, [%3]! \n" //把寄存器的内容存到tmpDestPtr地址指向的内存
"vst1.s32 {d6-d7}, [%2]! \n" //把寄存器的内容存到tmpColSumPtr地址指向的内存
"subs %4, #1 \n" //n-=1
"bne 0b \n" //bne判断nn是否为0, 不为0则继续循环跳到开头0标记出继续执行
// OutputOperands
: "=r"(tmpaddPtr),
"=r"(tmpsubPtr),
"=r"(tmpColSumPtr),
"=r"(tmpDestPtr),
"=r"(n)
// InputOperands
: "0"(tmpaddPtr),
"1"(tmpsubPtr),
"2"(tmpColSumPtr),
"3"(tmpDestPtr),
"4"(n)
//Clobbers 这里用到了q0,q1,q2,q3,q4这五个向量寄存器
: "cc", "memory", "q0", "q1", "q2", "q3", "q4"
);
每一行代码都添加了注释,实现起来其实并不难,但是问题是这个好像并没有什么加速效果?速度测试如下:
可以看到改写了内联汇编之后速度没有加快呢,那么问题出在哪呢,或者说改写内联汇编之后相比Neon Intrinsics速度一定能变快吗?
8. 第六版优化 ARM中的预取命令pld的使用
在阅读NCNN的arm端卷积算子内联汇编时发现pld这个指令被大量应用,然后查询了一下,功能如下:
pld,即预读取指令,pld指令只在armv5以上版本有效。使用pld指令可以提示ARM预先把cache line填充好。pld指令中的offset很有讲究。一般为64-byte的倍数。
功能:cache预读取(PLD,PreLoad),使用pld指示存储系统从后面几条指令所指定的存储器地址读取,存储系统可使用这种方法加速以后的存储器访问。
格式:pld[Rn,{offset}]
其中:
Rn 存储器的基址寄存器。
Offset 加在Rn上的偏移量。
所以一个简单的想法是直接将pld指令放到vld1.s32看看是否有性能上的提升?代码稍加修改如下:
// 我的翻译顺序为OutputOperands->InputOperands->汇编代码->Clobbers
asm volatile(
"0: \n" //开头0标记,类似do while中的while(n>0)里的0
"pld [%0, #128] \n"
"vld1.s32 {d0-d1}, [%0]! \n" //表示从tmpaddPtr这个地址连续读取4个浮点数到{d0-d1}也就是q0寄存器
//浮点数每个32位,乘以四就是128位。最后感叹号表示,这个指令完成之后
//tmpaddPtr地址加4的意思,没有就是不变。,和上面代码对应
"pld [%1, #128] \n"
"vld1.s32 {d2-d3}, [%1]! \n" //同理,处理tmpsubPtr,放到q1寄存器
"pld [%2, #128] \n"
"vld1.s32 {d4-d5}, [%2] \n" //同理,处理tmpColSumPtr,放到q2寄存器,由于tmpColSumPtr要改变值
//,所以暂时不移动地址,等待计算完成再移动
"vadd.f32 q4, q0, q2 \n" //对应float32x4_t sum = vaddq_f32(colsum, add);
"vsub.f32 q3, q4, q1 \n" //对应sum = vsubq_f32(sum, sub);
"vst1.s32 {d6-d7}, [%3]! \n" //把寄存器的内容存到tmpDestPtr地址指向的内存
"vst1.s32 {d6-d7}, [%2]! \n" //把寄存器的内容存到tmpColSumPtr地址指向的内存
"subs %4, #1 \n" //n-=1
"bne 0b \n" //bne判断nn是否为0, 不为0则继续循环跳到开头0标记出继续执行
// OutputOperands
: "=r"(tmpaddPtr),
"=r"(tmpsubPtr),
"=r"(tmpColSumPtr),
"=r"(tmpDestPtr),
"=r"(n)
// InputOperands
: "0"(tmpaddPtr),
"1"(tmpsubPtr),
"2"(tmpColSumPtr),
"3"(tmpDestPtr),
"4"(n)
//Clobbers 这里用到了q0,q1,q2,q3,q4这五个向量寄存器
: "cc", "memory", "q0", "q1", "q2", "q3", "q4"
);
再测一下速度,结果如下:
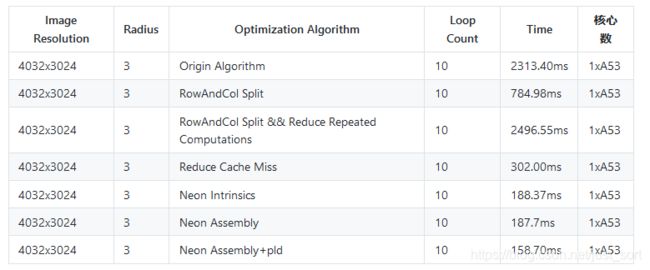
可以看到加入pld之后,速度又提升了20ms!说明之前改写的汇编版本直接在内存和寄存器之间读写数据的确过于耗时。
9. 第七版优化
然后我又想到了一个方法,不知道是否有效,那就是将上面的差值先处理一遍,然后再叠加到结果上,即将下面这个代码中的add-sub先计算出来存成diff(diff=add-sub),然后将结果加上这个diff即可:
for(; n > 0; n--){
float32x4_t colsum = vld1q_f32(tmpColSumPtr);
float32x4_t add = vld1q_f32(tmpaddPtr);
float32x4_t sub = vld1q_f32(tmpsubPtr);
float32x4_t sum = vaddq_f32(colsum, add);
sum = vsubq_f32(sum, sub);
vst1q_f32(tmpColSumPtr, sum);
vst1q_f32(tmpDestPtr, sum);
tmpaddPtr += 4;
tmpsubPtr += 4;
tmpColSumPtr += 4;
tmpDestPtr += 4;
}
改写一下第六版中的汇编代码如下:
//处理出所有的差值
asm volatile(
"0: \n" //开头0标记,类似do while中的while(n>0)里的0
"pld [%0, #128] \n"
"vld1.s32 {d0-d1}, [%0]! \n"
"pld [%1, #128] \n"
"vld1.s32 {d2-d3}, [%1]! \n"
"vsub.f32 q2, q0, q1 \n"
"vst1.s32 {d4-d5}, [%2]! \n"
"subs %3, #1 \n"
"bne 0b \n"
// OutputOperands
: "=r"(tmpaddPtr),
"=r"(tmpsubPtr),
"=r"(tmpDiffPtr),
"=r"(nn)
// InputOperands
: "0"(tmpaddPtr),
"1"(tmpsubPtr),
"2"(tmpDiffPtr),
"3"(nn)
//Clobbers 这里用到了q0,q1,q2这三个向量寄存器
: "cc", "memory", "q0", "q1", "q2"
);
for(;ree > 0; ree--){
*tmpDiffPtr = *tmpaddPtr - *tmpsubPtr;
tmpaddPtr++;
tmpDiffPtr++;
tmpsubPtr++;
}
//把差加回去
asm volatile(
"0: \n"
"pld [%0, #128] \n"
"vld1.s32 {d0-d1}, [%0]! \n"
"pld [%1, #128] \n"
"vld1.s32 {d1-d2}, [%1] \n"
"vadd.f32 q2, q0, q1 \n"
"vst1.s32 {d4-d5}, [%1]! \n"
"vst1.s32 {d4-d5}, [%2]! \n"
"subs %3, #1 \n" //n-=1
"bne 0b \n"
// OutputOperands
: "=r"(tmpDiffPtr),
"=r"(tmpColSumPtr),
"=r"(tmpDestPtr),
"=r"(n)
// InputOperands
: "0"(tmpDiffPtr),
"1"(tmpColSumPtr),
"2"(tmpDestPtr),
"3"(n)
//Clobbers 这里用到了q0,q1,q2这三个向量寄存器
: "cc", "memory", "q0", "q1", "q2"
);
for(;re > 0; re--){
*tmpColSumPtr += *tmpDiffPtr;
*tmpDestPtr += *tmpDiffPtr;
tmpDiffPtr++;
tmpDestPtr++;
tmpColSumPtr++;
}
测一下速度:
可以看到它比第6个版本还慢一些,似乎做了负优化,这是为什么呢?个人猜测是寄存器的频繁读取导致的,为了验证一下这个想法,我只使用2个寄存器,即把上面2段代码的q2改成q0,然后测一下速度:
可以看到整个耗时变成了170ms,减少了11ms,所以分段计算又带来了一个新问题,就是指令频繁存取数据可能增加更多耗时。所以这时候再回去看第六版的代码是否可以减少寄存器的使用以减少寄存器和内存之间通信带来的耗时,但仔细观察发现寄存器似乎已经没有可以再减少的了,所以这版优化宣告失败QAQ。
10. 第八版优化 双发射流水线
从德彭作者那里发现了另外一种优化方法,就是说当代的CPU处理器都是支持双发射流水线的,即在同一时刻可以发射两条指令,那么显然我们可以利用这个特性来进行加速。关于CPU指令执行及流水线(超标量、多发射、乱序执行)可以看一下这篇文章https://blog.csdn.net/qq_41154905/article/details/105163718,我就不再赘述了。代码编写的基本思路就是把两条vadd.f32指令放一起,然后跟两条vsub.f32,然后这里有一个关键的问题,那就是
"pld [%1, #256] \n"
"vld1.s32 {d4-d7}, [%1]! \n" //q2,q3
这行指令应该放在哪里?我们先放在两个vadd.fd32后面测一下速度,这部分代码为:
asm volatile(
"0: \n"
"pld [%0, #256] \n"
"vld1.s32 {d0-d3}, [%0]! \n" //q0,q1
"pld [%2, #256] \n"
"vld1.s32 {d8-d11}, [%2] \n" //q4,q5
"vadd.f32 q6, q0, q4 \n"
"vadd.f32 q7, q1, q5 \n"
"pld [%1, #256] \n"
"vld1.s32 {d4-d7}, [%1]! \n" //q2,q3
"vsub.f32 q6, q6, q2 \n"
"vsub.f32 q7, q7, q3 \n"
"vst1.s32 {d12-d15}, [%3]! \n"//q8, q9
"vst1.s32 {d12-d15}, [%2]! \n"
"subs %4, #1 \n"
"bne 0b \n"
// OutputOperands
: "=r"(tmpaddPtr),
"=r"(tmpsubPtr),
"=r"(tmpColSumPtr),
"=r"(tmpDestPtr),
"=r"(n)
// InputOperands
: "0"(tmpaddPtr),
"1"(tmpsubPtr),
"2"(tmpColSumPtr),
"3"(tmpDestPtr),
"4"(n)
//Clobbers 这里用到了q0,q1,q2,q3,q4这五个向量寄存器
: "cc", "memory", "q0", "q1", "q2", "q3", "q4", "q5", "q6", "q7", "q8", "q9"
);
速度测试结果如下:
看最后一栏,使用这个优化之后目前速度达到了最优。那么我们调整一下指令的顺序,将"vld1.s32 {d4-d7}, [%1]! \n" //q2,q3放到第一个vadd.f32之后来测一下速度:
可以看到速度只有微小的差距,说明在这个代码中的指令重排没有多大效果,可能是因为计算的等待时间比较少的原因,但在其它的一些算法中例如同时计算A=B+C以及D=E+F这种逻辑中指令重排就会获得更多的加速收益。
11. 一些其它的可能优化方法
前面提到过,我们可以将矩阵转置,然后原矩阵的行方向的求和仍然可以用指令集来计算,转置也可以用指令集来优化,只要转置的速度小于在行方向也进行并行计算带来的加速,那么算法仍然会获得速度增加。这个实验暂时我还没做,如果后面做了,后面会考虑放出实验结果的。
欢迎交流讨论其它可能的优化方法…
12. 参考
- https://blog.csdn.net/ce123_zhouwei/article/details/8471614
- https://blog.csdn.net/qq_21125183/article/details/80590934
- https://mp.weixin.qq.com/s/I_qSUlX9uRhCacE1cThtuA
- https://blog.csdn.net/qq_41154905/article/details/105163718
- https://blog.csdn.net/u013099854/article/details/105664575/
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
![]()
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
![]()