2019 CCPC 秦皇岛 Escape 最大流

Problem Description

给一个 n×m 大小的迷宫，左上角为 (1,1) ，右下角为 (n,m) 。迷宫中的每个 1×1 的格子要么是障碍，要么为空。

有 a 个机器人要从迷宫上方走到迷宫下方，其中第 i 个机器人的初始位置为 (1,pi) 的正上方，不妨记为 (0,pi) ，初始运动方向为向下，即 (1,0) 。

迷宫有 b 个出口，其中第 i 个出口位于 (n,ei) 的正下方，不妨记为 (n+1,ei) 。

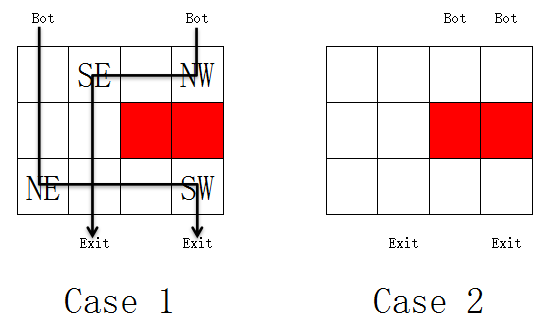
现在你想要让这些机器人走出迷宫，但是这些机器人只会沿着当前的运动方向走，不会转弯，所以你需要在迷宫中的某些空格子上设置转弯装置，每个格子上最多只能有一个转弯装置，转弯装置有 ``NW'',``NE'',``SW'',``SE'' 4 种，其中：

• "NW'' 装置会把从格子上方走来的机器人的运动方向变成向左，以及把从格子左方走来的机器人的运动方向变成向上，不允许机器人从格子的右方及下方进入。
  
• "NE'' 装置会把从格子上方走来的机器人的运动方向变成向右，以及把从格子右方走来的机器人的运动方向变成向上，不允许机器人从格子的左方及下方进入。
  
• "SW'' 装置会把从格子下方走来的机器人的运动方向变成向左，以及把从格子左方走来的机器人的运动方向变成向下，不允许机器人从格子的右方及上方进入。
  
• "SE'' 装置会把从格子下方走来的机器人的运动方向变成向右，以及把从格子右方走来的机器人的运动方向变成向下，不允许机器人从格子的左方及上方进入。
  
  
   
• 你想知道，是否存在一种设置转弯装置的方案，使得所有机器人都能在不经过障碍格子以及不非法进入转弯装置的情况下走出迷宫（允许多个机器人经过同一个格子）。能则输出 ``Yes''，不能则输出 ``No''。

 

 

Input

输入第一行一个正整数 T ，表示数据组数。

对于每组数据：

第一行四个正整数 n,m,a,b ，表示迷宫的大小，机器人个数，出口个数。

接下来 n 行，每行一个长为 m 的 01 字符串 si ，表示迷宫，其中第 i 个字符串的第 j 个字符表示迷宫中 (i,j) 的状态 —— 0 表示为空，1 表示为障碍。

接下来一行 a 个互不相同的正整数 pi ，表示机器人的初始位置 (0,pi) 。

接下来一行 b 个互不相同的正整数 ei ，表示出口的位置 (n+1,ei) 。

1≤T≤10

1≤n,m≤100,1≤a,b,pi,ei≤m

 

 

Output

输出共 T 行，每行一个字符串 ``Yes'' 或者 ``No''，表示对应数据的答案。

 

 

Sample Input

2 3 4 2 2 0000 0011 0000 1 4 2 4 3 4 2 2 0000 0011 0000 3 4 2 4

 

 

Sample Output

Yes No

Hint

#include 
using namespace std;
#define ll long long
#define INF 0x7ffffff
#define sz(i,j) n*m+(i-1)*m+j
#define sp(i,j) (i-1)*m+j 
const int M = 1000005;
const int inf = 0x7fffffff;
struct E {
    int nxt,u,v,w;
};
E edg[M];
int d[M],head[M],cnt;
int s,t,n,m;
void init() {
    cnt = 0;
    memset(head,-1,sizeof head);
}
void add(int u,int v,int w) {
    edg[cnt].v = v;
    edg[cnt].u = u;
    edg[cnt].w = w;
    edg[cnt].nxt = head[u];
    head[u] = cnt++;
    edg[cnt].v = u;
    edg[cnt].u = v;
    edg[cnt].w = 0;
    edg[cnt].nxt = head[v];
    head[v] = cnt++;
}
bool bfs(int s,int t) {
    queue q;
    memset(d,0,sizeof d);
    q.push(s);
    d[s] = 1;
    while(!q.empty()) {
        int top = q.front();
        q.pop();
        for(int i = head[top]; i + 1; i = edg[i].nxt) {
            int v = edg[i].v,w = edg[i].w;
            if(!d[v] && w) {
                d[v] = d[top] + 1;
                q.push(v);
            }
        }
    }
    return d[t] > 0;
}
int dfs(int s,int t,int inflow) {
    if(s == t || !inflow) return inflow;
    int flow = 0;
    for(int i = head[s]; i + 1; i = edg[i].nxt) {
        int v = edg[i].v,w = edg[i].w;
        if(w && d[v] == d[s] + 1) {
            int x = dfs(v,t,min(inflow,w));
            edg[i].w -= x;
            edg[i ^ 1].w += x;
            inflow -= x;
            flow += x;
            if(!inflow) break;
        }
    }
    if(!flow) d[s] = -2;
    return flow;
}
long long dinic(int s,int t) {
    long long ans = 0;
    while(bfs(s,t))
        ans += dfs(s,t,inf);
    return ans;
}
bool vis[105][105];
char ch[105];
int main() {
    int a,b,c;
    int _;
    int num1,num2;
    for(scanf("%d",&_); _; _--) {
        scanf("%d %d %d %d",&n,&m,&num1,&num2);
        init();
        s = n*m*2+5;    t = s+1;
        ll ans = 0;
        for(int i=1; i<=n; i++) {
            scanf("%s",ch);
            for(int j=1;j<=m;j++){
                int p1 = sz(i,j);    
                int p2 = sp(i,j);
                if(ch[j-1]=='0'){
                    if(i-1>=1)add(p1,sz(i-1,j),1);
                    if(i+1<=n)add(p1,sz(i+1,j),1);
                    if(j-1>=1)add(p2,sp(i,j-1),1);
                    if(j+1<=m)add(p2,sp(i,j+1),1);
                    add(p1,p2,1);    add(p2,p1,1);
                }
            } 
        }
        int u;
        for(int i=1;i<=num1;i++){
            scanf("%d",&u);
            u = sz(1,u);
            add(s,u,1);
        }
        for(int i=1;i<=num2;i++){
            scanf("%d",&u);
            u = sz(n,u);
            add(u,t,inf);
        }
        if(dinic(s,t)==num1){
            printf("Yes\n");
        }else {
            printf("No\n");
        }
    }
    return 0;
}