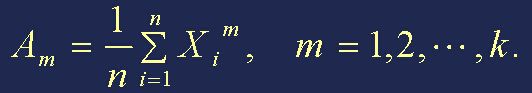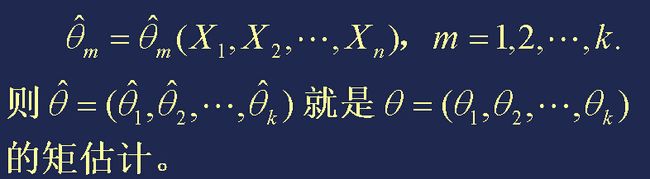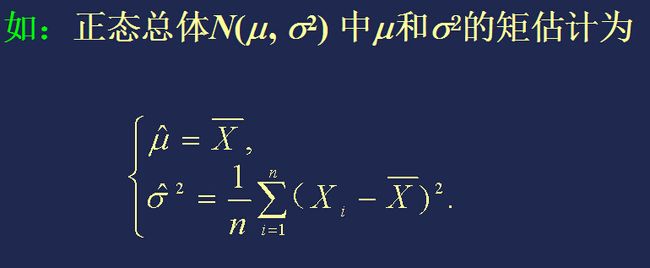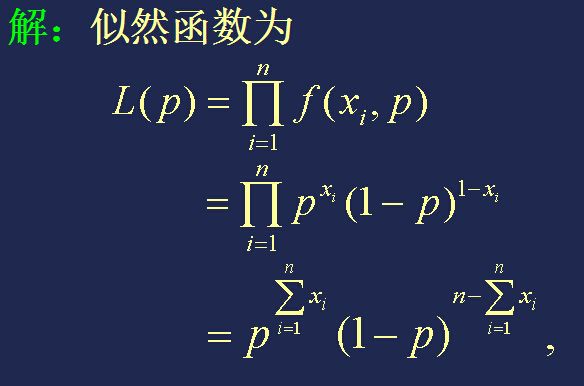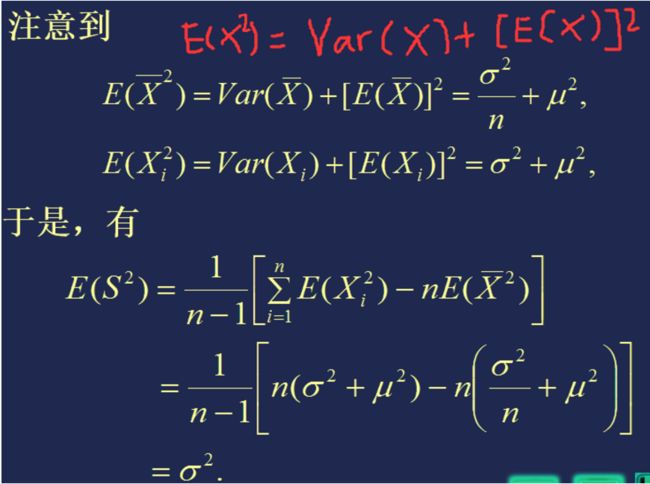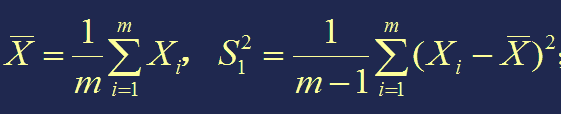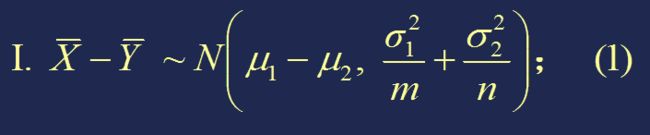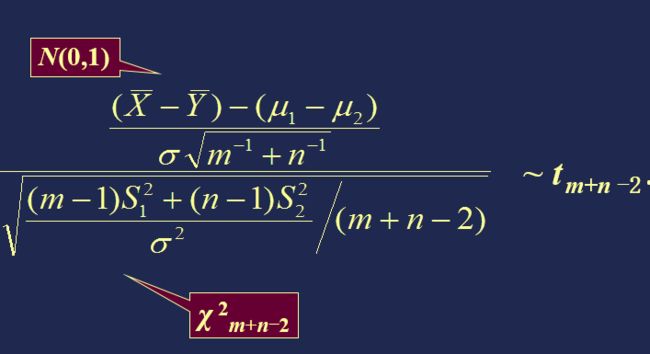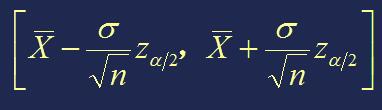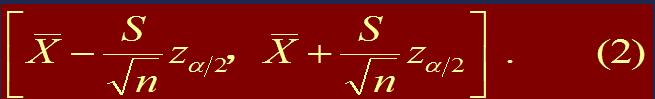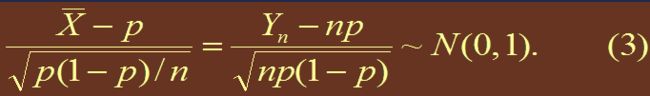高等数理统计（二）

引言

　　【比较官方的简介】数理统计学是一门以概率论为基础，应用性很强的学科。它研究怎样以有效的方式收集、 整理和分析带有随机性的数据，以便对所考察的问题作出正确的推断和预测，为采取正确的决策和行动提供依据和建议。数理统计不同于一般的资料统计，它更侧重于应用随机现象本身的规律性进行资料的收集、整理和分析。

　　【简单的讲】，就是通过样本分析来推断整体。

　　【意义或者重要性】在这个大数据时代，数据是非常重要的。怎样挖掘数据内部的规律或者隐含的信息，变得尤为重要。当时我们是不可能获得整体的数据的，所以我们只能通过抽取样本，进而通过样本来推断整体的规律。

　　【目录】

　　第一章、样本与统计量

　　　　一、引言：

　　　　二、总体与样本：

　　　　三、统计量：

　　　　四、常用分布：

　　第二章、参数估计

　　　　一、引言：

　　　　二、点估计——矩估计法：

　　　　三、点估计——极大似然估计：

　　　　四、估计量的优良性准则

　　　　五、区间估计——正态分布

　　　　　　1、引入

　　　　　　2、单个正态总体参数的区间估计

　　　　　　3、两个正态总体的区间估计

　　　　六、区间估计——非正态分布：

　　　　　　1、大样本正态近似法

　　　　　　2、二项分布

　　　　　　3、泊松分布

　　第三章、假设检验

　　　　一、引言：

　　　　二、正态总体均值的假设检验

　　　　　　1、单正态总体 N(μ, σ²)均值 μ 的检验

　　　　　　　　（1） 双边检验 H₀: μ = μ₀；H₁: μ≠μ₀ 

　　　　　　　　（2） 单边检验 H₀: μ = μ₀；H₁: μ>μ₀

　　　　　　2、两个正态总体 N(μ₁, σ₁²) 和  N(μ₂, σ₂²)均值的比较

　　　　　　　　（1） 双边检验 H₀: μ₁ = μ₂；H₁: μ₁≠μ₂ 

 　　　　　　  　（2） 单边检验 H₀: μ₁ >= μ₂；H₁: μ₁<μ₂ 

　　　　　　　　（3） 单边检验 H₀: μ₁ <= μ₂；H₁: μ₁>μ₂ 

　　　　三、正态总体方差的检验

　　　　　　1、单个正态总体方差的 χ2 检验

　　　　　　　　（1） H₀: σ² =σ₀²；H₁: σ² ≠σ₀²

　　　　　　　　（2） H₀: σ² =σ₀²；H₁: σ² >σ₀²

　　　　　　　　（3)  H₀: σ² ≤σ₀²；H₁: σ² > σ₀² (同2.)

　　　　　　2、两正态总体方差比的 F 检验

　　　　　　　　　(1).  H₀: σ₁² = σ₂²；H₁: σ₁² ≠  σ₂².

　　　　　　　　 （2） H₀: σ₁² = σ₂²；H₁:    σ₁²> σ₂²

　　　　　　　　 （3） H₀: σ₁² ≤ σ₂²；H₁:    σ₁²> σ₂²

 

第二章、参数估计

　　本讲首先介绍参数矩估计的基本思想以及求矩估计的步骤，给出多个求参数矩估计的例子；然后介绍参数极大似然估计的基本原理，求极大似然估计的基本方法，给出多个求参数极大似然矩估计的例子。

一、引言：

　　数理统计的任务： ● 总体分布类型的判断； ● 总体分布中未知参数的推断(参数估计与 假设检验)。

　　【参数估计】设总体 X 的分布函数为 F( x, θ )，其中θ 为未知参数或参数向量，现从该总体中抽样,得到样本X₁, X₂ , … , X_n .依样本对参数θ 做出估计，或估计参数 θ   的某个已知函数 g(θ ) 。这类问题称为参数估计。参数估计包括：点估计和区间估计。

　　为估计参数 µ，需要构造适当的统计量 T( X₁, X₂ , … , X_n )， 一旦当有了样本，就将样本值代入到该统计量中，算出一个值作为 µ 的估计，称该计算值为 µ 的一个点估计。

【寻求估计量的方法】

　　1. 矩估计法

　　2. 极大似然法

　　3. 最小二乘法

　　4. 贝叶斯方法 …

　　我们仅介绍前面的两种参数估计法 。

二、点估计——矩估计法

　　矩估计是基于“替换”思想建立起来的一种参数估计方法 。最早由英国统计学家 K. 皮尔逊 提出。其思想是: 用同阶、同类的样本矩来估计总体矩。

 

【步骤】

设总体 X 的分布函数中含 k 个未知参数 θ₁,θ₂,...,θ_k。

步骤一：记总体 X 的 m 阶原点矩 E(X^m)为 a_m , m  = 1,2,…,k.

一般地, a_m (m = 1, 2, …, K) 是总体分布中参数或参数向量 (θ₁,θ₂,...,θ_k) 的函数。

故, a_m (m=1, 2, …, k) 应记成: a_m(θ₁,θ₂,...,θ_k), m =1, 2, …, k.

步骤二：算出样本的 m 阶原点矩

步骤三：令

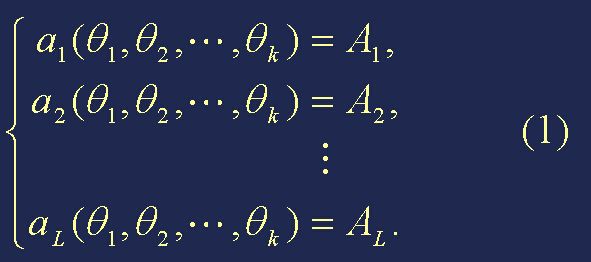  得到关于 θ₁,θ₂,...,θ_k 的方程组(L≥k)。一般要求方程组(1)中有 k 个独立方程。

步骤四：解方程组(1), 并记其解为

这种参数估计法称为参数的矩估计法，简称矩法。

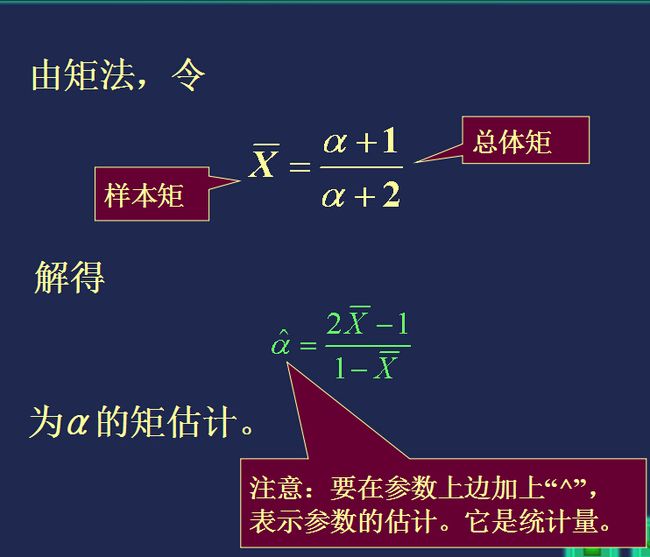
 【例题】

 

【优缺点】

矩估计的优点是：简单易行, 不需要事先知道总体是什么分布。

缺点是：当总体的分布类型已知时，未充分利用分布所提供的信息；此外，一般情形下，矩估计不具有唯一性 。

 

三、点估计——极大似然估计

　　极大似然估计法是在总体的分布类型已知前提下，使用的一种参数估计法 。该方法首先由德国数学家高斯于 1821年提出，其后英国统计学家费歇于 1922年发现了这一方法，研究了方法的一些性质，并给出了求参数极大似然估计一般方法——极大似然估计原理 。

1、极大似然估计原理

　　设总体 X 的分布 (连续型时为概率密度，离散型时为概率分布) 为 f(x, θ) ,  X₁,X₂,…,X_n 是抽自总体 X 的简单样本。于是，样本的联合概率函数 (连续型时为联合概率密度，离散型时为联合概率分布) 为

假定现在我们观测到一组样本 X₁, X₂, …,  X_n，要去估计未知参数θ 。一种直观的想法是：哪个参数(多个参数时是哪组参数) 使得现在的出现的可能性 (概率) 最大，哪个参数(或哪组参数)就作为参数的估计。这就是极大似然估计原理。

如果

， 称  为θ 的极大似然估计 (MLE)。

【极大似然估计(MLE)的一般步骤】

1、 由总体分布导出样本的联合概率函数(连 续型时为联合概率密度, 离散型时为联合 概率分布)；

2、把样本的联合概率函数中的自变量看成 已知常数, 参数θ 看成自变量, 得到似然 函数 L(θ )；

3、求似然函数 L(θ ) 的最大值点 (常常转化 为求ln L(θ )的最大值点) ，即 θ 的MLE;

4、在最大值点的表达式中，代入样本值， 就得参数 θ 的极大似然估计。

【两点说明】

●  求似然函数 L(θ ) 的最大值点，可应用微积分中的技巧。由于  ln(x)  是 x 的增函数，所以 ln L(θ ) 与 L(θ  ) 在 θ  的同一点处达到各自的最大值。假定 θ 是一实数,  ln L(θ )是 θ 的一个可微函数。通过求解似然方程

 可以得到 θ   的MLE。

● 用上述方法求参数的极大似然估计有时行不通，这时要用极大似然原理来求 。

【例题】例1: 设X₁, X₂, …, X_n是取自总体 X~B(1, p) 的一个样本，求参数 p 的极大似然估计。

 

四、估计量的优良性准则：

　　从前面两节（矩估计和极大似然）的讨论中可以看到:

　　● 同一参数可以有几种不同的估计，这时就需要判断采用哪一种估计为好的问题。

　　● 另一方面，对于同一个参数，用矩法和极大似然法即使得到的是同一个估计, 也存在衡量这个估计优劣的问题。

　　估计量的优良性准则就是：评价一个估计量“好”与“坏”的标准。

1、无偏性：

【例如】若 Θ 指的是正态总体N(μ , s²)的均值m,则其一切可能取值范围是(-∞,∞)。若 Θ 指的是方差s²，则其一切可能取值范围是(0,∞)。

 

【例题】正态分布的无偏估计

注意：E（X²） = Var （X） + [ E（X）]²    (具体详见高等数理统计（一）——> 三、统计量 ——> 1、随机变量的数字特征： ——> （2）方差)

均方误差准则

五、区间估计——正态分布:

1、引入：

　　前面讨论了参数的点估计。点估计就是利用样本计算出的值 (即实轴上点) 来估计未知参数。其优点是：可直地告诉人们  “未知参数大致是多少”；缺点是：并未反映出估计的误差范围 (精度)。故，在使用上还有不尽如人意之处。而区间估计正好弥补了点估计的这一不足之处 。

【例如】在估计正态总体均值 µ 的问题中,若根据一组实际样本，得到 µ 的极大似然估计为 10.12。实际上，µ 的真值可能大于10.12，也可能小于10.12。

　　一个可以想到的估计办法是：给出一个区间，并告诉人们该区间包含未知参数 µ 的可靠度 (也称置信系数)。

　　也就是说，给出一个区间，使我们能以一定的可靠度相信区间包含参数 µ 。

　　这里的“可靠度”是用概率来度量的，称为置信系数，常用 1- α 表示 （0 < α <1）。

　　置信系数的大小常根据实际需要来确定，通常取0.95或0.99，即 α=0.05或0.01。

   

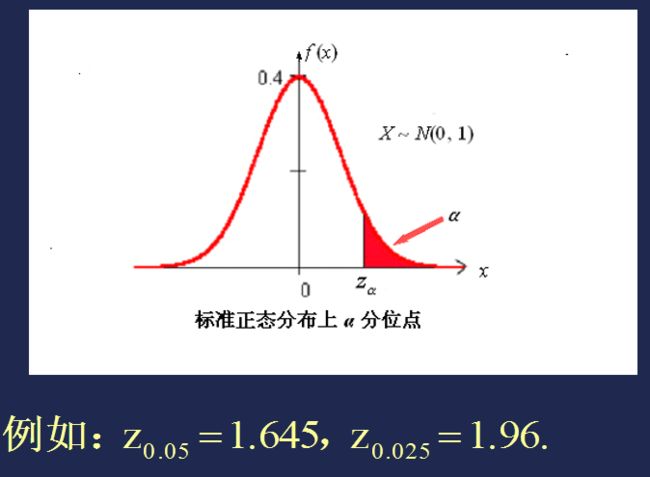
　　为确定置信区间，我们先回顾前面给出的随机变量的上α 分位点的概念。

详见第一章的【常用分布】。现在回到寻找置信区间问题上来。

【置信区间的定义】

 

2、单个正态总体参数的区间估计:

(1)σ² 已知时，对μ的区间估计：正态分布

【例1】某厂生产的零件长度 X 服从 N( μ , 0.04),现从该厂生产的零件中随机抽取6个，长度测量值如下(单位:毫米):

    14.6,  15.l,  14.9,  14.8,  15.2,  15.1.

　　求:µ 的置信系数为0.95的区间估计。 

(2)μ、σ² 未知时，对μ的区间估计：T分布

 

【例2】为估计一物体的重量μ，将其称量10次,得到重量的测量值 (单位:  千克) 如下:

10.l, 10.0, 9.8, 10.5, 9.7, l0.l, 9.9, 10.2, 10.3, 9.9.

设它们服从正态分布 N(μ , σ²)。求μ 的置信系数为0.95的置信区间。

 

(3)μ、σ² 未知时，σ² 的区间估计：卡方分布

 

【例3(续例2)】 求σ²的置信系数为0.95的置信区间。

3、两个正态总体的区间估计：

　　在实际应用中，经常会遇到两个正态总体的区间估计问题。例如：考察一项新技术对提高产品的某项质量指标的作用，将实施新技术前的产品质量指标看成正态总体 N(μ₁, σ₁²)，实施新技术后产品质量指标看成正态总体 N(μ₂, σ₂²)。于是，评价新技术的效果问题，就归结为研究两个正态总体均值之差 μ₁-μ₂ 的问题。

【定理1】设 X₁, X₂, ···, X_m是抽自正态总体X 的简单样本，X～N(μ₁, σ₁²)，样本均值与样本方差为

Y1, Y2, ···, Yn 是抽自正态总体 Y 的简单样本，Y ～N(μ₂, σ₂²)，样本均值与样本方差为

当两样本相互独立时，有：

I、σ₁²、σ₂² 已知时:

【重要】均值相消，方差累加

 

利用该定理，我们可以得到 μ₁-μ₂ 的置信系数为 1-α 的置信区间：

【例1】(比较棉花品种的优劣)：假设用甲、乙两种棉花纺出的棉纱强度分别为 X～N(μ₁, 2.18²)和Y ～N(μ₂, 1.76²)。试验者从这两种棉纱中分别抽取样本 X₁, X₂ ,…, X₂₀₀ 和 Y₁, Y₂, …, Y₁₀₀，样本均值分别为:。求 μ₁-μ₂的置信系数为 0.95 的区间估计。  

II、当σ₁²、σ₂² 未知时，但假设σ₁²=σ₂²=σ²:

证明：

利用该定理，我们可以得到 μ₁-μ₂ 的置信系数为 1-α 的置信区间：

 

六、区间估计——非正态分布：

　　1、大样本正态近似法

　　前面两节讨论了正态总体分布参数的区间估计。但是在实际应用中，我们有时不能判断手中的数据是否服从正态分布，或者有足够理由认为它们不服从正态分布。这时，只要样本大小 n 比较大，总体均值 μ 的置信区间仍可用正态总体情形的公式（如下），所不同的是：这时的置信区间是近似的。

 【证明】

　　这是求一般总体均值的一种简单有效的方法，其理论依据是中心极限定理，它要求样本大小 n 比较大。因此，这个方法称为大样本方法。

　　设总体均值为 μ,  方差为σ2 ,  X1, X2, …, Xn 为来自总体的样本。因为这些样本独立同分布的，根据中心极限定理，对充分大的 n, 下式近似成立

　　因而，近似地有

　　于是， μ 的置信系数约为1-α 的置信区间为

　　当σ²未知时，用σ²的某个估计，如 S² 来代替，（T分布，具体同【五、区间估计——正态分布】小节）得到

　　只要 n 很大，(2)式所提供的置信区间在应用上是令人满意的。

　　那么，n  究竟多大才算很大呢？

　　显然，对于相同的 n ,   (2)式所给出的置信区间的近似程度随总体分布与正态分布的接近程度而变化，因此，理论上很难给出 n 很大的一个界限。但许多应用实践表明：当 n≥30时，近似程度是可以接受的；当 n≥50时，近似程度是很好的。

　　【例1】某公司欲估计自己生产的电池寿命。现从其产品中随机抽取 50 只电池做寿命试验。这些电池寿命的平均值为 2.266  (单位：100小时)，标准差 S=1.935。求该公司生产的电池平均寿命的置信系数为 95% 的置信区间。

　　【解】查正态分布表，得 z_{α /2}= z_0.025=1.96，由公式 (2)，得电池平均寿命的置信系数为 95% 的置信区间为

　　2、二项分布：

　　设事件 A 在一次试验中发生的概率为 p， 现在做 n 次试验，以Y_n记事件 A 发生的次数,则 Y_n ~ B(n, p)。依中心极限定理，对充分大的 n，近似地有

 

　　(3)式是(1)式的特殊情形。即近似认为： Y_n ~ N ( np,np(1-p) )  ——>  Y_n = （Y_n - np ） / sqrt（ np(1-p) ）~ N ( 0,1 )

 

　　(4)式就是二项分布参数 p 的置信系数约为1-α 的置信区间。

【证明】

【例2】商品检验部门随机抽查了某公司生产的产品100件，发现其中合格产品为84件，试求该产品合格率的置信系数为0.95的置信区间。

　　解：n=100,  Y_n=84,  α =0.05,  z_α/2=1.96,  将这些结果代入到(4)式，得 p 的置信系数为0.95的近似置信区间为 [0.77, 0.91]。

【例3】在环境保护问题中,  饮水质量研究占有重要地位， 其中一项工作是检查饮用水中是否存在某种类型的微生物。假设在随机抽取的100份一定容积的水样品中有20份含有这种类型的微生物。试求同样容积的这种水含有这种微生物的概率  p 的置信系数为0.90的置信区间。

　　解：n=100,  Yn=20,  α =0.10,  zα/2=1.645,  将这些结果代入到(4)式，得 p 的置信系数为0.90的近似置信区间为 [0.134, 0.226]。

 

　　3、泊松分布  

【例4】公共汽车站在一单位时间内 (如半小时,或1小时, 或一天等) 到达的乘客数服从泊松分布 P(λ),  对不同的车站,  所不同的仅仅是参数λ  的取值不同。现对一城市某一公共汽车站进行了100个单位时间的调查。这里单位时间是20 分钟。计算得到每 20 分钟内来到该车站的乘客数平均值为 15.2 人。试求参数 λ 的置信系数为 95%的置信区间。

　　解: n=100,  α =0.05,  zα/2=1.96,     将这些结果代入到 (5) 式,  得 λ 的置信系数为0.95的近似置信区间为 [14.44, 15.96]。

转载于:https://www.cnblogs.com/mo-wang/p/4855617.html