树状数组（BIT）

知识储备——lowbit运算

众所周知，二进制有很多奇妙的应用，这里介绍其中非常经典的一个，也就是lowbit运算，即lowbit(x)=x＆(-x)。

lowbit(x)也可以理解为能整除x的最大2的幂次。

树状数组

问题引入

问题1

问题2

树状数组定义

树状数组（Binary Indexed Tree，BIT。也称Fenwick树）。它其实是一个和sum数组类似的一维的记录和的数组。只不过它存放的不是前i个整数之和，而是在i号位之前（含i号位，下同）lowbit(i)个整数之和。 如下图所示。

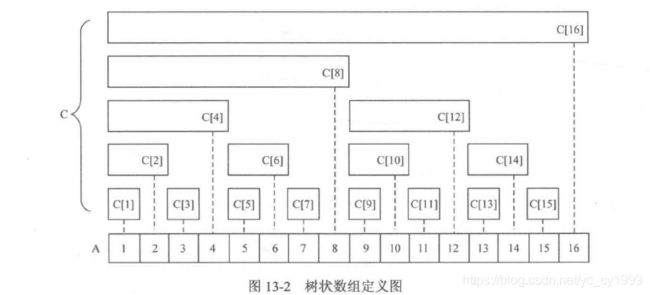
（注意，上图中的数组A和C的0号位都不存储数据~~~）
如果读者对上面的图示并未理解，那么可以继续结合下图理解：

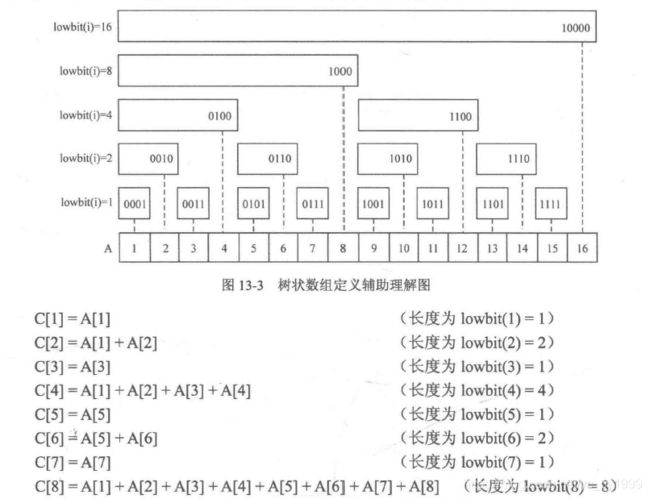
此处强调，树状数组的定义非常重要，特别是：

• C[i]的覆盖长度是lowbit(i)；
• 树状数组的下标必须从1开始；

接下来思考一下，在这样的定义下，怎样解决下面两个问题，也就是一开始提出的问题：

1. 设计函数getSum(x)，返回前x个数之和A[1]+...+A[x]。
2. 设计函数update(x,v)，实现将第x个数加上一个数v的功能，即A[x] += v;

树状数组解决方案

问题1的解决方案——getSum函数

不妨先看一个例子。
假设要查询A[1] + … + A[14]，那么从树状数组的定义出发，它实际是什么东西呢？
回到图13-2，很容易发现A[1] + … + A[14] = C[8] + C[12] + C[14]。又比如要查询A[1] + … +A[11]，从图中同样可以得到A[1] + … + A[11] = C[8] + C[10] + C[11]。那么怎么知道A[1] + … + A[x]对应的是树状数组中的哪些项呢？事实上很简单。

记SUM(1,x) = A[1] + … + A[x]，由于C[x]的覆盖长度是lowbit(x)，因此：

C(x) = A[x-lowbit(x)+1] + … + A[x]

于是马上可以得到

SUM(1,x)
= A[1] + … + A[x]
= A[1] + … + A[x-lowbit(x)] + C[x]
= sum(1,x-lowbit(x)) + C[x]

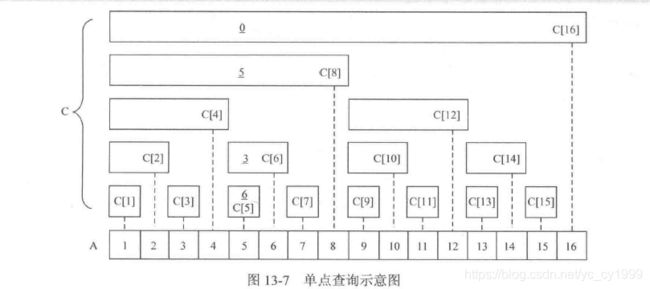
这样就把SUM(1,x)转换成SUM(1,x-lowbit(x))了，可以结合下图理解。
接下来就很容易得到getSum函数：

//getSum函数返回前x个整数之和
int getSum(int x){
	int sum = 0;	//记录和
	for(int i=x;i>0;i-=lowbit(i)){	//注意是i>0而不是i>=0 
		sum += c[i];	//累计c[i]，然后把问题缩小为SUM(1,i-lowbit(i)) 
	}
	return sum;		//返回和 
} 

显然，由于lowbit(i)的作用是：

• 定位i的二进制中最右边的1，因此i = i - lowbit(i)事实上是不断把i的二进制中最右边的1置为0的过程。

所以getSum函数的for循环执行次数为x的二进制中1的个数，也就是说，getSum函数的时间复杂度为 $O(logN)$ 。

从另一个角度理解，结合图13-2和图13-3就会发现，getSum函数的过程实际上是在沿着一条不断左上的路径进行。

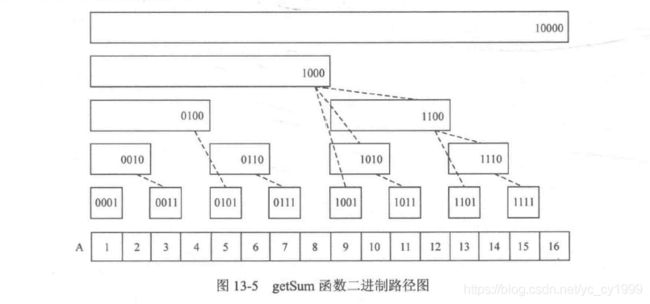
于是由于“树”高是$O(logN)$级别，因此可以同样得到getSum函数的时间复杂度就是$O(logN)$。
另外，如果要求数组下标在区间[x,y]内的数之和，即A[x] + A[x-1] + … + A[y]，可以转换成getSum(y) - getSum(x-1)来解决。

问题2解决方案——update(x,v)函数

回到图13-2，来看两个例子。假如要使A[6]加上一个数v，那么就要寻找树状数组C中覆盖了A[6]的元素，让它们都加上v。于是问题来了——想要给A[x]加上v时，怎样去寻找树状数组中的对应项呢？

首先，可以得到一个显然的结论：lowbit(y)必须大于lowbit(x)（不然怎么覆盖呢…）。

于是问题等价于求一个尽可能小的整数a，使得lowbit(x+a) > lowbit(x)。显然，由于lowbit(x)是取x的二进制最右边的1的位置，因此如果lowbit(a) < lowbit(x)，lowbit(x + a)就会小于lowbit(x)。为此lowbit(a)必须不小于lowbit(x)。于是lowbit(x+a) > lowbit(x)显然成立，最小的a就是lowbit(x)。

于是update函数的做法就很明确了，只要让x不断加上lowbit(x)，并让每步的C[x]都加上v，直到x超过给定的数据范围为止。代码如下：

//update函数将第x个整数加上v
void update(int x,int v){
	for(int i=x;i <= N; i += lowbit(i)){		//注意i必须能取到N 
		c[i] += v;		//让c[i]加上v，然后让c[i+lowbit(i)]加上v 
	} 
}

显然，这个过程是从右到左不断定位x的二进制最右边的1左边的0的过程，因此update函数的时间复杂度为$O(logN)$。

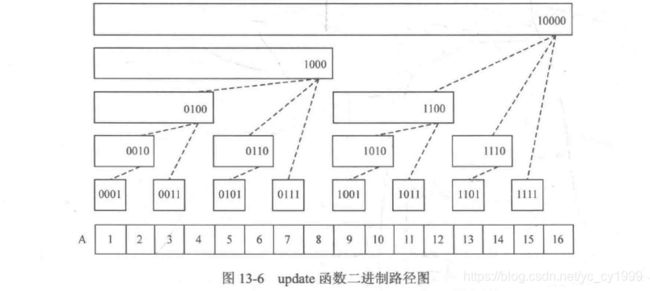
看起来update函数和getSum函数的代码相当简洁 (一个减lowbit(i)，一个加lowbit(i))，事实上它们就是树状数组的最核心的“武器”，通过它们就能解决一系列问题，接下来来看树状数组的经典应用。

树状数组应用

典型应用一

先来看使用hash数组的做法，其中hash[x]记录整数x当前出现的次数。接着，从左到右遍历序列A，假设当前访问的是A[i]，那么就令hash[A[i]]加1，表示当前整数A[i]的出现次数增加一次；同时，序列中在A[i]左边比A[i]小的个数等于hash[1]+hash[2]+ ... +hash[A[i]-1]，这个和需要输出。但是很显然，这两个工作可以通过树状数组的update(A[i],1)和getSum(A[i]-1)来解决。
使用树状数组时，不必真的建一个hash数组，因为它只存在于解法的逻辑中，并不需要真的用到，只需要一个树状数组来代替它即可。代码如下：

#include

const int maxn = 10010;

#define lowbit(i) ((i)&(-i))

int c[maxn] = {0};

void getSum(int x){
	int sum = 0;
	for(int i=x;i>0;i-=lowbit(i)){
		sum += c[i];
	}
	printf("%d",sum);
}

void update(int x,int v){
	for(int i=x;i<=maxn;i+=lowbit(i)){
		c[i] += v;
	}
}

int main(){
	int n;
	int x;
	for(int i=0;i<n;i++){
		scanf("%d",&x);
		getSum(x-1);
		update(x,1);
	}
	return 0;
} 

这就是树状数组最经典的应用，即统计序列中在元素左边比该元素小的元素个数，其中“小”的定义根据题目而定，并不一定必须是数值的大小。

那么，如何统计序列中在元素左边比该元素大的元素呢？事实上这就等价于hash[A[i]+1] +…+hash[N]，于是getSum(N) - getSum(A[i])就是答案。至于统计序列中在元素右边比该元素小（或大）的元素个数，只需要把原始数组从右往左遍历就好了。

典型应用二——离散化

#include
#include

using namespace std;

const int maxn = 10010;

#define lowbit(i) ((i)&(-i))

struct Node{
	int val;	//序列元素的值
	int pos;	//原始序号 
}temp[maxn];	//temp数组临时存放输入数据

int A[maxn];	//离散化后的原始数据 
int c[maxn]; 	//树状数组

//update函数将第x个整数加上v
void update(int x,int v){
	for(int i=x;i <= maxn; i += lowbit(i)){		//注意i必须能取到N 
		c[i] += v;		//让c[i]加上v，然后让c[i+lowbit(i)]加上v 
	} 
}

//getSum函数返回前x个整数之和
int getSum(int x){
	int sum = 0;	//记录和
	for(int i=x;i>0;i-=lowbit(i)){	//注意是i>0而不是i>=0 
		sum += c[i];	//累计c[i]，然后把问题缩小为SUM(1,i-lowbit(i)) 
	}
	return sum;		//返回和 
} 

//按val从小到大排序
bool cmp(Node a,Node b){
	return a.val<b.val;
} 

int main(){
	int n;
	scanf("%d",&n);
	
	fill(c,c+maxn,0);
	
	for(int i=0;i<n;i++){
		scanf("%d",&temp[i].val);
		temp[i].pos=i;
	}
	
	//离散化
	sort(temp,temp+n,cmp);
	
	for(int i=0;i<n;i++){
		//与上一个元素不同时，赋值为元素个数
		if(i == 0||temp[i].val != temp[i-1].val){
			A[temp[i].pos] = i+1;	//[注意]这里必须从1开始 
		}else{
			A[temp[i].pos] = A[temp[i-1].pos];
		}
	}
	//正式进入更新和求和操作
	for(int i=0;i<n;i++){
		update(A[i],1);
		printf("%d\n",getSum(A[i]-1));
	}
	return 0; 
}

一般来说，离散化只适用于离线查询，因为必须知道所有出现的元素之后才能方便进行离散化。但是对在线查询来说也不是一点办法都没有，也可以先把所有操作都记录下来，然后对其中出现的数据离散化，之后再按记录下来的操作顺序正常进行“在线”查询即可。

典型应用三——序列第K大

//求序列元素第K大
int findkthElement(int K){
	int l=1,r=MAXN,mid;		//初始区间为[1,MAXN]
	while(l<r){		//循环，直到[l,r]能锁定单一元素 
		mid = (l+r) / 2;
		if(getSum(mid) >= K) r = mid;		//所求位置不超过mid
		else l = mid + 1;		//所求位置大于mid 
	}
	return l; 
} 

注意：
在上述代码中寻找的是第一个满足条件“getSum(i)≥K”的i。（因为等于K的getSum(i)可能有多个。）

典型应用四——二维树状数组

int c[maxn][maxn];		//二维树状数组
//二维update函数位置为(x,y)的整数加上v
void update(int x,int y,int v){
	for(int i = x;i < maxn;i += lowbit(i)){
		for(int j = y;j < maxn;j += lowbit(j)){
			c[i][j] += v;
		}
	}
}

//二维getSum函数返回(1,1)到(x,y)的子矩阵中元素之和
int getSum(int x,int y){
	int sum = 0;
	for(int i = x;i > 0;i -= lowbit(i)){
		for(int j = y;j > 0;j -= lowbit(j)){
			sum += c[i][j]; 
		}
	}
	return sum;
} 

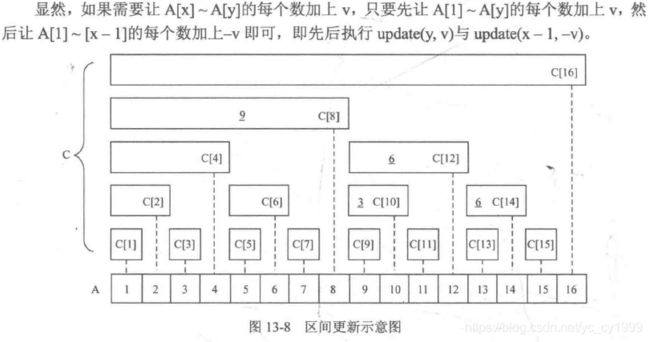
典型应用五——区间更新、单点查询

getSum(x)

//getSum函数返回第x个整数的值
int getSum(int x){
	int sum = 0;	//记录和
	for(int i = x;i < maxn;i += lowbit(i)){		//沿着i增大的路径 
		sum += c[i];	//累计c[i] 
	}
	return sum;		//返回和 
} 

update(x,v)

//update函数将前x个整数都加上v
void update(int x,int v){
	for(int i = x;i > 0;i -= lowbit(i)){	//沿着i减小的路径 
		c[i] += v;	//让c[i]加上v 
	}
}