学习笔记：机器学习--1.4正规方程求解\(\theta\)值

这是机器学习的第一章第四节：通过Normal equation(正规方程)求解\(\theta\)

在学习本节过程中，仍将提及到高等数学中矩阵的相关内容

通过这一节的学习将会了解另一种计算\(\theta\)值的方法，即Normal equation。该方法涉及到以下一个公式：

公式1.4.1：\(\theta = (X^T X)^{-1} X^T y\)

在上一节中，我们学习了Gradient descent方法循环求解\(\theta\)值，通过每一次循环逐渐逼近\(\theta\)值的最优解，从而在有限次循环后得到最终的\(\theta\)值。这一节我们介绍另外一种方法，并简要对以上两种方法进行比较。

一、Normal equation

在我们的学习中，Normal equation的核心即在于在计算机中使用公式1.4.1进行计算，对于该公式的推导，我们将不进行探讨(其中一种方法可在这里学习)。

首先我们解释公式中每一项的含义：

\(\theta\)：一个\((n+1)\times 1\)的矩阵，表示了\(\theta_0,\theta_1,\cdots,\theta_n\)共\(n+1\)个parameters，其形式如下：

\(\theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \vdots\\ \theta_n\end{bmatrix}\)

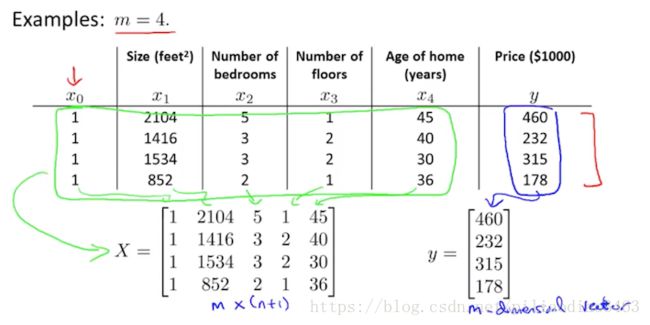
对于\(X,y\)，我们通过一个示例来进行解释，如下图所示：

\(X\)：表示所有特征的集合的矩阵，在上图示例中，即\(x^{(1)}\)到\(x^{(4)}\)的全部特征。对于共有\(m\)个training sets的情况，我们用\(x^{(i)}\)表示\(X\)如下：

\(X = \begin{bmatrix} (x^{(1)})^T\\ (x^{(2)})^T\\ \vdots\\ (x^{(m)})^T\end{bmatrix}\)

我们看到，对每一项\(x^{(i)}\)都进行了转置操作，这是因为我们定义的\(x^{(i)}\)如下：

\(x^{(i)} = \begin{bmatrix} x_0^{(i)}\\ x_1^{(i)}\\ \vdots\\ x_n^{(i)}\end{bmatrix}\)

也就是说，\(X\)是一个\((m)\times (n+1)\)矩阵，矩阵第一列是我们添加的常数\(x_0 = 1\)。

\(y\)：表示对应结果的矩阵，展开如下：

\(y^{(i)} = \begin{bmatrix} y^{(1)}\\ y^{(2)}\\ \vdots\\ y^{(m)}\end{bmatrix}\)

(在了解了每一项的含义后，我们可以通过矩阵乘法的行列关系进行一下验证：\(X\)是包含所有特征的\(m\times (n+1)\)矩阵，所以\(X^T X\)和(X^T X)^{-1}是\((n+1)\times (n+1)\)矩阵，\((X^T X)^{-1} X^T\)则是\((n+1)\times m\)矩阵，其再与矩阵\(y\)相乘后，得到\((n+1)\times 1\)矩阵。)

二、Normal equation vs Gradient descent

接下来我们对两种方法进行比较，如下图所示：

Normal equation优点：我们想到，在Gradient descent方法中，有学习速率\(\alpha\)这个东西，它定义了每次循环中\(\theta\)变化的幅度。然而在Normal equation方法中，我们没有\(\alpha\)，甚至我们可以只经过这一公式一步计算出最佳\(\theta\)矩阵。相比之下Gradient descent需要选取合适的\(\alpha\)并且需要多次循环，效率较低。

Normal equation缺点：在这一方法中，计算机按照公式计算的关键点在于计算\((X^T X)^{-1}\)这一部分，它是一个\((n+1)\times (n+1)\)矩阵。因此如果当\(n\)非常大时，计算机对其计算时就遇到了困难(计算该部分的时间复杂度为\(O(n^3)\))，其效率就有可能远远低于Gradient descent方法。(课件中给出：当达到\(n = 10^5\)左右时，就需要考虑计算机的性能，是否应该从Normal equation方法换到Gradient descent方法去了)

end~