对称加密算法总结 – 流密码与块密码
随机数
在对称加密的流密码算法和块密码算法中,都需要生成随机的密钥流,明文通过密钥加密得到密文,所以随机数生成算法显得十分重要,它决定加密密钥,密钥决定了加密算法的安全性。
随机数的类型分有三种,伪随机数生成器,密码学伪随机数生成器和真正的随机数生成器,前两者生成随机数通过软件实现,真正的随机数生成器通过硬件实现。
1、伪随机数生成器:软件实现,随机性。
2、密码学伪随机数生成器:软件实现,随机性,不可预测性。
3、真正的随机数生成器:硬件实现,随机性,不可预测性,不可重现性。
随机性很好理解,简单地说就是每个数字出现的概率是差不多的,出现的次数的平均的。不可预测性也很好理解,就是每次生成的随机数,它们之间是没有关联的,我们无法从前面生成的随机数中找到规律,从而推导出后面可能生成的随机数。不可重现性的意思就是随机数生成器不会生成完全一样的两个随机数,无论经过多长时间。
“内部状态“(internal state)
上面的三种随机数生成器,其内部生成原理都是一样的,它们都需要维护一个“内部状态“。拿伪随机数生成器举例,c语言中的rand()函数用来生成一个随机数他,它就是一个伪随机数生成器,通过算法得到随机数,对于伪随机数生成器来说,里面维护的内部状态称为”种子“,使用过rand()函数生成随机数的同学都知道,假如我们只是单纯地int a = rand();那么每次得到的随机数a都是一样的。原因是rand()函数,随机数生成器,是根据”种子“的值,结合算法公式计算出一个随机数的,这个”种子“在计算机启动后就生成了,并且值是固定的,所以根据这个固定的”种子“结合特定的算法公式,每次计算出来的随机数都是一样的。为了得到不同的随机数,使用rand()函数,每次都要重新”播种“,也就是传入不同值的”种子“,具体在这里不详述,大家可以自行查找随机数函数的用法,大多都会讲到如何重新产生”种子“。这里我们要知道,伪随机数生成器是软件层面,根据内部状态”种子“结合特定算法公式,得到的随机数。
对于硬件实现的真正的随机数生成器,它内部也维护了一个“内部状态“,之所以它能生成不可预测性,不可重现性的随机数,很重要是因为它的内部状态,称为”熵“,数值来自于外部如温度和时间等。
对称加密
数据加密算法主要有对称加密和非对称加密两种,对称加密,简单地说就是使用一个密钥加一个算法来加密明文,得到不规则的密文,加密和解密的过程是可以互逆的,明文通过密钥和算法经过计算得到密文,反过来密文通过相同的密钥和算法,可以计算得到明文,显然对称加密中加密和解密都使用的同一个密钥,密钥是一串数字,密钥的长度决定了该加密算法的安全性。
对称加密算法分两大类,流密码算法和块密码算法。
流密码算法
流密码算法,或者叫序列密码,算法大概的原理是,每次加密都通过密钥生成一个密钥流,解密也是使用同一个密钥流,明文与同样长度的密钥流进行异或运算得到密文,密文与同样的密钥流进行异或运算得到明文。流密码算法是以“一次性密码本“为雏形演变出来的加密算法,一次性密码本算法很重要的一个特性就是密钥使用的”一次性“,来看看一次性密码本的算法原理。
一次性密码本
一次性密码本的操作核心是异或运算,明文和同样长度的密钥进行异或运算,得到密文,密文根据加密时使用的的密钥进行异或运算,解密得到明文。举个例子,假如我们的明文是:
00100110 11110110 11110110 11100110
使用的加密密钥是:
10011110 10100110 11010110 11001110
那么明文与密钥进行加密异或运算,得到的密文就是:
10111000 01010000 00100000 00101000
之后密文通过同样的密钥进行异或运算,即可解密出明文:
10111000 01010000 00100000 00101000
10011110 10100110 11010110 11001110
00100110 11110110 11110110 11100110
这就是一次性密码本的原理,一次性密码本保证安全性的方法是,每一次加密解密后,下一次加密解密会更换不同的密钥,也就是每次都更换密钥。对于同一个明文信息,每一次加密都会使用不同的密钥,这样即使别人掌握了其中一个密钥和密文,他也无法确定这个密文是否是通过这个密钥加密生成的,无法确定该密文使用这个密钥解密出的就是原始明文。
流密码算法便是以一次性密码本为雏形实现的加密算法,由上面一次性密码本的原理可以看到,安全性关键在于每次都要更换密钥,这个密钥就是一次性的。流密码算法是如何实现一次性的密钥?答案就是使用随机数生成器。将密钥作为“内部状态“传入随机数生成器中,每次由随机数生成器生成随机的密钥流,然后明文和密文都使用相同的密钥流进行异或运算加密和解密。
块密码算法
块密码算法也叫分组密码算法,从字面意思就可以知道,它把加密和解密序列分成了一个个分组,最后把每一块序列合并到一起,形成明文或者密文。根据不同的分组加密方式,每个分组之间可以有联系,也可以没有联系,下面来看看块密码算法的三种模式。
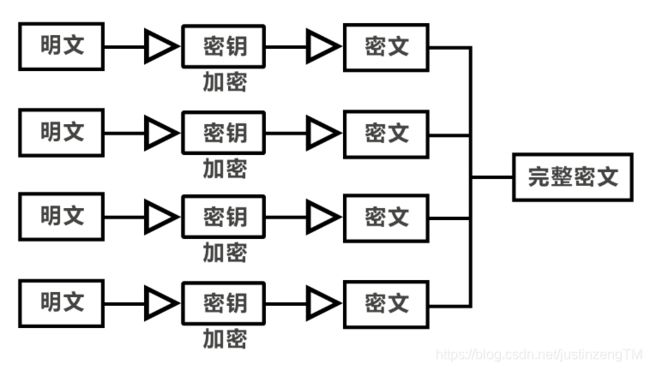
ECB电码本模式
ECB电码本模式,将明文拆分成一个一个等长字节的数据块,然后依次对每一个数据块进行密钥加密得到密文,最后将一个一个的密文分组按顺序合成一个序列,得到密文。
ECB电码本模式的优点是,每一个数据分组的加密和解密过程都可以互相独立,只需要密钥就可以进行,所以使用EBC电码本模式的加密和解密过程都可以并行处理,大大提高了处理速度。不过,这种分组之间互相独立,没有联系的加密方式,被证实是不安全的。原因是对于相同的明文,使用相同的密钥加密得到的密文是一样的,即使它们被分了组,例如一个明文序列中出现多个字符‘a’,在多个分组中都存在该字符,由于每一个分组使用的都是同一个加密密钥,所以多个分组中的字符‘a’都会被加密得到相同的密文。这样很容易被发现规律,当被发现使用的是EBC电码本模式进行加密后,破解就变得很容易了,所以该加密方式已经被证实是不安全的。
你可能会想到一个问题,如果明文序列按照某一固定字节长度等分,可是最后一块分组数据块发现无法等分,怎么办?当遇到某一数据块无法等分的情况,采取的是数据填充方式,填充标准有PKCS#7,PKCS#5,因为我没有去深入了解,所以在这里不详述,我们只要知道是采用数据填充方式将分组数据块填充到字节数据与前面的数据块等长即可。
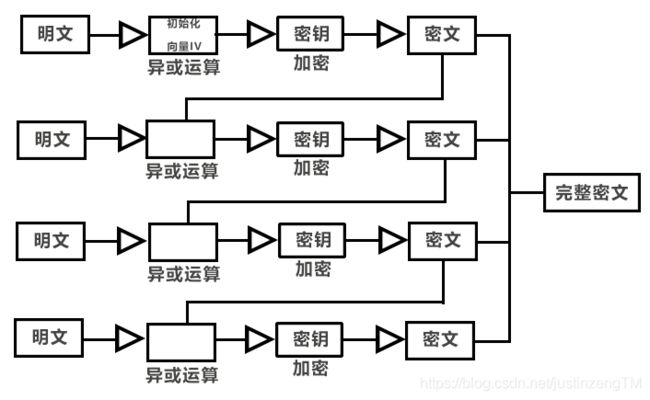
CBC密文分组连接模式
第二种是CBC密文分组连接模式,由名字可以看出,分组之间有连接,也就是分组数据块之间存在着联系,这样做可以解决EBC模式的不安全情况,看看CBC密文分组连接模式的具体过程:
- 将明文序列分成多个等长的分组数据块,如果数据块长度无法等分,那么进行填充操作。
- 依次处理每一个分组数据块,对第一个分组数据块进行加密时,利用随机数生成器生成一个初始化向量IV,数据块首先与IV进行异或运算,然后与密钥进行运算,得到第一块密文。
- 第二块分组数据块会先和前一个分组密文进行异或运算,再和密钥(使用的都是同一个密钥)进行运算得到第二块密文。也就是说,除了第一块分组数据块的初始化向量IV是通过随机数生成器生成之外,其余数据块的IV都是其前一个数据块的密文。
- 最后,将所有分组数据块密文按顺序组合成完整的密文。
可以看到CBC密文分组连接模式,通过让每一个分组之间建立联系,而不是让它们互相独立,解决了EBC电码本模式的不安全情况。第一个分组数据块的初始化向量是通过随机数生成器生成,长度和分组长度一样。明文完成加密后,将密文,初始化向量和密钥一起发送给解密人。至于解密,很简单,把步骤反过来,第一个密文与密钥运算后,和初始化向量IV进行异或运算,得到第一个明文,下一个密文分组在和密钥运算后,和前一个明文进行异或运算,得到第二个明文。
CBC模式虽然解决了EBC模式的安全问题,但是分组数据块之间的联系,使得加密和解密必须一个接一个顺序进行,无法实现并行操作,降低了处理速度。
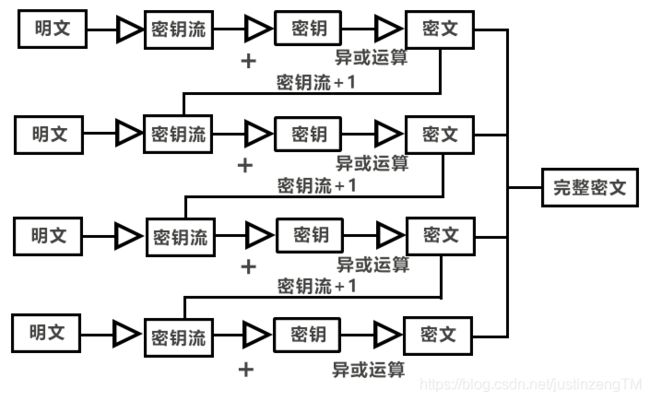
CTR计数器模式
最后一种,CTR计数器模式,它同样在每一个分组数据块之间建立联系,引入的是随机密钥流变量,类似于初始化向量。来看看具体过程更好说明它的原理:
- 第一步和前面一样还是进行分组处理,不过不需要对不等长的分组数据块进行填充处理。
- 开始依次处理每一个分组数据块,首先生成一个随机密钥流,把密钥流与密钥流进行运算后,得到的值再和明文进行异或运算,得到密文。
- 下一个密文分组,也需要先将密钥流和密钥流进行运算,这个密钥流是前一个密钥流是有联系的,可以根据一个密钥流得到下一个密钥流,最简单的方式是递增。所以第n个分组数据块的密钥流是第n-1个分组的密钥流加一。
- 得到密钥流和密钥运算后的值,第二个分组数据块就可以与该值进行异或运算,得到分组密文,然后把密钥流加一,得到下一个分组数据块的密钥流。
使用CTR计数器模式一样解决了EBC模式的安全问题,因为分组数据块之间建立了联系,就是那个密钥流,第一个随机密钥流通过随机数生成器生成,有多少个分组数据块就有多少个密钥流,每个密钥流之间有规律联系。至于拿到密文后的解密过程,比CBC模式更简单明了,先把密钥流和密钥进行运算处理后,再和密文进行异或运算,即可得到一块分组明文,最后按顺序把所有明文拼凑在一起即可。