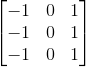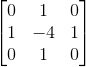实战精通OpenCV第一章--基于Android的图片卡通化及肤色改变（一）

转载请注明出处：https://blog.csdn.net/mymottoissh/article/details/86709457

本系列博客是基于《Mastering OpenCV with Practical ComputerVision Projects》

附本书电子版的下载地址：https://homepages.thm.de/~hg11237/Start/OpenCV/Mastering%20OpenCV%20with%20Practical%20Computer%20Vision%20Projects%20%5BeBook%5D.pdf

书归正传，开始正文。

第一章 基于Android的图片卡通化及肤色改变

本章将分三篇进行阐述：

一、基于Visual Studio的图片卡通化

二、基于Visual Studio的肤色改变

三、Android代码移植

本篇是第一篇

本篇涉及到的主要知识点包括：

• 实现图片卡通化的基本思路
• 双边滤波
• 边缘检测之拉普拉斯算子、Sobel算子及Scharr算子

处理流程：

上效果图

第一幅为原图，第二幅为卡通化后的图片，第三幅为黑（鬼）化的图片。

为了能从原图获得一张卡通化的图片，首先确定思路。

1. 去噪声。
2. 通过边缘检测，获取图像的轮廓作为掩膜。
3. 平坦化图片中低频部分，使其看起来更加卡通化。
4. 将2、3得到的幅图片叠加得到最终图片。

第一步去噪。选择是中值滤波滤除噪点。这个不多说了。

然后是边缘检测。关于如何选用滤波器，引用一段书中的原话：

There are many different edge detection flters, such as Sobel, Scharr, Laplacian filters, or Canny-edge detector. We will use a Laplacian edge flter since it produces edges that look most similar to hand sketches compared to Sobel or Scharr, and that are quite consistent compared to a Canny-edge detector, which produces very clean line drawings but is affected more by random noise in the camera frames and the line drawings therefore often change drastically between frames.

 简单地说选择了拉普拉斯算子。原因是，相比于其他滤波器，拉普拉斯得到的结果看起来更像素描的感觉。关于涉及到的理论知识在最后统一进行阐述。总之第二步，高斯滤波器进行边缘提取，生成一副素描图片。为了使素描更加清晰，需要对其进行二值化处理。

接下来是将平坦区域进一步柔化。这里选用双边滤波，在柔化平坦区域的同时，还能保证边缘不被模糊掉。双边的缺点是速度慢。为了加速滤波过程，这里采用了一个小技巧：首先缩小图片，然后进行双边滤波，最后复原图片。效果与直接对原图片进行滤波差不多，速度却快上几倍。

最后叠加图片。

上代码：

void cartoonifyImage(Mat& src, Mat& dst)
{
	Mat gray;
	cvtColor(src, gray, CV_BGR2GRAY);
	const int MEDIAN_BLUR_FILTER_SIZE = 7;
	medianBlur(gray, gray, MEDIAN_BLUR_FILTER_SIZE); // 中值
	Mat edges;
	const int LAPLACIAN_FILTER_SIZE = 5;
	Laplacian(gray, edges, CV_8U, LAPLACIAN_FILTER_SIZE); // 拉普拉斯
	Mat mask;
	const int EDGES_THRESHOLD = 80;
	threshold(edges, mask, EDGES_THRESHOLD, 255, THRESH_BINARY_INV); //二值化

	// 图片缩小
	Size size = src.size();
	Size smallSize;
	smallSize.width = size.width / 2;
	smallSize.height = size.height / 2;
	Mat smallImg = Mat(smallSize, CV_8UC3);
	resize(src, smallImg, smallSize, 0, 0, INTER_LINEAR);
	
    // 双边滤波
	Mat tmp = Mat(smallSize, CV_8UC3);
	int repetitions = 7;
	for (int i = 0; i < repetitions; i++)
	{
		int ksize = 9;
		double sigmaColor = 9;
		double sigmaSpace = 7;
		bilateralFilter(smallImg, tmp, ksize, sigmaColor, sigmaSpace);
		bilateralFilter(tmp, smallImg, ksize, sigmaColor, sigmaSpace);
	}

    // 图像复原
	Mat bigImg;
	resize(smallImg, bigImg, size, 0, 0, INTER_LINEAR);
	dst.setTo(0);
	bigImg.copyTo(dst, mask);
}

有了图像卡通化的基础，把人脸画成黑鬼也就不难了。需要做的就是对图片进行两次Scharr滤波，并把两次结果叠加。将最终结果叠加到原图中即可。

void evilImage(Mat& src, Mat& dst)
{
	Mat gray, mask;
	cvtColor(src, gray, CV_BGR2GRAY);
	const int MEDIAN_BLUR_FILTER_SIZE = 7;
	medianBlur(gray, gray, MEDIAN_BLUR_FILTER_SIZE);

	Mat edges, edges2;
	Scharr(gray, edges, CV_8U, 1, 0);
	Scharr(gray, edges2, CV_8U, 1, 0, -1);
	edges += edges2;
	const int EVIL_EDGE_THRESHOLD = 12;
	threshold(edges, mask, EVIL_EDGE_THRESHOLD, 255, THRESH_BINARY_INV);
	medianBlur(mask, mask, 3);
	imshow("1", mask);
	dst.setTo(0);
	src.copyTo(dst, mask);
}

这张黑鬼的图片看多了真是难受啊。

理论部分

作为本次实现的主角，这里重点讲述两个知识点：双边滤波和边缘检测。

双边滤波

大多数空域滤波器在工作过程中不可避免地会导致边缘模糊，如均值滤波、中值滤波、高斯滤波等。如何能够实现在滤除平坦区域噪声时，保留边缘的锐化程度呢？这个时候就需要用到双边滤波器了。

首先给出双边滤波的解析式：

这里不对公式进行数学推导，仅阐释其物理含义。

其中k为归一化系数，c为空域权重项，s为值域权重项，均为高斯函数形式。普通的高斯滤波器仅考虑到像素位置对最终结果的影响，在处理过程中会模糊边缘。双边滤波在此基础上引入像素强度因素。像素强度差值越大，权重越小。换句话说，双边滤波将尽可能地只考虑邻域内强度相仿的像素对最后结果的影响。以此来保证边缘的锐化程度。

结合OpenCV中的函数原型

CV_EXPORTS_W void bilateralFilter( InputArray src, OutputArray dst, int d,
                                   double sigmaColor, double sigmaSpace,
                                   int borderType = BORDER_DEFAULT )

 可以看到除了输入输出图像之外，还要指定

d：滤波尺寸， 实时应用建议不超过5，离线应用建议不超过9。否则的话会很慢。

sigmaColor、sigmaSpace：由于两个权重项都是高斯函数，sigma越大，滤波效果越明显。<10时，效果不明显，>150将会产生很强的卡通效果。

boardType：用来指定补充边缘以外的像素值的方法。

其实所谓卡通化，就是使图像色彩更加平坦。为了达到这个目的，也可以采用多次滤波的方式。正如代码里写的那样。

这里直接盗张图，展示一下多次滤波后的效果

参考资料：http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html

边缘检测

在卡通化的过程中，用到了拉普拉斯滤波，黑化的过程中用到了Scharr滤波。这两种滤波器都属于边缘检测技术。

先抛开各种滤波名称不管。首先考虑一个问题，如果让你自己检测一个图像的边缘，你会如何做？要知道这个问题的答案，首先要明确什么样的点才是边缘点。现在我们有一个像素点，通过这个点水平画一条线，如果该点左边相邻的像素点的灰度值与右边相邻的像素点的灰度值相差很大，那么这是一个水平方向上的边缘点。为了使边缘突出，应有这样的处理方法：一个像素点两侧相邻的像素点灰度差值越大，滤波后该点的灰度值越大，借以凸显边缘。如果认可了这种做法，那应该很快能够得到以下的卷积模板（以下均以水平方向为例）：

其实就是梯度越大，灰度越大。进一步考虑，像素点的水平相邻像素应该有更大的权重。于是，有了Sobel算子

再进一步，Sobel算子有什么缺点呢？在实际情况下，很多时候是由于图像的边缘不够清晰，所以才需要进行边缘的锐化。考虑一个不够清晰，灰度值渐变的边缘。一阶导数对其的响应是一个恒定值，而Sobel算子就是一阶滤波器。这意味着Sobel得到的图像边缘宽度将与渐变宽度一致。这有时是我们不想得到的结果。这也是一阶算子的缺点：滤波后的边缘较宽。

如何解决这个问题呢？答案就在二阶导数！于是拉普拉斯算子登场了。

拉普拉斯算子解决了上述问题。对于渐变边缘，仍可保证较细的边缘。但与此同时，拉普拉斯引入了另外一问题：双边缘。什么情况？为了更清晰地理解上述论述，继续盗个图。

参考资料：《数字图像处理与机器视觉》

从上图还可以看出，拉普拉斯算子与渐变边缘的起点和终点都将产生锐化效果。另外，对于散点噪声滤除效果也并不好。所以，在使用时往往会首先进行低通滤波，然后再进行边缘锐化。

好了，还剩下一个Scharr算子。是酱紫滴。

也是一阶滤波器，只不过在Sobel算子的基础上进一步增大了左右邻域的权重值。同时增大了对比度，使我们的边缘更加狂野。所以针对黑化图片的需求，Scharr更加适合。

边缘检测的另外一种经典算法是Canny检测。具体的理论知识，会放到后面的章节阐述。仅需要说明的是，对于本次实验，由于Canny算法得到的边缘太细，所以不适合实验需求，没有采用。