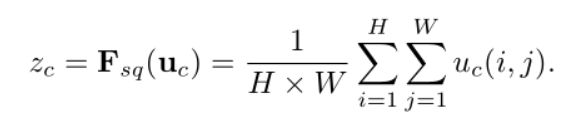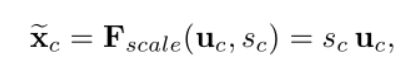- 代码练习
- 1.1 MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
- 1.2 MobileNetV2: Inverted Residuals and Linear Bottlenecks
- 1.3 HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification
- 论文阅读心得
- 2.1 Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising
- 2.2 Squeeze-and-Excitation Networks
- 2.3 Deep Supervised Cross-modal Retrieval
-
代码练习
-
1.1 MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
-
该论文的主要目的是为了构建一个能够在移动端使用的、计算量与参数量能够使得移动端接受的深度神经网络。往往还需要要求实时性能,有时候会使用某些策略来对效率与精确度进行折衷
-
该论文通过对模型的改进,大大减少了模型的参数数量和计算量,而只损失了很少的精确度,就结果来说是比较激动人心的
-
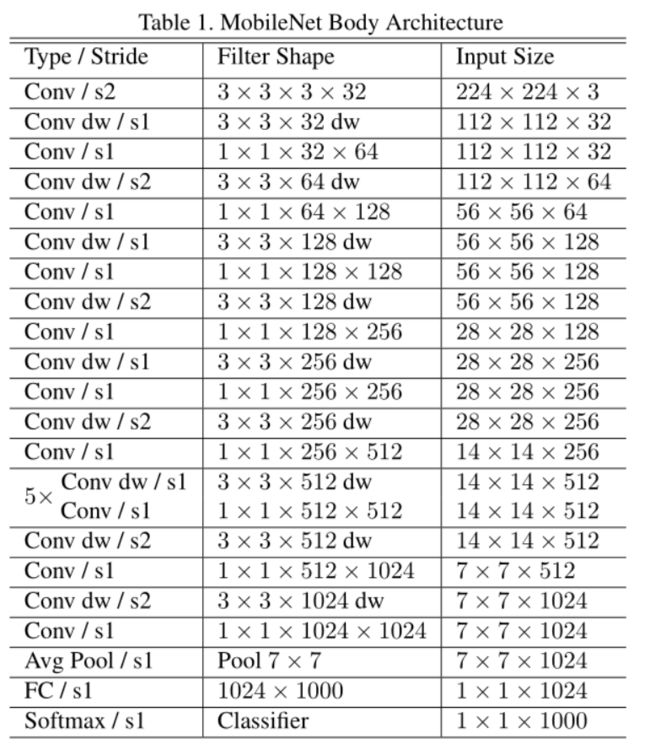
本论文中采用的模型采用了的结构来代替了传统的标准卷积结构,该结构将标准结构进行了分解。分解为了一个depthwise convolution和一个point convolution,该分解后的模型整体称为depthwise separable convolution。原始卷积为
\[G_{k,l,n}=\sum_{i,j,m}K_{i,j,m,n}·F_{k+i-1,l+j-1,m} \]depthwise convolution为
\[\hat{G}_{k,l,m}=\sum_{i,j}\hat{K}_{i,j,m}·F_{k+i-1,l+j-1,m} \]可以注意到,求和指标去掉了m,m正是表示通道数所用的,这里没有对每个通道卷积后的结果进行累加,将这种累加操作放在了point convolution层中(有关上述符号的含义,请参阅上一篇博文)
标准卷积的计算复杂度为
\[D_K·D_K·M·N·D_F·D_F \]其中\(D_K×D_K\)为卷积核大小,\(M\)为输入通道数,\(N\)为输出通道数,\(D_F×D_F\)为特征图大小
经过分解后的计算复杂模型为
\[D_K·D_K·M·D_F·D_F \]前后计算复杂度的比值仅为
\[\frac{1}{N}+\frac{1}{D_K^2} \]改进前后的结构分别为
我们可以在该表中看到模型结构为多个3×3与1×1卷积的堆叠,
-
在实现时,采用了CIFAR10数据集。对depthwise separable convolution单独块的实现如下
class Block(nn.Module): '''Depthwise conv + Pointwise conv''' def __init__(self, in_planes, out_planes, stride=1): super(Block, self).__init__() # Depthwise 卷积,3*3 的卷积核,分为 in_planes,即各层单独进行卷积 self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False) self.bn1 = nn.BatchNorm2d(in_planes) # Pointwise 卷积,1*1 的卷积核 self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False) self.bn2 = nn.BatchNorm2d(out_planes) def forward(self, x): out = F.relu(self.bn1(self.conv1(x))) out = F.relu(self.bn2(self.conv2(out))) return out -
对模型的构建如下
class MobileNetV1(nn.Module): # (128,2) means conv planes=128, stride=2 cfg = [(64,1), (128,2), (128,1), (256,2), (256,1), (512,1),(512,1),(512,1), (512,1),(512,1),(512,2), 1024,2), (1024,1)] def __init__(self, num_classes=10): super(MobileNetV1, self).__init__() self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False) self.bn1 = nn.BatchNorm2d(32) self.layers = self._make_layers(in_planes=32) self.linear = nn.Linear(1024, num_classes) def _make_layers(self, in_planes): layers = [] for x in self.cfg: out_planes = x[0] stride = x[1] layers.append(Block(in_planes, out_planes, stride)) in_planes = out_planes return nn.Sequential(*layers) def forward(self, x): out = F.relu(self.bn1(self.conv1(x))) out = self.layers(out) out = F.avg_pool2d(out, 2) out = out.view(out.size(0), -1) out = self.linear(out) return out测试结果为:
Accuracy of the network on the 10000 test images: 76.89 %
-
-
1.2 MobileNetV2: Inverted Residuals and Linear Bottlenecks
-
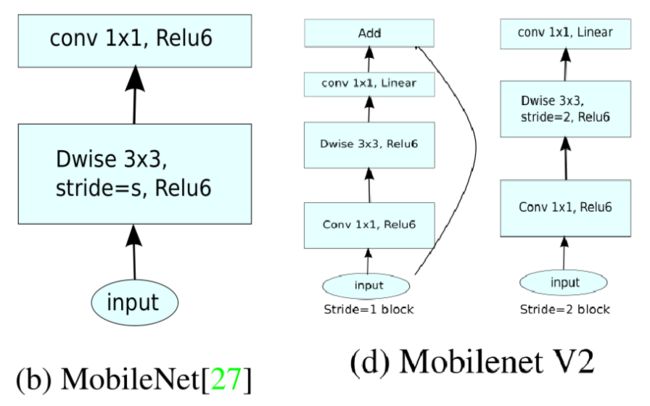
MobileNetV2增加了bottleneck的结构和残差学习的思想,论文中引入了称为inverted residual的结构,与残差结构不同的是,再输入时,引入1×1的卷积核先进行升维,然后对升维后的张量进行卷积,最后再将其降维,输入下一层
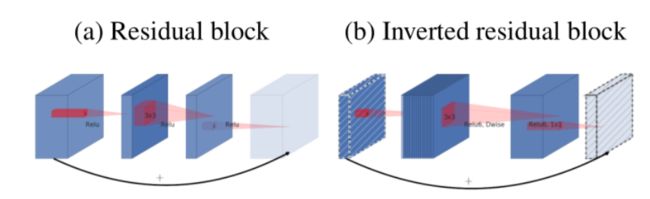
-
mobilenetv2存在两种块结构,分别是stride为1的和为2的,其结构如图
可以看到,与V1相比增加了残差结构和bottleneck结构
-
论文认为,输入模型的数据往往构成一个流形空间,该流行中的数据往往是低维流形嵌入到高维空间中形成的。如果可以在学习过程中对该流形进行抽象,去掉其他与该流形无关的多余维度的信息,保留下来纯粹的输入流形数据,那么就可以对学习模型进行简练的表示,进而促进学习效率。
-
基本块中对数据进行升维是基于一个定理。该定理表示,对一个低维流形嵌入高维空间形成的数据,在对他进行特征提取时,输入数据的维度越大,越有利于学习完整的流形信息。所以引入了先升维再降维的手段。作者给出了图片来解释这种方式的运行机制
其中input正是输入的数据,它由一个一维流形(螺旋曲线)嵌入到二维空间(曲线所在的平面)组成,而后生成一个随机的矩阵\(T\)对输入数据进行线性变换,而后经过ReLU函数,再通过\(T^{-1}\)将结果变换回去,得到之后的几张图。可以看到,当流形嵌入的高维空间维度越高时,保留的数据也就越完整。所以,使用V2中的块结构可以保留更多的输入数据的信息。
简言之,变换
\[x \approx T^{-1}ReLU(T_{m×n}x)\ \ \ \ \ \ \ \ if\ m>>n \] -
以上公式的结论即为,bottleneck结构可以避免流形数据的破坏
-
增加bottleneck的维度扩张度可以使网络表示更加复杂的函数变成可能
-
如果经过线性变换
\[D = Tx \]后,其值仍然大于0,那么如下变换即为线性变换
\[ReLU\circ T(x) \]这是由于ReLU函数对非零值的变换为恒等变换,显然为线性变换,上式即可表示为
\[R\circ T(x) \ \ \ \ \ R\ is\ linear\ transformation \]其显然也是线性变换
-
构建网络的代码如下
class MobileNetV2(nn.Module): # (expansion, out_planes, num_blocks, stride) cfg = [(1, 16, 1, 1), (6, 24, 2, 1), (6, 32, 3, 2), (6, 64, 4, 2), (6, 96, 3, 1), (6, 160, 3, 2), (6, 320, 1, 1)] def __init__(self, num_classes=10): super(MobileNetV2, self).__init__() self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False) self.bn1 = nn.BatchNorm2d(32) self.layers = self._make_layers(in_planes=32) self.conv2 = nn.Conv2d(320, 1280, kernel_size=1, stride=1, padding=0, bias=False) self.bn2 = nn.BatchNorm2d(1280) self.linear = nn.Linear(1280, num_classes) def _make_layers(self, in_planes): layers = [] for expansion, out_planes, num_blocks, stride in self.cfg: strides = [stride] + [1]*(num_blocks-1) for stride in strides: layers.append(Block(in_planes, out_planes, expansion, stride)) in_planes = out_planes return nn.Sequential(*layers) def forward(self, x): out = F.relu(self.bn1(self.conv1(x))) out = self.layers(out) out = F.relu(self.bn2(self.conv2(out))) out = F.avg_pool2d(out, 4) out = out.view(out.size(0), -1) out = self.linear(out) return out网络训练代码为
for epoch in range(10): # 重复多轮训练 for i, (inputs, labels) in enumerate(trainloader): inputs = inputs.to(device) labels = labels.to(device) # 优化器梯度归零 optimizer.zero_grad() # 正向传播 + 反向传播 + 优化 outputs = net(inputs) loss = criterion(outputs, labels) loss.backward() optimizer.step()
-
-
1.3 HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification
-
该模型的引入是为了解决高光谱图像HSI的特征提取问题,它不仅需要提取某个光谱内部的图像像素信息,还需要跨光谱进行特征提取。这方面的技术是3D卷积
-
2D卷积可以表示为
\[v_{i,j}^{x,y}=\phi(b_{i,j}+\sum_{\tau=1}^{d_{l-1}}\sum_{\rho=-\gamma}^{\gamma}\sum_{\sigma=-\delta}^{\delta}w_{i,j,\tau}^{\sigma,\rho}×v_{i-1,\tau}^{x+\sigma,y+\rho}) \]其中\(\sigma,\rho\)对\((x,y)\)点周围的像素点进行遍历以进行求和,卷积核的大小定义为\(2\gamma+1,2\delta+1\)。\(w\)为卷积核某点对应的权重。
\(\tau\) 的含义为输入图像的通道数和卷积核的层数,\(b_{i,j}\)为偏置项
这个公式还有几个点需要注意,第一点,\(i\) 应该代表的是输入层和输出层的关系,\(i-1\)应该表示的是当前所处的模型的层数(通俗的讲,也就是第几个卷积层), \(i\)指的是通过\(i-1\)层的输出作为第 \(i\) 层的输入,而后第\(i\)层应该产生什么样的输出。
这也就是论文中layer的含义。\(w\)下的 \(i\) 表示的是用第 \(i\) 层的卷积核进行计算。
第二点,应该明确输入应该是四维的,也就是
\[长×宽×通道数×特征图个数 \]这四个指标在公式中分别用 \(x,y,\tau,j\) 来表示,\(j\) 表示的应该是第几个特征图。
-
类似地,可以定义3D卷积
\[v_{i,j}^{x,y,z}=\phi(b_{i,j}+\sum_{\tau=1}^{d_{l-1}}\sum_{\lambda=-\eta}^{\eta}\sum_{\rho=-\gamma}^{\gamma}\sum_{\sigma=-\delta}^{\delta}w_{i,j,\tau}^{\sigma,\rho,\lambda}×v_{i-1,\tau}^{x+\sigma,y+\rho,z+\lambda}) \]理解了2D卷积,3D卷积仅仅是增加了一个新维度而已,\(2\eta+1\) 表征的是增加的第三个维度的卷积核的大小。在这里,第三个维度是光谱,其他应用中也可以是视频等。
-
网络模型的结构为
-
编写网络代码如下
-
-
class HybridSN(nn.Module):
def __init__(self, classes=16):
super(HybridSN,self).__init__()
self.conv3d1 = nn.Conv3d(1,8,(7,3,3))
self.conv3d2 = nn.Conv3d(8,16,(5,3,3))
self.conv3d3 = nn.Conv3d(16,32,(3,3,3))
self.conv2d1 = nn.Conv2d(576,64,(3,3))
self.relu = nn.ReLU()
self.dense1 = nn.Linear(18496,256)
self.dense2 = nn.Linear(256,128)
self.drop = nn.Dropout(p=0.4)
self.fc = nn.Linear(128,classes)
self.softmax = nn.Softmax(dim=1)
def forward(self,x):
print(x.shape)
x = self.conv3d1(x)
x = self.relu(x)
x = self.conv3d2(x)
x = self.relu(x)
x = self.conv3d3(x)
x = self.relu(x)
b,c,d,h,w = x.size()
x = x.view(b,c*d,h,w)
x = self.conv2d1(x)
x = self.relu(x)
x = x.reshape(b,-1)
x = self.dense1(x)
x = self.drop(x)
x = self.dense2(x)
x = self.drop(x)
x = self.fc(x)
return x
注意,这里最后一层不能增加softmax层,不然会造成loss震荡,造成这个的原因有可能是交叉熵函数与softmax函数冲突,通过查询资料,好像是因为交叉熵已经内置了softmax函数(待验证)
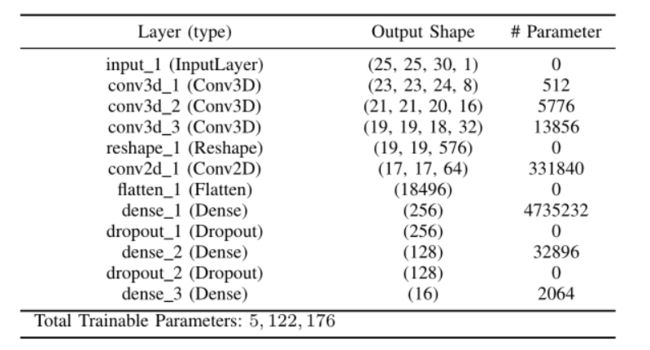
创建出来的网络结构为
torch.Size([2, 1, 30, 25, 25])
torch.Size([2, 8, 24, 23, 23])
torch.Size([2, 16, 20, 21, 21])
torch.Size([2, 32, 18, 19, 19])
torch.Size([2, 576, 19, 19])
torch.Size([2, 64, 17, 17])
torch.Size([2, 18496])
torch.Size([2, 256])
torch.Size([2, 128])
torch.Size([2, 16])
torch.Size([2, 16])
再使用一下代码对网络连通性实行测试
net = HybridSN().to(device)
from torchsummary import summary
print(summary(net,(1,30,25,25),batch_size=16))
结果为
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv3d-1 [16, 8, 24, 23, 23] 512
ReLU-2 [16, 8, 24, 23, 23] 0
Conv3d-3 [16, 16, 20, 21, 21] 5,776
ReLU-4 [16, 16, 20, 21, 21] 0
Conv3d-5 [16, 32, 18, 19, 19] 13,856
ReLU-6 [16, 32, 18, 19, 19] 0
Conv2d-7 [16, 64, 17, 17] 331,840
ReLU-8 [16, 64, 17, 17] 0
Linear-9 [16, 256] 4,735,232
Dropout-10 [16, 256] 0
Linear-11 [16, 128] 32,896
Dropout-12 [16, 128] 0
Linear-13 [16, 16] 2,064
Softmax-14 [16, 16] 0
================================================================
Total params: 5,122,176
Trainable params: 5,122,176
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 1.14
Forward/backward pass size (MB): 114.63
Params size (MB): 19.54
Estimated Total Size (MB): 135.31
----------------------------------------------------------------
-
选用交叉熵和Adam,训练模型,训练过程如下
[Epoch: 1] [loss avg: 21.5221] [current loss: 2.5986] [Epoch: 2] [loss avg: 20.3648] [current loss: 2.3049] [Epoch: 3] [loss avg: 19.6297] [current loss: 2.0657] [Epoch: 4] [loss avg: 19.0086] [current loss: 2.0880] [Epoch: 5] [loss avg: 18.3914] [current loss: 1.9932] [Epoch: 6] [loss avg: 17.7153] [current loss: 1.5524] [Epoch: 7] [loss avg: 16.8065] [current loss: 1.2607] [Epoch: 8] [loss avg: 15.8620] [current loss: 1.1177] [Epoch: 9] [loss avg: 14.9818] [current loss: 0.9448] ...... [Epoch: 91] [loss avg: 2.1086] [current loss: 0.0550] [Epoch: 92] [loss avg: 2.0868] [current loss: 0.0587] [Epoch: 93] [loss avg: 2.0652] [current loss: 0.0014] [Epoch: 94] [loss avg: 2.0440] [current loss: 0.0344] [Epoch: 95] [loss avg: 2.0242] [current loss: 0.0037] [Epoch: 96] [loss avg: 2.0055] [current loss: 0.0585] [Epoch: 97] [loss avg: 1.9879] [current loss: 0.0311] [Epoch: 98] [loss avg: 1.9724] [current loss: 0.0203] [Epoch: 99] [loss avg: 1.9555] [current loss: 0.0071] [Epoch: 100] [loss avg: 1.9382] [current loss: 0.0227] Finished Training可见已经顺利收敛
测试,结果为
precision recall f1-score support 0.0 0.7838 0.7073 0.7436 41 1.0 0.9858 0.9160 0.9496 1285 2.0 0.9752 0.9478 0.9613 747 3.0 0.9183 0.8967 0.9074 213 4.0 0.8732 0.9494 0.9097 435 5.0 0.9419 0.9878 0.9643 657 6.0 0.9130 0.8400 0.8750 25 7.0 0.9948 0.8977 0.9438 430 8.0 0.5333 0.8889 0.6667 18 9.0 0.9325 0.9794 0.9554 875 10.0 0.9654 0.9860 0.9756 2210 11.0 0.9109 0.9195 0.9152 534 12.0 0.9474 0.8757 0.9101 185 13.0 0.9734 0.9965 0.9848 1139 14.0 0.9351 0.9135 0.9242 347 15.0 0.9545 0.7500 0.8400 84 accuracy 0.9533 9225 macro avg 0.9087 0.9033 0.9017 9225 weighted avg 0.9546 0.9533 0.9532 9225准确率95%左右(学习率0.001),将学习率降低十倍,再次训练
precision recall f1-score support 0.0 0.9706 0.8049 0.8800 41 1.0 0.9836 0.9315 0.9568 1285 2.0 0.9508 0.9839 0.9671 747 3.0 0.9805 0.9437 0.9617 213 4.0 0.9772 0.9839 0.9805 435 5.0 0.9772 0.9787 0.9779 657 6.0 1.0000 0.8800 0.9362 25 7.0 0.9840 1.0000 0.9919 430 8.0 0.7778 0.7778 0.7778 18 9.0 0.9600 0.9874 0.9735 875 10.0 0.9633 0.9855 0.9743 2210 11.0 0.9542 0.9363 0.9452 534 12.0 1.0000 0.9730 0.9863 185 13.0 0.9853 0.9991 0.9922 1139 14.0 0.9908 0.9337 0.9614 347 15.0 0.9079 0.8214 0.8625 84 accuracy 0.9708 9225 macro avg 0.9602 0.9326 0.9453 9225 weighted avg 0.9710 0.9708 0.9706 9225结果稳定,准确率也有所提升,接下来将batchsize改为40,按照如上学习率继续学习
训练过程如下
[Epoch: 1] [loss avg: 66.2067] [current loss: 2.7362] [Epoch: 2] [loss avg: 63.3680] [current loss: 2.3041] [Epoch: 3] [loss avg: 58.0832] [current loss: 1.9756] ...... [Epoch: 60] [loss avg: 4.9527] [current loss: 0.0005] [Epoch: 61] [loss avg: 4.8738] [current loss: 0.0007] [Epoch: 62] [loss avg: 4.7965] [current loss: 0.0014] [Epoch: 63] [loss avg: 4.7210] [current loss: 0.0000] [Epoch: 64] [loss avg: 4.6481] [current loss: 0.0001] [Epoch: 65] [loss avg: 4.5767] [current loss: 0.0002] [Epoch: 66] [loss avg: 4.5088] [current loss: 0.0021] [Epoch: 67] [loss avg: 4.4457] [current loss: 0.0000] [Epoch: 68] [loss avg: 4.3847] [current loss: 0.0008] ...... [Epoch: 94] [loss avg: 3.2188] [current loss: 0.0001] [Epoch: 95] [loss avg: 3.1852] [current loss: 0.0001] [Epoch: 96] [loss avg: 3.1523] [current loss: 0.0003] [Epoch: 97] [loss avg: 3.1202] [current loss: 0.0008] [Epoch: 98] [loss avg: 3.0886] [current loss: 0.0032] [Epoch: 99] [loss avg: 3.0575] [current loss: 0.0009] [Epoch: 100] [loss avg: 3.0270] [current loss: 0.0003] Finished Trainingloss明显降低了,而后测试,结果如下
precision recall f1-score support 0.0 0.9512 0.9512 0.9512 41 1.0 0.9943 0.9463 0.9697 1285 2.0 0.9700 0.9946 0.9822 747 3.0 0.9767 0.9859 0.9813 213 4.0 0.9840 0.9908 0.9874 435 5.0 0.9819 0.9909 0.9864 657 6.0 1.0000 1.0000 1.0000 25 7.0 0.9954 0.9977 0.9965 430 8.0 0.9444 0.9444 0.9444 18 9.0 0.9863 0.9840 0.9851 875 10.0 0.9733 0.9882 0.9807 2210 11.0 0.9790 0.9607 0.9698 534 12.0 0.9787 0.9946 0.9866 185 13.0 0.9878 0.9947 0.9913 1139 14.0 0.9884 0.9856 0.9870 347 15.0 0.9277 0.9167 0.9222 84 accuracy 0.9816 9225 macro avg 0.9762 0.9766 0.9764 9225 weighted avg 0.9817 0.9816 0.9815 9225准确率达到了98%以上
-
论文阅读心得
-
2.1 Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising
-
2.2 Squeeze-and-Excitation Networks
-
该论文提出了一种使用权重改善输入数据不同通道注意力的机制,也就是说输入的数据由多个通道组成,作者认为这些通道对数据识别的贡献是不同的,因此作者对每个通道进行了赋权操作。使得每个通道里的特征对输出的贡献不同。
-
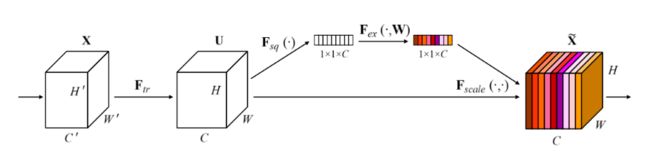
每个通道的权限是使用全剧平均池化进行计算的。
-
系统的总模型如图
图中,首先进行了一个普通卷积操作,而后对该数据进行一个权重的求解(图中上部分),而后使用求出的权重与刚才得到的数据直接加权操作,得到输出结果,可以看到输出里每一个通道具有不同的颜色,这些颜色与求出的权值一一对应
-
进行两次全连接进行池化处理的功能主要是降低计算量
-
全局平均池化的操作定义如下
-
对模型进行加权的操作如下
可以看到,加权操作只是对输入的数据简单的乘一个系数。而权重的计算(那两个全连接层的功能),也就是计算这些系数
-
-
2.3 Deep Supervised Cross-modal Retrieval
-
论文的核心是三个代价函数,分别为
\[J = J_1 + λJ_2 + ηJ_3, \\J_1 = \frac{1}{n}∥P^T U − Y∥_F + \frac{1}{n}∥P^T V − Y∥_F,\\ J_2=\frac{1}{n^2}\sum_{i,j=1}^{n}(log(1+e^{\Gamma_{ij}})-S_{ij}^{\alpha\beta}\Gamma_{ij}) \\+\frac{1}{n^2}\sum_{i,j=1}^{n}(log(1+e^{\Phi_{ij}})-S_{ij}^{\alpha\alpha}\Gamma_{ij}) \\+\frac{1}{n^2}\sum_{i,j=1}^{n}(log(1+e^{\Theta_{ij}})-S_{ij}^{\beta\beta}\Gamma_{ij}) \\J_3 = \frac{1}{n}∥U − V∥_F . \] -
有关\(J_2\)的最大似然推导为
\[-\sum_{i,j=1}^{n}(log(1+e^{\Gamma_{ij}})-S_{ij}^{\alpha\beta}\Gamma_{ij}) \\=-\sum_{i,j=1}^n{(log(1+e^{\Gamma_{ij}})-log(e^{S_{ij}^{\alpha\beta}\Gamma_{ij}}))} \\=-\sum_{i,j=1}^nlog(\frac{1+e^{\Gamma_{ij}}}{e^{S_{ij}^{\alpha\beta}\Gamma_{ij}}}) \\=\sum_{i,j=1}^nlog(\frac{e^{S_{ij}^{\alpha\beta}\Gamma_{ij}}}{1+e^{\Gamma_{ij}}}) \\=log(\prod_{i,j=1}^n\frac{(e^{\Gamma_{ij}})^{S_{ij}^{\alpha\beta}}}{1+e^{\Gamma_{ij}}}) \\=log(\prod_{i,j=1}^nf(S_{ij}^{\alpha\beta},\Gamma_{ij})) \]其中
\[f(S_{ij}^{\alpha\beta},\Gamma_{ij})=\left\{ \begin{array}{**lr**} \frac{1}{1+e^{\Gamma_{ij}}} \ \ \ \ \ \ \ if\ S_{ij}^{\alpha\beta}=0 \\\frac{e^{\Gamma_{ij}}}{1+e^{\Gamma_{ij}}} \ \ \ \ \ \ \ if\ S_{ij}^{\alpha\beta}=1 \end{array} \right. \\\delta(x)=\frac{1}{1+e^{-x}} \]\(S_{ij}^{\alpha\beta}\) 取值为0或1,两类样本本质上属于一类则为1,否则为0
所以\(J_2\)第一项显然为\(f\)的似然函数
-
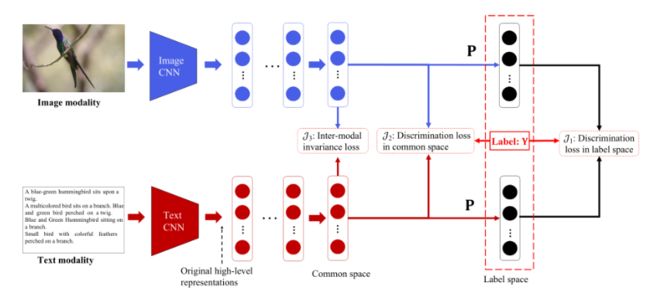
网络模型为
其中全连接层最后一层共享权重
-
算法如下
-
-
最大似然估计推导
我们定义
考虑到
我们有