题解 CF461D 【Appleman and Complicated Task】

传送门

挺难的思维题。

考虑将"x"视作1，将"o"视作0，则一个点周围四个点的异或和为0。

这样，我们得到$a_{i,j}=a_{i-1,j-1}\oplus a_{i-1,j+1}\oplus a_{i-2,j}$

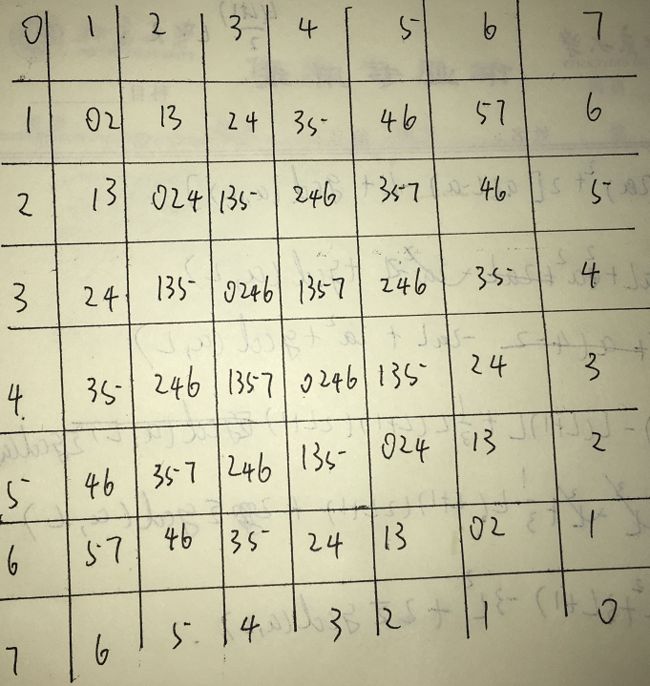
假如我们第一行已知，我们会发现这样一个东西（网上嫖的）

其中例如246的数字序列，表示这个位置的值等于第一行2，4，6位置异或起来的值

容易发现，一个点的值总是第一行某些位置的值异或起来，且这些位置同奇同偶。再分析一下，对于一个点$(i,j)$，发现它是第一行$l,l+2,...,r$异或起来的值，其中$l=abs(i+j),r=min(i+j,(n-1)\times 2-(i+j))$。（下标从0开始）

所以对第一行奇偶位置分开做异或前缀和得到$s_i$，那么对于一个给出的信息$(i,j,t)$，可以转化成第一行$s[l]\oplus s[r+2]=t$（$l-2$和$r$也是可以的，不过$l-2$会变成负数不好处理），即这两个数是否相等。然后就很套路了，拆点，用并查集判断即可。

$Codebelow:$

#include
#define ts cout<<"ok"<
#define int long long
#define hh puts("")
#define pc putchar
#define mo 1000000007
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
using namespace std;
const int N=200005;
int n,k,f[N];
char s[5];
inline int read(){
    int ret=0,ff=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') ff=-1;ch=getchar();}
    while(isdigit(ch)){ret=ret*10+(ch^48);ch=getchar();}
    return ret*ff;
}
void write(int x){if(x<0){x=-x,pc('-');}if(x>9) write(x/10);pc(x%10+48);}
void writeln(int x){write(x),hh;}
void writesp(int x){write(x),pc(' ');}
int ksm(int x,int y){
    int res=1;
    while(y){
        if(y&1) res=res*x%mo;
        y>>=1;
        x=x*x%mo;
    }
    return res;
}
int find(int x){
    return f[x]==-1?x:f[x]=find(f[x]);
}
bool merge(int x,int y){
    int tx=find(x),ty=find(y);
    if(find(x^1)==ty) return 0;
    if(find(y^1)==tx) return 0;
    if(tx!=ty) f[tx]=ty;
    return 1;
}
bool check(int l,int r,int t){
    if(t==0){//s[l]^s[r]=0
        return merge(l*2,r*2)&&merge(l*2+1,r*2+1);
    }
    else{//s[l]^s[r]=1
        return merge(l*2,r*2+1)&&merge(l*2+1,r*2);
    }
}
signed main(){
    n=read(),k=read();
    memset(f,-1,sizeof(f));
    for(int i=1;i<=k;i++){
        int x=read()-1,y=read()-1;
        int l=x-y,r=x+y;
        if(l<0) l=-l;
        if(r>n-1) r=(n-1)*2-r;
        scanf("%s",s);
        if(!check(l,r+2,s[0]=='x'?0:1)){
            write(0);
            return 0;
        }
    }
    int ans=0;
    for(int i=0;i<=(n+2)*2;i++)
        if(find(i)==i)
            ans++;
    write(ksm(2,ans/2-2));
    return 0;
}