LeetCode 34 解数独python
题目 : 编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
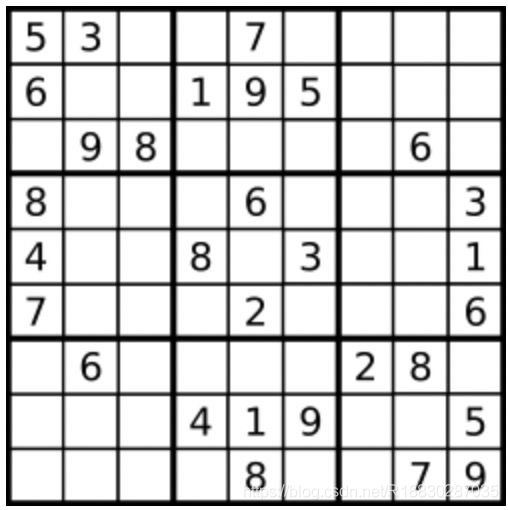
一个数独。
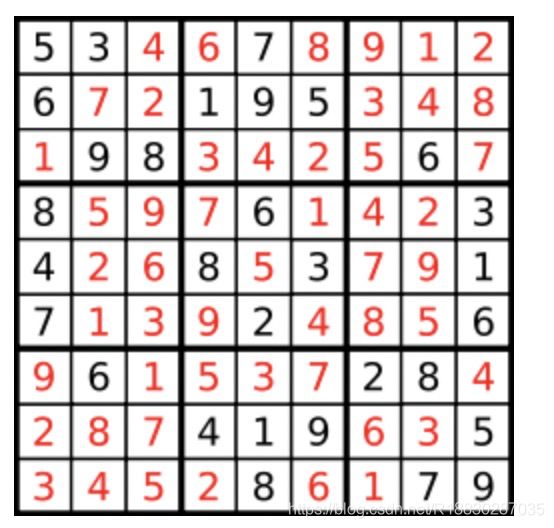
答案被标成红色。
①首先,某个方格内放入的元素,必须未出现在行,列以及对应的子区域中.所以,行,列及子区域未出现元素的交集即为该方格有可能填入的元素.如果该交集只有1个元素,那么该方格只能填入这个元素.这是第一个切入点. 所以第一个函数里下面这部分就是在求行,列及子区域可能出现的元素值.
第二个函数fill_one_hole就是前面所说的,如果某个方格内只能填入一个元素,那么就将元素填入方格中.并把对应行,列,子区域中的对应元素删掉. 随着数独区域中的数据越来越多,某些方格中可以填入的元素就越来越少,个数并逐渐趋近于1.所以如果运气比较好的话,运行这个fill_one_hole 5-10次,就可以正确填完整个数独.测试例子就能够用这个方法填完. 当然在大部分情况下,填完这些只能填1个元素的方格,剩下的方格都有大于等于2个元素可以填入.这个时候就需要使用递归和追溯了.
②递归部分.首先使用之前算出来的行,列及子区域可能出现的元素计算交集,交集中的元素就是某个方格内可能填入的元素. (我之前还额外写了一个函数来判断新填入的元素是否在行,列或子区域中出现过,现在想想有点傻了,这三者可能出现的元素取交集,那么就已经证明该元素不会和之前已经出现的元素重复了.) 首先在方格内填入一个值,如果填入的数后的数独可以继续填入数直到完成.则返回True,否则说明刚才的数填错了,再把该方格还原成’.’,并尝试下一个值. 这个过程就是用 for item in union 进行实现的. 如果所有的值都试过数独仍然解不出来,说明上一个空格的值填错了,那么直接返回False. 道路千万条,正确只一条. 可以想象得出,在一个树状的结构中,只有一条路是完全正确的,其他路都在行进过程中返回了False. 那么这条正确的路返回True即可.
注: 第二个函数fill_one_hole并不是必须的.即使不调用这个函数也能成功解出数独.但是使用这个函数能够对只能填入一个元素的方格进行特殊处理,而不是使用递归一次一次进行尝试,在一定程度上能够简化操作.
dp_row = [set([str(j) for j in range(1,10)]) for i in range(9)]
dp_column = [set([str(j) for j in range(1,10)]) for i in range(9)]
dp_area = [set([str(j) for j in range(1,10)]) for i in range(9)]
number_set = set([str(i) for i in range(1,10)])
for i in range(9):
for j in range(9):
n = (i//3)*3 + j//3
if board[i][j] != '.':
dp_row[i].remove(board[i][j])
dp_column[j].remove(board[i][j])
dp_area[n].remove(board[i][j])
for i in range(30):
self.fill_one_hole(board,dp_row,dp_column,dp_area)
self.DFS(board,dp_row,dp_column,dp_area)
def fill_one_hole(self,board,dp_row,dp_column,dp_area):
for i in range(9):
for j in range(9):
n = (i//3)*3 + j//3
union = dp_row[i] & dp_column[j] & dp_area[n]
if board[i][j] == '.' and len(union)==1:
item = union.pop()
board[i][j] = item
dp_row[i].remove(item)
dp_column[j].remove(item)
dp_area[n].remove(item)
def DFS(self,board,dp_row,dp_column,dp_area):
for i in range(9):
for j in range(9):
n = (i//3)*3 + j//3
union = dp_row[i] & dp_column[j] & dp_area[n]
if board[i][j] == '.':
for item in union:
board[i][j] = item
dp_row[i].remove(item)
dp_column[j].remove(item)
dp_area[n].remove(item)
if self.DFS(board,dp_row,dp_column,dp_area):
return True
board[i][j] = '.'
dp_row[i].add(item)
dp_column[j].add(item)
dp_area[n].add(item)
return False
return True
第二种
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
# 把所有没填数字的位置找到
all_points = []
for i in range(9):
for j in range(9):
if board[i][j] == ".":
all_points.append([i, j])
# check函数是为了检查是否在point位置k是合适的
def check(point, k):
row_i = point[0]
col_j = point[1]
for i in range(9):
# 检查 行
if i != row_i and board[i][col_j] == k:
return False
# 检查 列
if i != col_j and board[row_i][i] == k:
return False
# 检查块
for i in range(row_i//3*3 , row_i//3*3+3):
for j in range(col_j//3*3, col_j//3*3+3):
if i != row_i and j != col_j and board[i][j] == k:
return False
return True
def backtrack(i):
# 回溯终止条件
if i == len(all_points):
return True
for j in range(1, 10):
# 检查是否合适
if check(all_points[i],str(j)):
# 合适就把位置改过来
board[all_points[i][0]][all_points[i][1]] = str(j)
if backtrack(i+1): # 回溯下一个点
return True
board[all_points[i][0]][all_points[i][1]] = "."# 不成功把原来改回来
return False
backtrack(0)