D. PolandBall and Polygon----线段树（树状数组）

D. PolandBall and Polygon

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

PolandBall has such a convex polygon with n veritces that no three of its diagonals intersect at the same point. PolandBall decided to improve it and draw some red segments.

He chose a number k such that gcd(n, k) = 1. Vertices of the polygon are numbered from 1 to n in a clockwise way. PolandBall repeats the following process n times, starting from the vertex 1:

Assume you've ended last operation in vertex x (consider x = 1 if it is the first operation). Draw a new segment from vertex x to k-th next vertex in clockwise direction. This is a vertex x + k or x + k - n depending on which of these is a valid index of polygon's vertex.

Your task is to calculate number of polygon's sections after each drawing. A section is a clear area inside the polygon bounded with drawn diagonals or the polygon's sides.

Input

There are only two numbers in the input: n and k (5 ≤ n ≤ 106, 2 ≤ k ≤ n - 2, gcd(n, k) = 1).

Output

You should print n values separated by spaces. The i-th value should represent number of polygon's sections after drawing first i lines.

Examples

input

5 2

output

2 3 5 8 11 

input

10 3

output

2 3 4 6 9 12 16 21 26 31 

Note

The greatest common divisor (gcd) of two integers a and b is the largest positive integer that divides both a and b without a remainder.

For the first sample testcase, you should output "2 3 5 8 11". Pictures below correspond to situations after drawing lines.

题目链接：http://codeforces.com/contest/755/problem/D

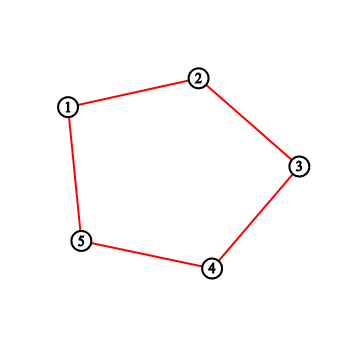
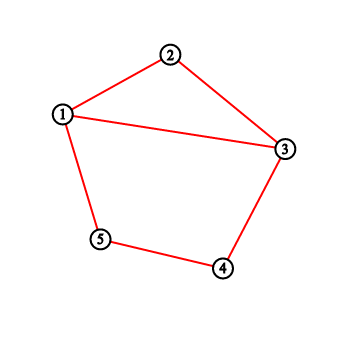
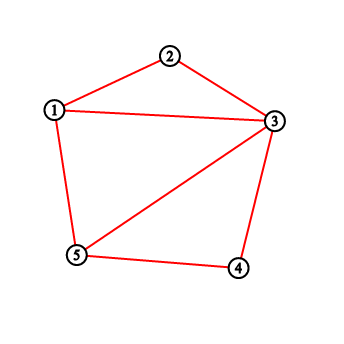
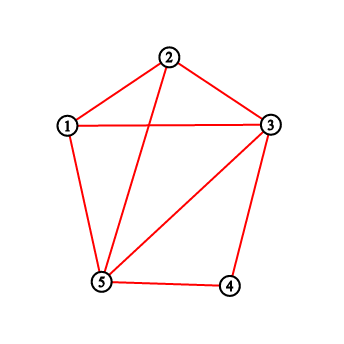
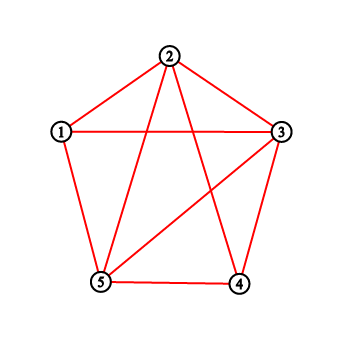
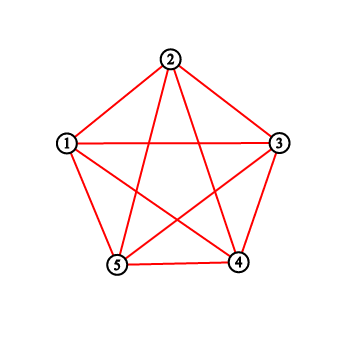
一开始这个题我找了个规律，结果错了......

题意：给出一个n边形，和距离k，第一次链接1和k+1，第二次链接k+1和（k+1+k）%n，依次进行，每次结束后输出n边形被分割成了几个区域。

有一个公式，我当时推出来了。

新加入一条直线后的区域块数 = 原有的区域块数 + 与该直线相交直线的条数 +1

很容易就能想到这个式子，但是我却没有想到用线段树或者是树状数组，太菜了。。。

有一个坑点，也是Hack点，当k>n/2时，k=n-k；

附上大牛的链接：

http://blog.csdn.net/harlow_cheng/article/details/54570832

代码：

#include 
#include 
#include 
#define LL long long
using namespace std;
const int MAXN=1e6+100;
LL sum[MAXN<<2];
int n,k;
LL query(int L,int R,int l,int r,int rt){
    if(L>R){
        return 0;
    }
    if(L<=l&&r<=R){
        return sum[rt];
    }
    int m=(l+r)>>1;
    LL ans1=0,ans2=0;
    if(L<=m){
        ans1=query(L,R,l,m,rt<<1);
    }
    if(m>1;
    if(pos<=m)
        updata(pos,l,m,rt<<1);
    else
        updata(pos,m+1,r,rt<<1|1);
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
int main(){
    scanf("%d%d",&n,&k);
    k=min(k,n-k);
    int now=1;
    LL ans=1;
    for(int i=1;i<=n;i++){
        int nex=now+k;
        LL temp;
        if(nex>n)
            temp=query(now+1,n,1,n,1)+query(1,nex-n-1,1,n,1);
        else
            temp=query(now+1,nex-1,1,n,1);
        ans+=temp+1;
        cout<n)
            nex-=n;
        updata(nex,1,n,1);
        now=nex;
    }
    return 0;
}