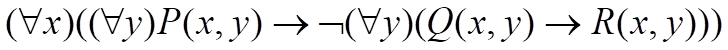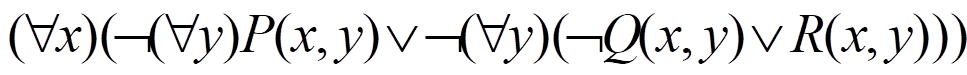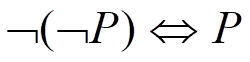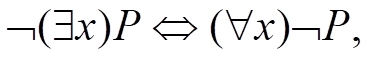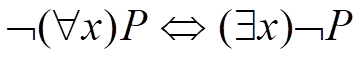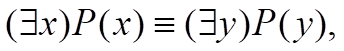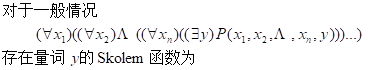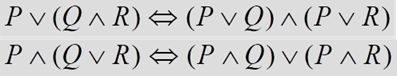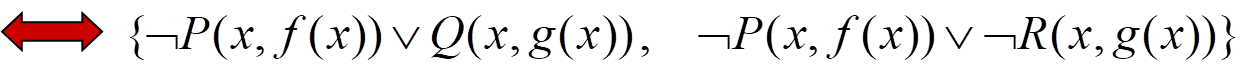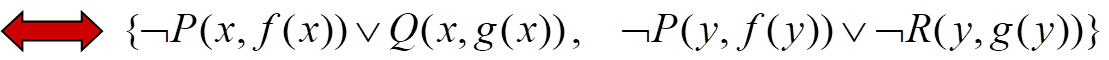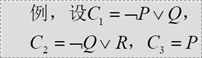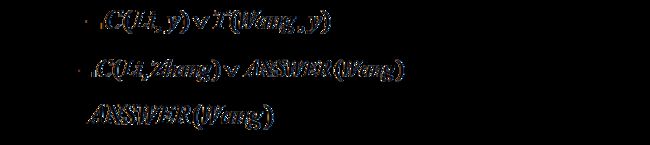人工智能 3.确定性推理方法
推理是求解问题的一种重要方法
鲁宾逊归结原理使定理证明能够在计算机上实现
知识+推理=智能
归结演绎:谓词公式化为子句集、鲁宾逊归结原理、归结反演
推理的基本概念
已知事实(数据库)+知识 --通过策略à结论
推理方式及其分类:演绎推理、归纳推理、默认推理
1.演绎推理 (deductive reasoning) : 一般 → 个别
三段论式(三段论法)
足球运动员的身体都是强壮的 ;(大前提)
高波是一名足球运动员;(小前提)
所以,高波的身体是强壮的。(结论)
2.归纳推理 (inductive reasoning): 个别 → 一般
完全归纳推理(必然性推理)(普查)、不完全归纳推理(非必然性推理)(抽样)
3.默认推理(default reasoning,缺省推理)
知识不完全的情况下假设某些条件已经具备所进行的推理。
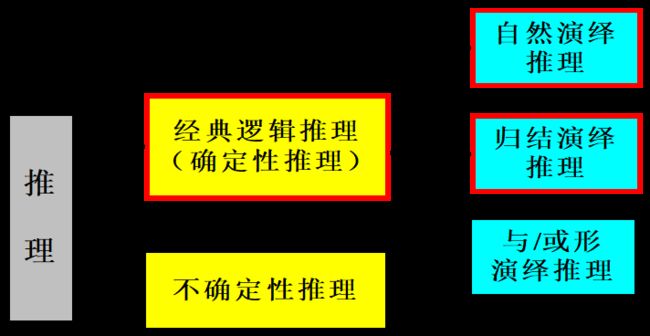
确定性推理、不确定性推理
(1)确定性推理:推理时所用的知识与证据都是确定的,推出的结论也是确定的,其真值或者为真或者为假。
(2)不确定性推理:推理时所用的知识与证据不都是确定的,推出的结论也是不确定的。
单调推理、非单调推理
(1)单调推理:随着推理向前推进及新知识的加入,推出的结论越来越接近最终目标。 (经典逻辑)
(2)非单调推理:由于新知识的加入,不仅没有加强已推出的结论,反而要否定它,使推理退回到前面的某一步,重新开始。(默认推理)
启发式推理、非启发式推理
启发性知识:与问题有关且能加快推理过程、提高搜索效率的知识。
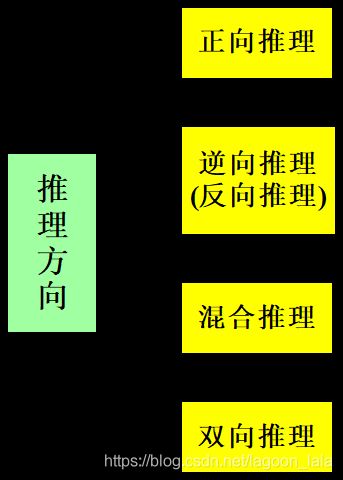
推理方向:
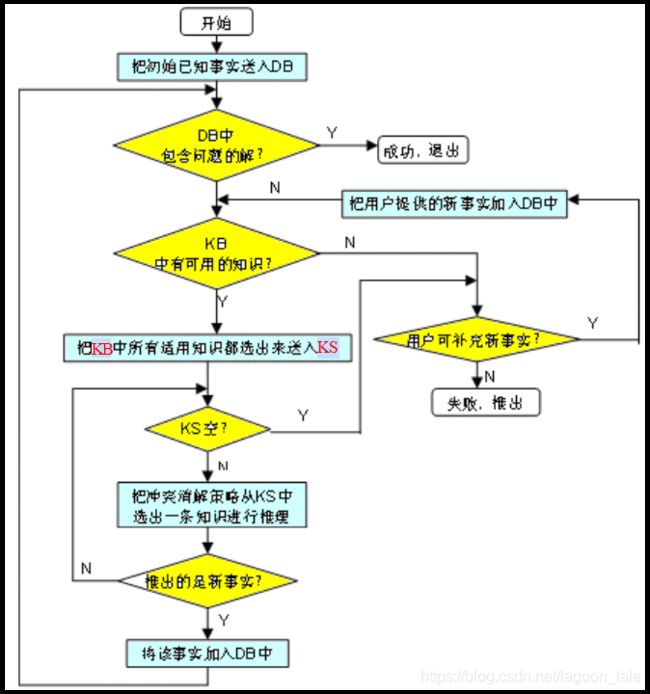
1. 正向推理(事实驱动推理): 已知事实 → 结论
(1)从初始已知事实出发,在知识库KB中找出当前可适用的知识,构成可适用知识集KS。
(2)按某种冲突消解策略从KS中选出一条知识进行推理,并将推出的新事实加入到数据库DB中作为下一步推理的已知事实,再在KB中选取可适用知识构成KS 。
(3)重复(2),直到求得问题的解或KB中再无可适用的知识。
实现正向推理需要解决的问题:
确定匹配(知识与已知事实)的方法。
按什么策略搜索知识库。
冲突消解策略。
正向推理简单,易实现,但目的性不强,效率低。
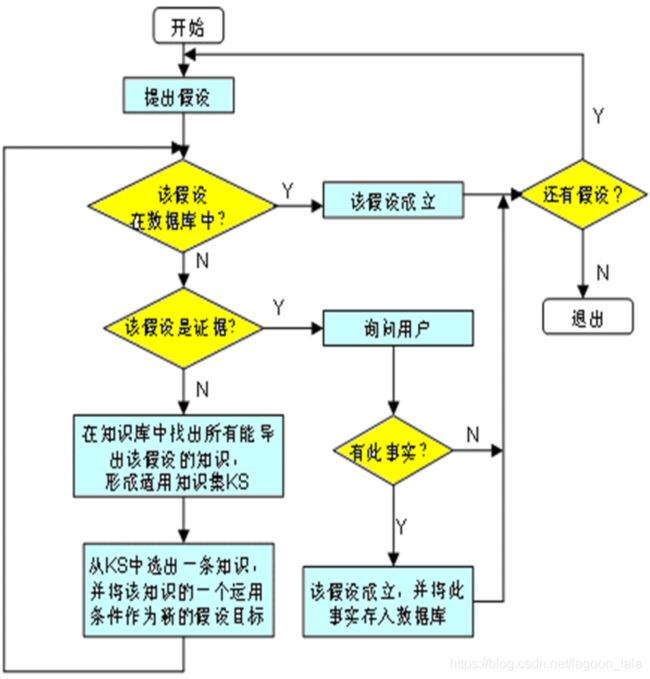
2.逆向推理(目标驱动推理):以某个假设目标作为出发点。
基本思想:
选定一个假设目标。
寻找支持该假设的证据,若所需的证据都能找到,则原假设成立;若无论如何都找不到所需要的证据,说明原假设不成立的;为此需要另作新的假设。
主要优点:不必使用与目标无关的知识,目的性强,同时它还有利于向用户提供解释。
主要缺点:起始目标的选择有盲目性。
正向推理: 盲目、效率低。
逆向推理: 若提出的假设目标不符合实际,会降低效率。
3.正反向混合推理:
(1)先正向后逆向:先进行正向推理,帮助选择某个目标,即从已知事实演绎出部分结果,然后再用逆向推理证实该目标或提高其可信度;
(2)先逆向后正向:先假设一个目标进行逆向推理,然后再利用逆向推理中得到的信息进行正向推理,以推出更多的结论。
如下为先正后逆:
4. 双向推理:正向推理与逆向推理同时进行,且在推理过程中的某一步骤上“碰头”的一种推理。
冲突消解策略:
已知事实与知识的三种匹配情况:
(1)恰好匹配成功(一对一);
(2)不能匹配成功;
(3)多种匹配成功(一对多、多对一、多对多)à需要冲突消解
多种冲突消解策略:
(1)按针对性排序
(2)按已知事实的新鲜性排序
(3)按匹配度排序
(4)按条件个数排序(少的更接近充要)
自然演绎推理
自然演绎推理:从一组已知为真的事实出发,运用经典逻辑的推理规则推出结论的过程。
推理规则:P规则(前提引入)、T规则(结论引用)、假言推理(P, P→Q=>Q)、拒取式推理(P→Q,﹁Q=>﹁P)
证明:
定义谓词:
EASY ( x ):x 是容易的
LIKE ( x, y ):x 喜欢 y
C ( x ):x 是 C 班的一门课程
已知事实和结论用谓词公式表示:
(∀x) ( EASY ( x ) → LIKE ( Wang, x ) )
(∀x) ( C ( x ) → EASY ( x ))
C ( ds )
LIKE ( Wang, ds )
(∀x)(EASY ( x ) →LIKE ( Wang, x ))
EASY (z) →LIKE ( Wang, z ) 全称固化
(∀x) (C ( x ) → EASY ( x ))
C ( y ) →EASY ( y ) 全称固化
所以 C (ds), C (y) →EASY (y) =>EASY (ds) P规则及假言推理
所以 EASY (ds), EASY (z) →LIKE (Wang,z) =>LIKE ( Wang, ds ) T规则及假言推理
缺点:易产生组合爆炸,得到的中间结论一般呈指数形式递增。
谓词公式化为子句集的方法
原子(atom)谓词公式: 一个不能再分解的命题。
文字(literal):原子谓词公式及其否定。p:正文字,﹁p:负文字。
子句(clause):任何文字的析取式。任何文字本身。
空子句(NIL):不包含任何文字的子句。永假
子句集:由子句构成的集合。
将下列谓词公式化为子句集
1)消去谓词公式中的“à”和“<-->”符号
(2)把﹁移到紧靠谓词的位置上
(3)变量标准化(辖域不同,变量名不同)
(4)消去存在量词
a. 存在量词不出现在全称量词的辖域内。
b. 存在量词出现在一个或者多个全称量词的辖域内。
![]()
(5)化为前束形
前束形=(前缀){母式}
(前缀):全称量词串。
{母式}:不含量词的谓词公式。
(6)化为 Skolem 标准形
![]()
(7)略去全称量词
(8)消去合取词
(9)子句变量标准化
谓词公式不可满足的充要条件是其子句集不可满足
鲁宾逊归结原理
子句集中子句之间是合取关系,只要有一个子句不可满足, 则子句集就不可满足。
鲁宾逊归结原理(消解原理)的基本思想:
在 S 中选择合适的子句进行归结,一旦归结出空子句,就说明 S 是不可满足的。
1. 命题逻辑中的归结原理(基子句的归结)
定义3.1(归结):设C1与C2是子句集中的任意两个子句,如果 C1中的文字L1与 C2中的文字L2互补,那么从C1和 C2中分别消去L1和L2,并将二个子句中余下的部分析取,构成一个新子句C12 。
定义:归结式C12是其亲本子句C1与C2的逻辑结论。即如果 C1与C2为真,则C12为真。
推论:设C1与C2是子句集S中的两个子句,C12是它们的归结式,若C12 加入原子句集S,得到新子句集S1,则S与S1在不可满足的意义上是等价的
S永假<=>S1永假
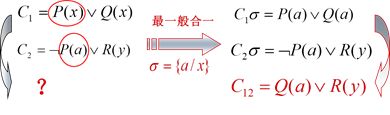
谓词逻辑中的归结原理(含有变量的子句的归结):
为C1、C2的二元归结式。
对于谓词逻辑,归结式是其亲本子句的逻辑结论。
对于一阶谓词逻辑,子句集是不可满足的ó存在一个从该子句集到空子句的归结演绎
如果没有归结出空子句,则既不能说 S 不可满足,也不能说 S 是可满足的。(可能是归结方式错了)
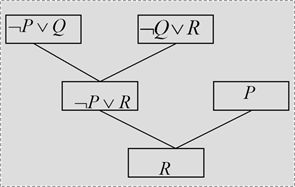
归结反演
应用归结原理证明定理的过程称为归结反演。
用归结反演证明的步骤是:
(1)将已知前提表示为谓词公式F。
(2)将待证明的结论表示为谓词公式Q,并否定得到﹁ Q 。
(3)把谓词公式集{F,﹁Q} 化为子句集S。
(4)应用归结原理对子句集S中的子句进行归结,并把每次归结得到的归结式都并入到S中。如此反复进行,若出现了空子句(P∨﹁P),则停止归结,此时就证明了Q为真。
应用归结原理求解问题
应用归结原理求解问题的步骤:
(1)已知前提 F 用谓词公式表示,并化为子句集 S ;
(2)把待求解的问题 Q 用谓词公式表示,并否定 Q,再与 ANSWER 构成析取式(﹁ Q ∨ ANSWER );(也就是QàANSWER)
(3)把(﹁ Q∨ ANSWER) 化为子句集,并入到子句集 S中,得到子句集S’;
(4)对S’应用归结原理进行归结;
(5)若得到归结式 ANSWER ,则答案就在 ANSWER 中。
已知:
:王(Wang)先生是小李(Li)的老师。
:小李与小张(Zhang)是同班同学。
:如果x与y是同班同学,则x的老师也是y的老师。
求:小张的老师是谁?
解:
定义谓词:
把已知前提表示成谓词公式:
把目标表示成谓词公式,谁教张T(x,Zhang),并把它否定后与 ANSWER 析取:
把上述公式化为子句集:
归结: