带权并查集之区间统计类和种类并查集

我们都知道普通并查集可以理解为查看集合间的关系和集合间的合并。
带权并查集不仅记录集合间关系，还记录集合内元素间的关系（元素间连线的权值）。带权并查集主要分为两类：区间统计类和种类并查集

---

一.区间统计类

例题.hdu 3038 How Many Answers Are Wrong

http://acm.hdu.edu.cn/showproblem.php?pid=3038
题意：
给你一系列区间和，判断给出的区间和中有几个是不合法的。

题解：
1.如何建立区间之间的联系
2.如何发现悖论

1.如何建立联系

首先理解字母含义：
1.fx是x的祖先，fy是y的祖先，val[x]表示x到祖先的区间和（即[fx, x]）,val[y]表示y到祖先的区间和（即[fy, y]）,w表示y到x的区间和（即[x, y]）。

重点来了，我们需要将所有区间和都视为向量，通过向量加减来判断是否存在悖论

然后分类讨论
1.fx == fy

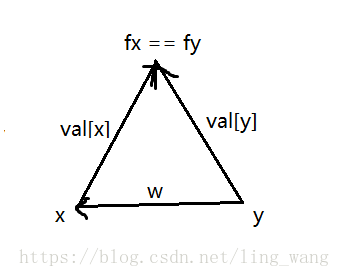
[x，y]之间的和是可以求出的。 区间[x，y]的和就是可以写成val[x] - val[y]。判断给出的w与向量法计算的区间和是否相等就可以判断是否是悖论。
2.fx ！= fy

建立新的区间关系，val[fy]表示两个区间间（val[y]和val[x]）的权值差（即fy与fx的区间和[fx,fy]）。首先将fy指向fx，这代表fx是区间的左端点;fy->fx = fy->y +y->x + x->fx;因此val[fy] = val[x] - val[y] + w

重点讲完了~
接下来就是一些细节了，比如在更新区间的时候要进行路径的压缩，压缩的过程中需要对权值进行更新，目的是使每个已知区间最大化。
https://blog.csdn.net/ling_wang/article/details/81515541

//带权并查集 更新父节点的同时更新权值
#include
using namespace std;

const int N = 200020;
int pre[N];
int cnt[N];//cnt[i]代表i到自己祖先的权值

int Find(int x){//路径压缩，更新父节点和权值
    if(x != pre[x]){
        int fa = pre[x];
        pre[x] = Find(pre[x]);
        //当合并祖先时，x到新祖先的权值等于x到旧祖先的权值加旧祖先到新祖先的权值（此处的cnt[x]还没更新到结点所以还是到旧祖先的权值）
        cnt[x] += cnt[fa];
    }
    return pre[x];
}

int main(){
    int n, m, x, y, w, s;
    while(scanf("%d%d", &n, &m) != EOF){
        s = 0;
        for(int i = 0; i <= n; i++){
            pre[i] = i;
            cnt[i] = 0;
        }
        while(m--){
            scanf("%d%d%d", &x, &y, &w);
            int fx = Find(x-1);//因为[a, b]中包含a，所以实际上是对(a, b]操作，即x = x-1
            int fy = Find(y);
            //cout << "fx = " << fx << " fy = " << fy << endl;
            if(fx == fy){//如果发现该区间的权值和之前得出的权值不等，s++
                if(cnt[x-1] + w != cnt[y])
                    s++;
            }
            /*
            在合并操作中，对我们需要更新cnt[fb]（由于fy成为fa的子节点），公式：cnt[fy] = cnt[x - 1] - cnt[y] + w
            - 更新cnt[fy]的目的是维护子树(fy)相对于父亲树(fx)之间的权值差。
            - cnt[y]保存结点y到结点fy之间的权值； cnt[x-1]保存结点x-1到结点fx之间的权值；w是结点x-1到结点y之间的权值
            - 所以cnt[fy]的值=从结点fa到结点x-1的权值(+cnt[x - 1])，加上从结点x到结点y的权值(+w)，最后减去结点fy到结点y的权值(-cnt[y])
            */
            else{
                pre[fy] = fx;
                //cout << "pre[fy] = " << pre[fy] << endl;
                cnt[fy] = cnt[x-1] + w - cnt[y];
                //cout << "cnt[fy] = " << cnt[fy] << endl;
            }
        }
        printf("%d\n", s);
    }
    return 0;
}

二.种类并查集

注意：权值的累加变成累加结果%mod ，，，

例题：poj 1182 食物链

http://poj.org/problem?id=1182
题意：
给出N个动物所构成的食物链关系；N个动物分为三类：A,B,C，这三类动物的食物链构成了有趣的环形，A吃B， B吃C，C吃A
有几个种类就模几，这里是%3

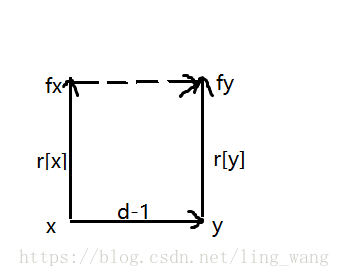
r[x] 表示x与祖先的关系
这里有三种关系：
r[x] = 0 表示x与祖先fx同类
r[x] = 1 表示x吃祖先fx
r[x] = 2 表示x被祖先fx吃

剩下的也是用向量来解决~

#include
#include
using namespace std;

const int N = 100000+10;
int pre[N], r[N];

int Find(int x){
    int fa = pre[x];
    if(x != pre[x]){
        pre[x] = Find(pre[x]);
        r[x] = (r[x] + r[fa]) % 3;
    }
    return pre[x];
}

int main(){
    int i, n, m, d, x, y, s, fx, fy;
    scanf("%d%d", &n, &m);
    s = 0;
    for(i = 0; i <= n; i++){
        pre[i] = i;
        r[i] = 0;
    }
    while(m--){
        scanf("%d%d%d", &d, &x, &y);
        fx = Find(x); fy = Find(y);
        if(x > n || y > n || (x == y && d == 2)){
            s++;
            //cout << "s1 = " << s <
        }
        else if(fx == fy && (r[x] - r[y] + 3)%3 != d-1){
            s++;
            // cout << "s2 = " << s<< endl;
        }
        else if(fx != fy){
            pre[fx] = fy;
            r[fx] = (3-r[x] + d-1 + r[y]) % 3;
        }
    }
    printf("%d\n", s);
    return 0;
}