hdu - 6350

Topic

题目链接
Always Online

Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 208 Accepted Submission(s): 66

Problem Description
Wayne is an administrator of some metropolitan area network. The network he managed can be formed into a simple connected graph with n vertices and m edges, which means the graph does not contain any self-loop and there is at most one edge and at least one path between every two vertices. Furthermore, the network also meets the condition there are at most two non-intersect paths, which share no common edges, between every two vertices.

Wayne knows the bandwidth of each edge in that network but it is not enough for him. He needs plenty of statistic data to display, for example, he wants to know what the maximum data rate between every two vertices is. For the sake of clarity, vertices in that are numbered from 1 to n and the maximum bits each edge could transmit per second will be given. Your task is assisting him to calculate the value of the following formula:

∑1≤s

Intention

给出一个无向图，不存在自环，两点间最多有一条边，两点间至少有一条路径，至多两条不相交路径。给出每条边以及两边之间的容量，询问

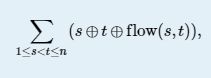
Solution

• 考虑这个图，其实就是一个仙人掌，大概就是长这样：
• 
• 考虑如果是一棵树，那么两点最大流，即最小割就是两点路径上最小的边权
• 考虑仙人掌，意识流一下，对于两个点的最小割可能要割两条边，而这两条边一定在同一个环内，且环内最小边一定会被割掉
• 那么就可以预处理先把每个环内最小边删除并将权值加到这个环的每一条边上，此时将变成一棵树
• 对于一棵树，我们将所有边按权值从大到小枚举，通过并查集，按位记录点的贡献，对于每条边，再算出该边的贡献，累加即是答案
  

一开始用vector去跑图竟然爆栈了，大概是因为边太多的原因，本地扩栈不会爆RE，所以改了std的dfs写法，解决了segment fault 的问题，然后TLE了，将位统计的64改成32就ac了

Code

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const ll LINF = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const double PI = acos(-1.0);
const double eps = 1e-10;
const int maxn = 4e5 + 7;
#define REP(i, j, k) for(int i = j;i <= k; ++i)
#define PER(i, j, k) for(int i = j;i >= k; --i)
int t, n, m, vis[maxn], dep[maxn], prt[maxn], bit[maxn][40], num[maxn], tot, fae[maxn], f[maxn];
int e[maxn], g[maxn], nt[maxn];
struct G
{
    int u, v, w, id;
    G(){}
    G(int u, int v, int w, int id):u(u), v(v), w(w), id(id){}
    bool operator < (const G & b) const {return w > b.w;}
} edge[maxn];
int get_prt(int a)
{
    return prt[a] = (prt[a] == a) ? a : get_prt(prt[a]);
}
ll Union (int a, int b, int w)
{
    int fa = get_prt(a), fb = get_prt(b);
    ll res = 0;
    if(fa == fb) return res;
    REP(i, 0, 31)
    {
        if(!(w & (1ll << i)))
        {
            res += 1ll * bit[fa][i] * (num[fb] - bit[fb][i]) * (1ll << i);
            res += 1ll * (num[fa] - bit[fa][i]) * bit[fb][i] * (1ll << i);
        }
        else
        {
            res += 1ll * bit[fa][i] * bit[fb][i] * (1ll << i);
            res += 1ll * (num[fa] - bit[fa][i]) * (num[fb] - bit[fb][i]) * (1ll << i);
        }
    }
    prt[fb] = fa;
    num[fa] += num[fb];
    REP(i, 0, 31)
    {
        bit[fa][i] += bit[fb][i];
    }
    return res;
}
void init()
{
    memset(dep, 0, sizeof(dep));
    memset(vis, 0, sizeof(vis));
    memset(fae, 0, sizeof(fae));
    memset(bit, 0, sizeof(bit));
    memset(f, 0, sizeof(f));
    memset(nt, 0, sizeof(nt));
    memset(g, 0, sizeof(g));
}
void adde(int u, int v)
{
    e[++tot] = v; nt[tot] = g[u]; g[u] = tot;
    e[++tot] = u; nt[tot] = g[v]; g[v] = tot;
}
void dfs(int u, int pre)
{
    f[u] = pre; dep[u] = ++tot;
    for(int i = g[u];i;i = nt[i])
    {
        if(e[i] == pre) continue;
        if(!dep[e[i]]) fae[e[i]] = i >> 1, dfs(e[i], u);
        else if(dep[e[i]] < dep[u])
        {
            int v = u;
            vector<int> vec; vec.push_back(i >> 1);
            while(v != e[i])
                vec.push_back(fae[v]), v = f[v];
            int Min = 1e9 + 1, pos = 0;
            REP(j, 0, vec.size() - 1)
            {
                if(edge[vec[j]].w < Min)
                    Min = edge[vec[j]].w, pos = j;
            }
            vis[vec[pos]] = 1;
            REP(j, 0, vec.size() - 1)
            {
                if(j != pos) edge[vec[j]].w += edge[vec[pos]].w;
            }
        }
    }
}
int main()
{
#ifdef DEBUG
    freopen("input.txt", "r", stdin);
#endif // DEBUG
    scanf("%d", &t);
    while(t--)
    {
        init();
        scanf("%d %d", &n, &m);
        REP(i, 1, n)
        {
            int _i = i, cnt = 0;
            while(_i) bit[i][cnt++] = _i % 2, _i /= 2;
            num[i] = 1;
            prt[i] = i;
        }
        int u, v, w;
        tot = 1;
        REP(i, 1, m) scanf("%d %d %d", &u, &v, &w), edge[i] = G(u, v, w, i), adde(u, v);
        dfs(1, 0);
        sort(edge + 1, edge + m + 1);
        ll ans = 0;
        REP(i, 1, m)
        {
            if(vis[edge[i].id]) continue;
            int u = edge[i].u, v = edge[i].v, w = edge[i].w;
            //cout<
            ans += Union(u, v, w);
        }
        printf("%llu\n", ans);
    }
    return 0;
}